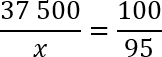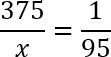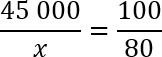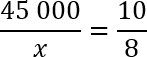Как посчитать проценты крест накрест
Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
Это простейшее линейное уравнение. Выразим из него переменную x :
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Как находить проценты от числа
Основные определения
Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.
Чтобы узнать, как перевести проценты в десятичную дробь, нужно убрать знак % и разделить известное на 100. Например, 18% — это 18 : 100 = 0,18.
А если нужно перевести натуральное число или десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%.
Выразить дробь в процентах просто. Для перевода сначала превратим ее в десятичную дробь, а далее используем предыдущее правило и переведём десятичную дробь в проценты.
Проценты: правила
Рассмотрим четыре известных способа поиска процентов.
Занимайтесь математикой в удовольствие вместе с нашими преподавателями на онлайн-курсах по математике для детей и подростков!
Нахождение одного процента от числа
Найти процент от числа можно несколькими способами.
Первый способ
Найдем, чему равен 1%.
Умножим полученное значение на количество искомых процентов.
Пример: найти 12% от числа 48.
Второй способ
Переведем проценты в десятичную дробь.
Умножим число на полученную десятичную дробь.
Давайте снова найдем 12% от 48, но другим способом.
Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?
Как решаем:
250 : 100 = 2,5 — это 1% от стоимости шоколада,
значит, 2,5 × 15 = 37,5 — это 15%.
Ответ: выгоднее воспользоваться скидкой 15%.
Составление пропорции
Равенство двух отношений называют пропорцией.
a : b = c : d или a/b = c/d
Читается: а относится к b так, как с относится к d. Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение.
Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?
Как решаем:
Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию:
1390 руб. = 100%
x руб. = 14%
Перемножим крест-накрест и найдем x:
x = 1390 × 14 : 100
x = 194,6
Ответ: выгода по скидке составила 194,6 рубля.
Соотношения чисел
Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.
| Процент | Дробь | Как найти % от числа a |
|---|---|---|
| 10% | 1/10 | a : 10 |
| 20% | 1/5 | a : 5 |
| 25% | 1/4 | a : 4 |
| 50% | 1/2 | a : 2 |
| 75% | 3/4 | a : 4 × 3 |
Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?
Как решаем:
значит, нужно заплатить 75% от первоначальной цены.
75% — это 3/4 от числа, значит,
8500 : 4 × 3 = 6375 (рублей).
Ответ: средств хватит, так как пиджак стоит 6375 рублей.
Онлайн-калькулятор
Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:
Метод решения задач с процентами
Все соотношения и формулы, полученные для решения задач с процентами выводятся из пропорции
Данные задачи на проценты можно записать в виде следующих соотношений:
которые можно записать в виде пропорции
| все | = | 100% |
| часть | часть в % |
Используя эту пропорцию можно получить формулы для решения основных типов задач на проценты.
Примеры решения задач на проценты
30 соответствует 100% x соответствует 15%
решим полученное уравнение
| x = | 30 · 15% | = 4.5 |
| 100% |
Ответ: 15% от 30 равно 4.5.
20 соответствует 100% 35 соответствует x
решим полученное уравнение
| x = | 35 · 100% | = 175% |
| 20 |
Ответ: 35 составляет 175% от 20.
x соответствует 100% 20 соответствует 5%
решим полученное уравнение
| x = | 20 · 100% | = 400 |
| 5% |
Ответ: 400.
При изучении процентов вам также будут полезны:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Вычисление процентов, или Повседневная математика
Вычисление процентов – несложная математическая операция, которая довольно часто встречается в повседневной жизни. Например, нужно посчитать, сколько человек экономит, используя дисконтную карту магазина или покупая товар на распродаже со скидкой, под какой процент берет кредит. Проценты можно посчитать при помощи калькулятора или пропорции, пригодится формула вычисления процентов и знание элементарных известных соотношений.
Что такое процент от числа
Вычисление процентов в школьной программе изучается классе в 5-м, если не раньше. Согласно определению, процент – это одна сотая часть числа. Термин появился в Древнем Риме и буквально переводится как «со ста». Первоначально идея вычислять проценты зародилась еще в Вавилоне. Параллельно в Древней Индии научились считать проценты при помощи пропорции.
Для того чтобы найти процент от числа, необходимо данное число поделить на 100. Очевидно, что 1 % от 100 равняется единице.
Вычисление процентов по формулам
Формула, позволяющая найти процент от числа, элементарна. Необходимо число поделить на 100, после чего умножить на нужный процент.
Например, нужно рассчитать 25 % от числа 300. Расчет по вышеуказанной формуле будет иметь вид: 300/100*25=75.
Расчеты при помощи пропорции
Умножение крест-накрест даст равенство: А*Х=В*100. Следовательно, Х=В*100/А.
Например, необходимо узнать, сколько процентов от 300 составляет число 75. Получается: 75*100/300=25 %.
Альтернативный метод вычислений
Если возникают сомнения в правильности проводимых расчетов, всегда можно проверить себя на калькуляторе, который сейчас есть в любом мобильном устройстве и на любом компьютере.
Решение уравнений с пропорцией
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию. Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или, как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке «Пропорции». В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Произведение крайних членов пропорции равно произведению средних.
Вернемся к нашему уравнению. Решим его, использую правило пропорции. Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и решим уравнение до конца. В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Если в члене пропорции присутствуют знаки « + » или « − », обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда будете использовать правило пропорции.
После заключения в скобки члена пропорции « (2 − x) » используем правило пропорции для дальнейшего решения.
Теперь раскроем скобки с помощью правила раскрытия скобок.
Из урока «Решение линейных уравнений» используем правило переноса и правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение, в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления « : » можно заменить на дробную черту.