Как посчитать погрешность измерения прибора

Расчет погрешности измерений

3.1 Среднеарифметическая погрешность.Как уже отмечалось раньше, измерения принципиально не могут быть абсолютно точными. Поэтому в ходе измерения возникает задача об определении интервала, в котором вероятнее всего находится истинное значение измеряемой величины. Такой интервал указывают в виде абсолютной ошибки измерения.

Если предположить, что грубые промахи в измерениях устранены, а систематические ошибки сведены к минимуму тщательной настройкой приборов и всей установки и не являются определяющими, то результаты измерений будут, в основном, содержать только случайные погрешности, которые являются знакопеременными величинами. Поэтому, если проведено несколько повторных измерений одной и той же величины, то наиболее вероятным значением измеряемой величины является ее среднеарифметическое значение:

(1)

Погрешностью или абсолютной ошибкой отдельного измерения называют разность между значением, полученным в данном измерении, и среднеарифметическим значением измеряемой величины:

(2)

Средней абсолютной ошибкойназывается среднеарифметическое модулей абсолютных ошибок отдельных измерений:

(3)

При достаточно большом числе измерений случайные ошибки возникают с равной вероятностью как в сторону увеличения, так и в сторону уменьшения измеряемой величины, то есть можно считать, что истинное значение измеряемой величины заключено в интервале

(4)

Последнее неравенство обычно принято записывать как окончательный результат измерения следующим образом:

(5)

Относительная погрешность.Абсолютная ошибка определяет интервал наиболее вероятных значений измеряемой величины, но не характеризует степень точности произведенных измерений. Например, расстояние между населенными пунктами, измеренное с точностью до нескольких метров, можно отнести к весьма точным измерениям, в то время как измерение диаметра проволоки с точностью до 1 мм, в большинстве случаев будет являться весьма приближенным измерением.

Степень точности проведенных измерений характеризует относительная погрешность.

Средней относительной погрешностьюили просто относительной ошибкой измерения называется отношение средней абсолютной ошибки измерения к среднему значению измеряемой величины:

(6)

или выраженная в процентах

(7)

Относительная ошибка является безразмерной величиной и обычно выражается в процентах.

3.2 Погрешность метода или приборная погрешность.Среднеарифметическое значение измеряемой величины тем ближе к истинному, чем больше проведено измерений, при этом абсолютная погрешность измерения с увеличением их числа стремится к значению, которое определяется методом измерения и техническими характеристиками используемых приборов.

Погрешность методаили приборную погрешность можно рассчитать по одноразовому измерению, зная класс точности прибора или другие данные технического паспорта прибора, в котором указывается либо класс точности прибора, либо его абсолютная или относительная погрешность измерения.

Класс точностиприбора выражает в процентах номинальную относительную ошибку прибора, то есть относительную ошибку измерения, когда измеряемая величина равна предельному для данного прибора значению

(8)

Класс точности указывается на шкале прибора цифрой, обведенной кружочком. Согласно ГОСТу все электроизмерительные приборы разделяются на 8 классов: 0,05; 0,1; 0,2; 0,5; 1.0 1,5; 2,5; 4,0.

Абсолютная погрешность прибора равна предельному для данного прибора значению измеряемой величины, умноженному на класс точности (К) и разделен­ному на 100:

(9)

Абсолютная погрешность прибора не зависит от значения измеряемой величины.

Относительная погрешность прибора (по определению):

(10)

При работе с простыми приборами (линейка, мензурка и т.п.), классы точности и погрешности которых не определены техническими характеристиками, абсолютную погрешность прямых измерений принимают равной половине цены деления данного прибора. (Ценой деления называют значение измеряемой величины при показаниях прибора в одно деление).

Приборную погрешность косвенных измеренийможно рассчитать, используя правила приближенных вычислений. В основе вычисления погрешности косвенных измерений лежат два условия (предположения):

1. Абсолютные ошибки измерений всегда очень малы по сравнению с измеряемыми величинами. Поэтому абсолютные ошибки (в теории) можно рассматривать как бесконечно малые приращения измеряемых величин, и они могут быть заменены соответствующими дифференциалами.

2. Если физическая величина, которую определяют косвенным путем, является функцией одной или нескольких непосредственно измеряемых величин, то абсолютная ошибка функции, обусловленная бесконечно малыми приращениями, является также бесконечно малой величиной.

При указанных допущениях абсолютную и относительную погрешность можно рассчитать, используя известные выражения из теории дифференциального исчисления функций многих переменных:

	(11)
	(12)

	(13)
	(14)

Таким образом: а) абсолютная ошибка косвенного метода измерения равна сумме модулей произведений частных производных функции измерения и соответствующих абсолютных ошибок прямых измерений; б) относительная ошибка косвенного метода измерения равна сумме модулей дифференциалов от логарифма натурального функции измерения, определяемой расчетной формулой.

Выражения (13) и (14) позволяют рассчитать абсолютные и относительные погрешности по одноразовому измерению. Заметим, что для сокращения расчетов по указанным формулам достаточно рассчитать одну из погрешностей (абсолютную или относительную), а другую рассчитать, используя простую связь между ними:

(15)

На практике чаще пользуются формулой (13), так как при логарифмировании расчетной формулы произведения различных величин преобразуются в соответствующие суммы, а степенные и показательные функции преобразуются в произведения, что намного упрощает процесс дифференцирования.

Для практического руководства по расчету погрешности косвенного метода измерения можно пользоваться следующим правилом:

Чтобы вычислить относительную ошибку косвенного метода измерения, нужно:

1. Определить абсолютные ошибки (приборные или средние) прямых измерений.

2. Прологарифмировать расчетную (рабочую) формулу.

3. Принимая величины прямых измерений за независимые переменные, найти полный дифференциал от полученного выражения.

4. Сложить все частные дифференциалы по абсолютной величине, заменив в них дифференциалы переменных соответствующими абсолютными ошибками прямых измерений.

5. Используя полученное выражение, рассчитать относительную погрешность.

6. По формуле (15) рассчитать абсолютную ошибку.

Например, плотность тела цилиндрической формы вычисляется по формуле:

(16)

Получим формулу для расчета погрешностей.

1. Исходя из используемого оборудования, определяем абсолютные погрешности измерения массы, диаметра и высоты цилиндра (∆m, ∆D, ∆h соответственно).

2. Логарифмируем выражение (16):

4. Заменяя дифференциал независимых переменных на абсолютные ошибки и складывая модули частных приращений, получаем:

5. Используя численные значения m, D, h, D, m, h, рассчитываем Е.

6. Вычисляем абсолютную ошибку

где r рассчитано по формуле (16).

Предлагаем самим убедиться, что в случае полого цилиндра или трубки с внутренним диаметром D₁ и внешним диаметром D₂

К расчету ошибки метода измерения (прямого или косвенного) приходится прибегать в случаях, когда многократные измерения либо невозможно провести в одних и тех же условиях, либо они занимают много времени.

Если определение погрешности измерения является принципиальной задачей, то обычно измерения проводят многократно и вычисляют и среднеарифметическую погрешность и погрешность метода (приборную погрешность). В окончательном результате указывают большую из них.

О точности вычислений

Ошибка результата определяется не только неточностями измерений но и неточностями вычислений. Вычисления необходимо проводить так, чтобы их ошибка была на порядок меньше ошибки результата измерений. Для этого вспомним правила математического действия с приближёнными числами.

Правила округления чисел

При округлении оставляют лишь верные знаки, остальные отбрасываются.

1. Округление достигается простым отбрасыванием цифр, если первая из отбрасываемых цифр меньше, чем 5.

2. Если первая из отбрасываемых цифр больше, чем 5, то последняя цифра увеличивается на единицу. Последняя цифра увеличивается также и в том случае, когда первая из отбрасываемых цифр 5, а за ней есть одна или несколько цифр, отличных от нуля.

Например, различные округления числа 35,856 будут: 35,9; 36.

3. Если отбрасываемая цифра 5, а за ней нет значащих цифр, то округление производится на ближайшее чётное число, то есть, последняя сохраняемая цифра остаётся неизменной, если она чётная и увеличивается на единицу, если она нечётная.

Например, 0,435 округляем до 0,44; 0,365 округляем до 0,36.

Источник

Погрешность измерений

Неотъемлемой частью любого измерения является погрешность измерений. С развитием приборостроения и методик измерений человечество стремиться снизить влияние данного явления на конечный результат измерений. Предлагаю более детально разобраться в вопросе, что же это такое погрешность измерений.

Погрешность измерения – это отклонение результата измерения от истинного значения измеряемой величины. Погрешность измерений представляет собой сумму погрешностей, каждая из которых имеет свою причину.

По форме числового выражения погрешности измерений подразделяются на абсолютные и относительные

Абсолютная погрешность – это погрешность, выраженная в единицах измеряемой величины. Она определяется выражением.

(1.2), где X — результат измерения; Х₀ — истинное значение этой величины.

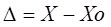
Поскольку истинное значение измеряемой величины остается неизвестным, на практике пользуются лишь приближенной оценкой абсолютной погрешности измерения, определяемой выражением

(1.3), где Х_д — действительное значение этой измеряемой величины, которое с погрешностью ее определения принимают за истинное значение.

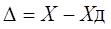
Относительная погрешность – это отношение абсолютной погрешности измерения к действительному значению измеряемой величины:

(1.4)

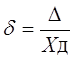
По закономерности появления погрешности измерения подразделяются на систематические, прогрессирующие, и случайные .

Систематическая погрешность – это погрешность измерения, остающаяся постоянной или закономерно изменяющейся при повторных измерениях одной и той же величины.

Прогрессирующая погрешность – это непредсказуемая погрешность, медленно меняющаяся во времени.

Систематические и прогрессирующие погрешности средств измерений вызываются:

Систематическая погрешность остается постоянной или закономерно изменяющейся при многократных измерениях одной и той же величины. Особенность систематической погрешности состоит в том, что она может быть полностью устранена введением поправок. Особенностью прогрессирующих погрешностей является то, что они могут быть скорректированы только в данный момент времени. Они требуют непрерывной коррекции.

Случайная погрешность – это погрешность измерения изменяется случайным образом. При повторных измерениях одной и той же величины. Случайные погрешности можно обнаружить только при многократных измерениях. В отличии от систематических погрешностей случайные нельзя устранить из результатов измерений.

По происхождению различают инструментальные и методические погрешности средств измерений.

Инструментальные погрешности — это погрешности, вызываемые особенностями свойств средств измерений. Они возникают вследствие недостаточно высокого качества элементов средств измерений. К данным погрешностям можно отнести изготовление и сборку элементов средств измерений; погрешности из-за трения в механизме прибора, недостаточной жесткости его элементов и деталей и др. Подчеркнем, что инструментальная погрешность индивидуальна для каждого средства измерений.

Методическая погрешность — это погрешность средства измерения, возникающая из-за несовершенства метода измерения, неточности соотношения, используемого для оценки измеряемой величины.

Погрешности средств измерений.

Абсолютная погрешность меры – это разность между номинальным ее значением и истинным (действительным) значением воспроизводимой ею величины:

(1.5), где X_н – номинальное значение меры; Х_д – действительное значение меры

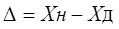
Абсолютная погрешность измерительного прибора – это разность между показанием прибора и истинным (действительным) значением измеряемой величины:

(1.6), где X_п – показания прибора; Х_д – действительное значение измеряемой величины.

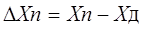
Относительная погрешность меры или измерительного прибора – это отношение абсолютной погрешности меры или измерительного прибора к истинному

(действительному) значению воспроизводимой или измеряемой величины. Относительная погрешность меры или измерительного прибора может быть выражена в ( % ).

(1.7)

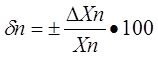
Приведенная погрешность измерительного прибора – отношение погрешности измерительного прибора к нормирующему значению. Нормирующие значение XN – это условно принятое значение, равное или верхнему пределу измерений, или диапазону измерений, или длине шкалы. Приведенная погрешность обычно выражается в ( % ).

(1.8)

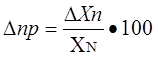
Основная – это погрешность средства измерений, используемого в нормальных условиях, которые обычно определены в нормативно-технических документах на данное средство измерений.

Дополнительная – это изменение погрешности средства измерений вследствии отклонения влияющих величин от нормальных значений.

Статическая – это погрешность средства измерений, используемого для измерения постоянной величины. Если измеряемая величина является функцией времени, то вследствие инерционности средств измерений возникает составляющая общей погрешности, называется динамической погрешностью средств измерений.

Также существуют систематические и случайные погрешности средств измерений они аналогичны с такими же погрешностями измерений.

Факторы влияющие на погрешность измерений.

Погрешности возникают по разным причинам: это могут быть ошибки экспериментатора или ошибки из-за применения прибора не по назначению и т.д. Существует ряд понятий которые определяют факторы влияющие на погрешность измерений

Вариация показаний прибора – это наибольшая разность показаний полученных при прямом и обратном ходе при одном и том же действительном значении измеряемой величины и неизменных внешних условиях.

Класс точности прибора – это обобщенная характеристика средств измерений (прибора), определяемая пределами допускаемых основной и дополнительных погрешностей, а также другими свойствами средств измерений, влияющих на точность, значение которой устанавливаются на отдельные виды средств измерений.

Классы точности прибора устанавливают при выпуске, градуируя его по образцовому прибору в нормальных условиях.

Прецизионность — показывает, как точно или отчетливо можно произвести отсчет. Она определяется, тем насколько близки друг к другу результаты двух идентичных измерений.

Разрешение прибора — это наименьшее изменение измеряемого значения, на которое прибор будет реагировать.

Диапазон прибора — определяется минимальным и максимальным значением входного сигнала, для которого он предназначен.

Полоса пропускания прибора — это разность между минимальной и максимальной частотой, для которых он предназначен.

Чувствительность прибора — определяется, как отношение выходного сигнала или показания прибора к входному сигналу или измеряемой величине.

Шумы — любой сигнал не несущий полезной информации.

Источник

Погрешности измерений

Общие сведения об измерениях. Погрешности измерений и средств измерений

Общие сведения об измерениях

Измерение – нахождение значения физической величины опытным путем с помощью специальных технических средств. Под измерением понимается процесс экспериментального сравнения данной физической величины с однородной физической величиной, значение которой принято за единицу.

Мера – средство измерений, предназначенное для воспроизведения физической величины заданного размера.

Измерительный прибор – средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем. Измерительные приборы классифицируются по различным признакам. Например, измерительные приборы можно построить на основе аналоговой схемотехники или цифровой. Соответственно их делят на аналоговые и цифровые. Ряд приборов, выпускаемых промышленностью, допускают только отсчитывание показаний. Эти приборы называются показывающими. Измерительные приборы, в которых предусмотрена регистрация показаний, носят название регистрирующих.

Погрешности измерений

Погрешность является одной из основных характеристик средств измерений.

Под погрешностью электроизмерительных приборов, измерительных преобразователей и измерительных систем понимается отклонение их выходного сигнала от истинного значения входного сигнала.

Абсолютная погрешность Δ_a прибора есть разность между показанием прибора а_х и истинным значением а измеряемой величины, т.е.

Абсолютная погрешность, взятая с обратным знаком, называется поправкой.

Относительная погрешность δ представляет собой отношение абсолютной погрешности к истинному значению измеряемой величины. Относительная погрешность, обычно выражаемая в процентах, равна

Приведенная погрешность γ_П есть выраженное в процентах отношение абсолютной погрешности Δ_a к нормирующему значению а_пр

Нормирующее значение – условно принятое значение, могущее быть равным конечному значению диапазона измерений (предельному значению шкалы прибора).

Погрешности средств измерений

Класс точности прибора указывают просто числом предпочтительного рода, например, 0,05. Это используют для измерительных приборов, у которых предел допускаемой приведенной погрешности постоянен на всех отметках рабочей части его шкалы (присутствует только аддитивная погрешность). Таким способом обозначают классы точности вольтметров, амперметров, ваттметров и большинства других однопредельных и многопредельных приборов с равномерной шкалой.

Класс точности прибора (например, амперметра) дается выражением

При установлении классов точности приборов нормируется приведенная погрешность, а не относительная. Причина этого заключается в том, что относительная погрешность по мере уменьшения значений измеряемой величины увеличивается.

По ГОСТ 8.401-80 в качестве значений класса точности прибора используется отвлеченное положительное число из ряда:

В интервале от 1 до 100 можно использовать в качестве значений класса точности числа:

(α = 0) 1; 1,5; 2; 2,5; 4; 5; 6;

(α = 1) 10; 15; 20; 25; 40; 50; 60.

Т.е. четырнадцать чисел 1; 1,5; 2; 2,5; 4; 5; 6; 10; 15; 20; 25; 40; 50; 60.

Необходимо отметить, классы точности от 6,0 и выше считаются очень низкими.

Примеры решения задач

Задача №1

Определить для вольтметра с пределом измерения 30 В класса точности 0,5 относительную погрешность для точек 5, 10, 15, 20, 25 и 30 В и наибольшую абсолютную погрешность прибора.

Решение

Приведенная погрешность (выраженное в процентах отношение абсолютной погрешности к нормирующему значению)

постоянна и равна классу точности прибора.

Относительная погрешность однократного измерения (выраженное в процентах отношение абсолютной погрешности к истинному значению измеряемой величины)

уменьшается к значению класса точности прибора с ростом измеренного значения к предельному значению шкалы прибора.

Абсолютная погрешность однократного измерения

постоянна на всех отметках рабочей части шкалы прибора.

По условию задачи: U_изм = U_i = 5, 10, 15, 20, 25 и 30 В – измеренное значение электрической величины; U_пр = 30 В – предел шкалы вольтметра.

Источник