Как посчитать площадь сегмента круга

Как посчитать площадь сегмента круга

Сегмент круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Сегмент

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Параметры сегмента по хорде и высоте

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Источник

Нахождение площади сегмента круга

В данной публикации мы рассмотрим определение сегмента круга и формулы, с помощью которых можно вычислить его площадь (через радиус и центральный угол кругового сектора). Также разберем примеры решения задач для демонстрации практического применения формул.

Определение сегмента круга

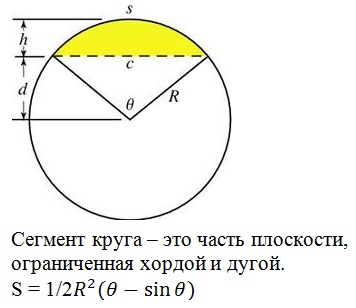
Сегмент круга – это часть круга, которая ограничена дугой окружности и ее хордой.

Хорда – это часть прямой (секущей), которая пересекает круг. Концы хорды соединяются с центром круга, в результате чего образуется равнобедренный треугольник, боковые стороны которого являются радиусом окружности. Если к этом треугольнику добавить сегмент, получится сектор.

Формулы нахождения площади кругового сегмента

Через радиус и центральный угол в градусах

α° – угол в градусах.

Через радиус и угол сектора в радианах

α_рад – угол в радианах.

Примеры задачи

Задание 1
Найдите площадь сегмента круга, если его радиус равен 8 см, а центральный угол сектора, стягивающего сегмент, составляет 45 градусов.

Решение
Воспользуемся первой формулой, подставив в нее известные значения:

Решение
В данном случае мы можем получить радиус из формулы, в которой задействован угол в радианах:

Источник

Выполняя инженерные расчёты при проектировании различных объектов строительства, создании роботов, автоматизированных систем, станков, машин, самолётов, ракет, современных средств вооружения часто бывает необходимо найти площадь сектора круга.

Геометрия помогает при этом решать задачи на нахождение центра тяжести (центр масс), вычислять его координаты для плоских пластин, имеющих, в частности, форму правильного многоугольника.

Измерять и вычислять величины считается базовым умением. Оно включено в первую часть профильной программы выпускного экзамена ЕГЭ и ОГЭ по математике.

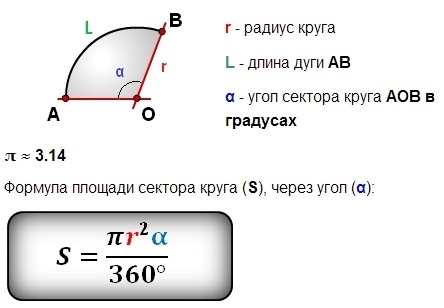
Сектор круга

Существует несколько определений, каждое из которых отличается только формулировкой, не меняющей подход к рассмотрению понятия:

Часть плоскости, ограниченная центральным углом и соответствующей дугой окружности.

Часть круга, заключённая между двумя радиусами.

Часто эту формулировку заменяют похожей, описывающей построение непосредственно: часть круга, лежащего внутри соответствующего центрального угла.

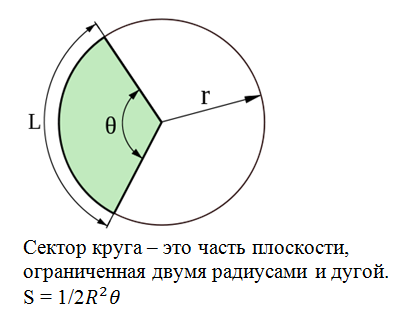
Площадь сектора круга через радиус и длину дуги

Пусть известны радиус круга R, длина дуги l. Как в этом случае определить площадь сектора, стягиваемого данной дугой?

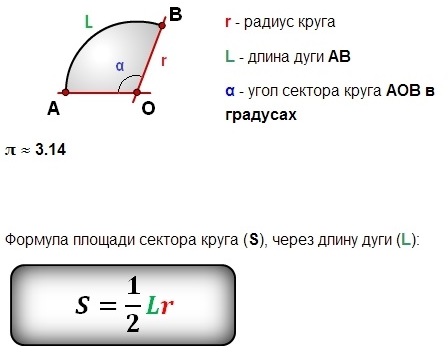
Для ответа на вопрос понадобится формула нахождения длины окружности:

Определение, представленное через третью формулировку, даёт возможность соотнести численные величины понятий: сектор и круг, дуга и окружность, центральный и полный углы.

После сокращения дроби получают формулу:

Примеры решения задач

Задача №1

Найти площадь сектора круга радиусом 2 см, имеющего длину дуги 4 см.

Подставляя имеющиеся величины в формулу, получаем:

Задача №2

Подставив известные данные в формулу, получим:

Тот же результат получился бы при первоначальной работе в «общем виде»:

Площадь сектора круга через радиус и угол сектора

Если известна градусная мера центрального угла (n°), то, находя отношение её к полному кругу (к 360º), также умножают результат на площадь круга:

Задача №3

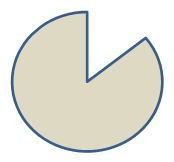
Чему равна площадь фигуры, изображённой на рисунке?

Центральный угол изображённого сектора равен

Подставляя в формулу величины, несложно получить искомый результат:

Также аналогичным образом решаются обратные задачи.

Площадь сектора круга через угол сектора в радианах

Пусть центральный угол задан своей радианной мерой. Учитывая, что

несложно получить искомую формулу:

Задача №4

Чему равен центральный угол сектора в радианах (рад.), если его площадь равна 32, а радиус – 4?

Выразив α, затем подставив числовые данные, легко получить результат:

Благодаря этой формуле, несложно доказать, что площади двух секторов с равными центральными углами относятся как квадраты радиусов соответствующих окружностей:

С другой стороны, площадь части кольца находится из условия:

Сегмент круга

Существует два подхода к определению понятия:

Геометрическая фигура, являющаяся общей частью круга и полуплоскости, называется сегментом круга.

Часть плоскости, заключённая между хордой и окружностью.

Оба определения характеризуют один и тот же объект с разных сторон, выражая, по сути одно и то же.

Иногда проводится описательное построение. В этом случае второй вариант быстрее приводит к данному термину.

Площадь сегмента круга по хорде и высоте

Тогда можно приближённо считать, что

Погрешность такого вычисления уменьшается вместе с отношением

В частности, когда дуга содержит угол, меньший 50º, то есть,

погрешность оказывается менее 1%.

Более точной является формула для любого сегмента меньшего полукруга:

Точный расчёт производится, исходя из свойства нахождения сложной фигуры, являющейся суммой или разностью двух и более объектов.

Сегмент является частью сектора, к которому либо добавлен треугольник, содержащий центральный угол (для дуг больших 180º), либо убран (соответствующий центральный угол меньше 180º).

Отсюда следует, что

Задача №5

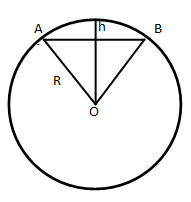
Вычислить стрелку и площадь сегмента, если центральный угол содержит 60º, а

Для нахождения стрелки достаточно из радиуса вычесть высоту треугольника AOB. Поскольку угол AOB по условию равен 60º, то треугольник AOB равносторонний. Поэтому его высота в √3/2 раз отличается от стороны (от радиуса).

Отсюда следует, что:

Площадь по первой формуле будет приблизительно равна

Применяя точную формулу и учитывая, что

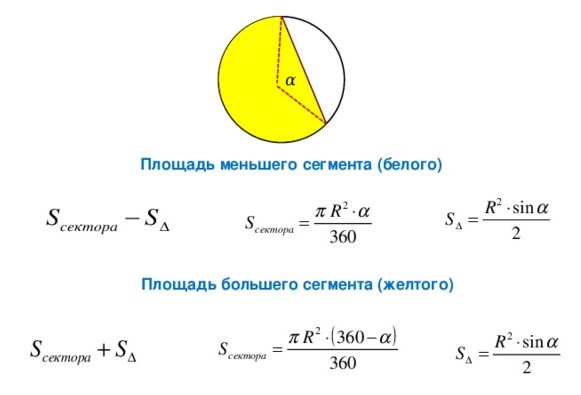
Площадь сегмента круга через синус угла

Рассматривая точную формулу, площадь треугольника можно находить, используя половину произведения сторон на синус угла между ними. А значит:

Многие вычисления помогает провести онлайн калькулятор. Достаточно ввести исходные данные и запросить результат.

Источник

Площадь круга и его частей. Длина окружности и ее дуг

Основные определения и свойства. Число π

Формулы для площади круга и его частей

Формулы для длины окружности и ее дуг

Площадь круга

Длина окружности

Длина дуги

Площадь сектора

Площадь сегмента

Основные определения и свойства

Часть окружности, расположенная между двумя точками окружности

Конечная часть плоскости, ограниченная окружностью

Часть круга, ограниченная двумя радиусами

Часть круга, ограниченная хордой

Выпуклый многоугольник, у которого все стороны равны и все углы равны

Около любого правильного многоугольника можно описать окружность

Фигура	Рисунок	Определения и свойства
Окружность
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами. Формулы для площади круга и его частей , где R – радиус круга, D – диаметр круга , если величина угла α выражена в радианах , если величина угла α выражена в градусах , если величина угла α выражена в радианах , если величина угла α выражена в градусах , где R – радиус круга, D – диаметр круга Числовая характеристика Рисунок Формула Площадь круга Площадь сектора , если величина угла α выражена в радианах , если величина угла α выражена в градусах Площадь сегмента , если величина угла α выражена в радианах , если величина угла α выражена в градусах Формулы для длины окружности и её дуг где R – радиус круга, D – диаметр круга если величина угла α выражена в радианах , если величина угла α выражена в градусах где R – радиус круга, D – диаметр круга Числовая характеристика Рисунок Формула Длина окружности Длина дуги если величина угла α выражена в радианах , если величина угла α выражена в градусах Площадь круга Длина окружности откуда вытекает формула для длины окружности радиуса R : Длина дуги Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла. В случае, когда величина α выражена в градусах, справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах, справедлива пропорция из которой вытекает равенство: Площадь сектора В случае, когда величина α выражена в градусах, справедлива пропорция из которой вытекает равенство: В случае, когда величина α выражена в радианах, справедлива пропорция из которой вытекает равенство: Площадь сегмента Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла. Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем В случае, когда величина α выражена в в радианах, получаем Источник Как посчитать площадь сегмента круга Круг — это часть плоскости, ограниченная окружностью. Центр данной окружности называется центром круга, а расстояние от центра до любой точки окружности — радиусом круга: O — центр круга, OA — радиус круга. Площадь круга Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга: где S — площадь круга, а r — радиус круга. Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2: D = 2r, значит r = D . 2 Следовательно, формула нахождения площади круга через диаметр будет выглядеть так: S = π( D ) 2 = π D 2 = π D 2 . 2 2 2 4 Сектор круга. Площадь сектора Сектор — это часть круга, ограниченная двумя радиусами и дугой. Два радиуса разделяют круг на два сектора: Чтобы найти площадь сектора, дуга которого содержит n°, надо площадь круга разделить на 360 и полученный результат умножить на n. Формула площади сектора: S = πr 2 · n = πr 2 n , 360 360 где S — площадь сектора. Выражение можно представить в виде произведения πr 2 n = n · πr · r , 360 180 2 где nπr — это длина дуги сектора. 180 Следовательно, площадь сектора равна длине дуги сектора, умноженной на половину радиуса: где S — это площадь сектора, s — длина дуги данного сектора, r — радиус круга. Сегмент. Площадь сегмента Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой. 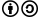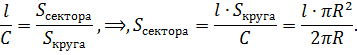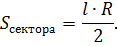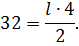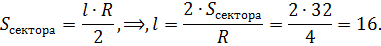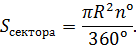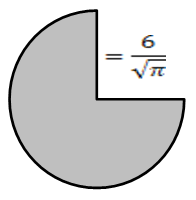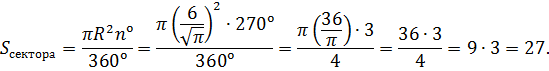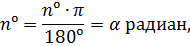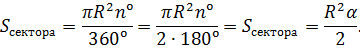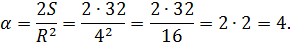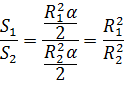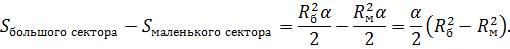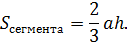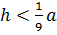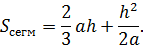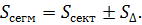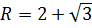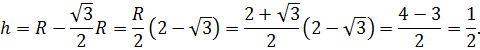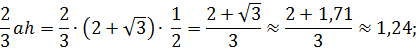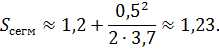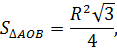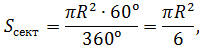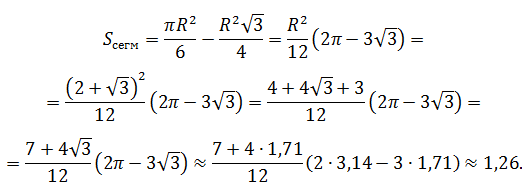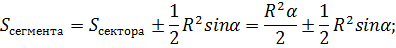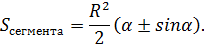Любая хорда делит круг на два сегмента: Площадь сегмента равна половине радиуса, умноженной на разность между дугой сегмента и половиной хорды двойной дуги. Площадь сегмента AMB будет вычисляться по формуле: где S — это площадь сегмента, r — радиус круга, s — длина дуги AB, а BC — длина половины хорды двойной дуги. Источник Читайте также:  Как похудеть на килограмм за ночь Вам также может понравиться Как почистить бумажный воздушный фильтр Как почистить воздушный фильтр своими руками Как почистить сахават запирович мвд дагестана биография Воскресный денек 26 марта в штабе 160-го гвардейского модуль нпб водителя что это Редкая штучка #2. Деактивизация НПБ переднего пассажира Как появились пряности на руси Приправы в Древней Руси. На Руси в виде приправ использовали Политика конфиденциальности Правообладателям Контакты