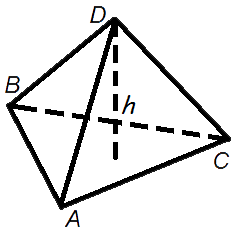
Как посчитать площадь объемной фигуры
Площадь фигур
Площадь фигуры является суммарной числовой характеристикой всех единичных квадратных элементов плоскости. В зависимости от размера фигур стороны квадрата единичного элемента могут быть равны 1 мм, см, м, дюйму, км и пр. S фигур могут измеряться в следующих единицах измерения: мм2, см2, м2, гектарах, квадратных километрах и пр.
Вычислить, найти площадь геометрических фигур
| Онлайн Расчеты и формулы площади для плоских фигур | |
| Площадь треугольника калькулятор нахождения площади треугольников | Площадь прямоугольного треугольника онлайн формула площади прямоугольного треугольника |
| Площадь равнобедренного треугольника найти площади равнобедренных треугольников | Площадь равностороннего треугольника вычислить площадь равностороннего треугольника |
| Площадь треугольника по формуле Герона площадь Герона, формула | Площадь квадрата чему равна площадь квадрата |
| Площадь прямоугольника как найти чему равна площадь прямоугольника | Площадь круга онлайн калькулятор площади круга через радиуса |
| Площадь ромба как найти площадь ромба через диагонали и т.д. | Площадь параллелограмма онлайн калькулятор для нахождения площади параллелограмма |
| Площадь трапеции площадь прямоугольной и равнобедренной трапеции | Площадь эллипса формула площади эллипса онлайн |
| Площадь кольца как вычислить площадь кольца онлайн | Площадь четырехугольника чему равна площадь четырехугольника, формула |
| Площадь сектора кольца подсчитать площади сектора кольца | Площадь сектора круга получить площадь сектора круга |
| Площадь сегмента круга решить площадь сегмента круга | |
| Онлайн Расчеты и формулы площади для объемных фигур | |
| Площадь шара калькулятор нахождения площадь поверхности сферы или шара | Площадь куба как найти чему равна площадь поверхности куба |
| Площадь цилиндра калькулятор для нахождения площади поверхности и основания цилиндра | Площадь пирамиды формулы расчета площади боковой поверхности и основания пирамиды |
| Площадь параллелепипеда калькулятор площади параллелепипеда прямоугольного и др. | Площадь конуса нахождение площади поверхностей конуса |
| Площадь усеченного конуса калькулятор нахождения площади поверхности усеченного конуса | Площадь тетраэдра площадь поверхности и грани тетраэдра |
| Площадь призмы калькулятор нахождения площади поверхности и боковой площади призмы | |
Площадь фигуры сложной формы может составляться из различных элементарных фигур: треугольников, квадратов, прямоугольников и пр. Общая площадь будет высчитываться путем суммирования площадей составляющих компонент.
Набор онлайн-калькуляторов страницы дает возможность оперативного вычисления не только S плоских фигур (квадрата, прямоугольника, круга, ромба, эллипса), но и площадей объемных фигур (куба, призмы, конуса, цилиндра, сферы, тетраэдра и пр.), являющихся совокупностью нескольких плоскостей.
Вычисление площадей фигур востребовано для решения различных задач:
— строительных;
— кадастровых;
— инженерных и пр.
Государство осуществляет кадастровый учет земельных участков, основным учитываемым параметром которых является площадь. Специалистами БТИ фиксируется общая и полезная жилая площадь квартир. В быту иногда нужно вычислять площадь ковра, натяжного потолка, площадь дачного участка и пр.
Вычисление объемов фигур
Радиус первого шара в \(5\) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?
Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в \(343\) раза больше объема второго шара?
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.
Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.
Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.
Базовая информация
Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?
Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.
Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.
Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.
Как посчитать площадь объемной фигуры
Объем куба равен кубу длины его грани.
Формула объема куба
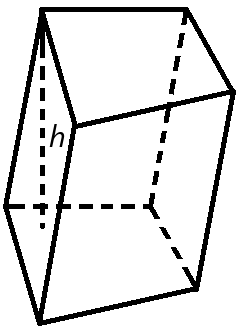
Объем призмы
Объем призмы равен произведению площади основания призмы, на высоту.
Формула объема призмы
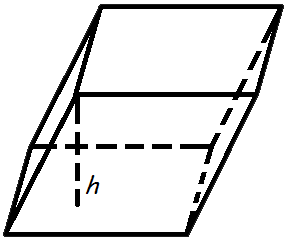
Объем параллелепипеда
Объем параллелепипеда равен произведению площади основания на высоту.
Формула объема параллелепипеда
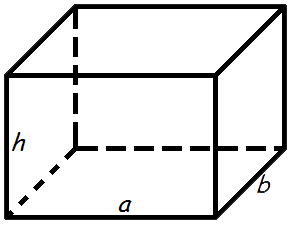
Объем прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
Формула объема прямоугольного параллелепипеда
Объем пирамиды
Объем пирамиды равен трети от произведения площади ее основания на высоту.
Формула объема пирамиды
Объем правильного тетраэдра
Формула объема правильного тетраэдра
Объем цилиндра
Объем цилиндра равен произведению площади его основания на высоту.
Объем конуса
Объем конуса равен трети от произведению площади его основания на высоту.
Формулы объема конуса
Объем шара
Объем шара равен четырем третим от его радиуса в кубе помноженого на число пи.
Формула объема шара
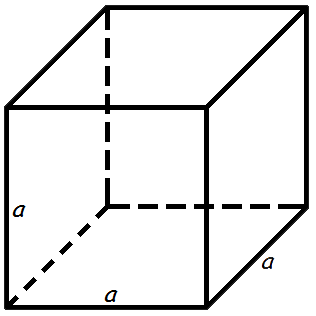
Площадь куба
Площадь поверхности куба равна квадрату длины его грани умноженному на шесть.
Формула площади куба
Площадь прямоугольного параллелепипеда
Формула площади поверхности прямоугольного параллелепипеда
Площадь цилиндра
Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.
Формула для вычисления площади боковой поверхности цилиндра
Площадь полной поверхности круглого цилиндра равна сумме площади боковой поверхности цилиндра и удвоенной площади основания.
Формула для вычисления площади полной поверхности цилиндра
Площади фигур (плоских и объемных)
Сначала мы рассмотрим площади плоских фигур.
Слышал ты что-нибудь про формулу Пика? Когда ее можно применять, а когда нельзя?
Сколько ты знаешь способов нахождения площади фигур на клетчатой бумаге? А их на самом деле три! И хотя задачу по нахождению площади фигур на клетчатой бумаге убрали из ЕГЭ, сам навык очень полезен для понимания планиметрии!
Во второй части мы рассмотрим как находить площади объемных фигур (призмы и пирамиды)
ПЛОЩАДИ ПЛОСКИХ ФИГУР
Способы нахождения площади фигур на клетчатой бумаге:
Способ 1. Считай клетки и применяй формулы
Удобен для стандартных фигур: треугольника, трапеции и т.д.
Способ 2. Дострой до прямоугольника и вычти лишнее
Очень удобен для сложных фигур, но и для простых неплох
Способ 3. Формула Пика
Работает только для многоугольников без дырок, все вершины которых попадают в узлы сетки.
Подсчитаем, сколько узлов попадает в нашу фигуру. Причём, отдельно посчитаем те узлы, которые попадают внутрь нашей фигуры, и отдельно – те, которые лежат на границе.
В примере на рисунке получилось \( Г = 22\) на границе и \( В = 32\) внутри.
Формула Пика. Делим границу пополам, прибавляем внутренности и вычитаем 1:\( S = Г/2 + В – 1 \)
Калькулятор вычисления объема и площади геометрических фигур
Весь осязаемый мир представляет собой объемные геометрические фигуры и их сочетания. Определение объемов и площадей поверхностей тел может понадобиться не только при решении школьных задач, но также в быту или профессиональной деятельности. Простые объемные тела разделяются на две категории.
Тела вращения
Первая категория — это тела вращения. Такие объемные фигуры образуются путем вращения плоской фигуры вокруг одной из сторон или путем движения образующей кривой вдоль направляющей. Наш каталог предлагает калькуляторы, при помощи которых можно рассчитать параметры следующих тел вращения.
Конус
Конус — фигура, которая создается путем вращения прямоугольного треугольника вокруг одного из катетов. Также конус формируется путем движения образующего луча вдоль направляющей окружности, при этом начало луча остается неподвижным. Для определения площади поверхности конуса используется простая формула:
где R — радиус основания, l — образующая конуса.
Для подсчета объема конической фигуры используется следующее соотношение:
где h — высота конуса.
Конусы широко встречаются в быту, производстве или науке. Например, коническую форму имеют вафельные рожки для мороженного, абажуры для светильников, пожарные ведра или воронки. В природе конус также распространен: горы, вулканы, сосновые шишки или шляпки грибов имеют форму данного тела.
Цилиндр
Цилиндр — тело вращения, которое образуется путем вращения прямоугольника вокруг одной из сторон. Также цилиндр формируется путем движения образующей прямой по направляющей кривой, которая в случае цилиндра может быть окружностью, эллипсом, параболой или гиперболой. Такие «экзотические» цилиндры носят соответствующие названия эллиптических, параболических и гиперболических фигур, однако в реальной жизни наибольшее распространение получил прямой круговой цилиндр. Для определения площади поверхности такого цилиндра используется формула:
где R — радиус основания, h — высота цилиндра.
Для вычисления объема цилиндра геометры применяют следующее соотношение:
Цилиндр легко встретить в реальной жизни: это и цистерны, и поршни двигателей, и колонны, и трубы газопроводов. Цилиндры широко используются в производстве, поэтому многим инженерам приходится вычислять площади поверхностей или объемы цилиндрических объектов.
Шар — тело вращения, созданное путем вращения круга около своей оси. Сфера — это поверхность, сформированная путем вращения окружности или полуокружности вокруг своей оси. Таким образом, шар — это пространство, ограниченное сферой. Площадь сферы вычисляется по формуле:
где R — радиус сферы.
Для подсчета объема шара используется следующее выражение:
Шар — идеальная фигура, поэтому в природе она встречается довольно часто. К примеру, сферическую форму принимают капли дождя, снежные комья, планеты, звезды, а также ягоды или кроны деревьев. В человеческой повседневности форму шара имеют спортивные мячи, пушечные ядра, подшипники или бусины.
Многогранники
Вторя категория — многогранники. Многогранник или полиэдр — это объемное тело, каждая грань которого является многоугольником. Существует огромное множество многогранников: к ним относятся призмы, пирамиды, параллелепипеды, а также платоновы тела — полиэдры, гранями которых являются правильные многоугольники. В нашем каталоге вы найдете инструменты для определения площадей поверхностей и объемов следующих многогранников.
Призма
Призма — это полиэдр, который состоит из двух n-угольных оснований, параллельных друг другу и n боковых граней, формирующих боковую поверхность призмы. Грань призмы — это всегда параллелограмм. Простыми словами, если в основании фигуры лежит квадрат, то призма считается четырехугольной, но при этом шестигранной: четыре грани составляют боковую поверхность, а две — поверхность оснований. Если в основании лежит пентагон — то призма пятиугольная и семигранная, а если додекагон — то фигура 12-угольная и 14-гранная. Если в основании призмы положить полигон, количество сторон которого стремится к бесконечности, то основание превратится в круг, а призма — в цилиндр. Для определения площади боковой поверхности призматической фигуры используется выражение:
где a — сторона параллелограмма, n — количество граней, h — его высота.
Площадь поверхности основания призмы зависит от многоугольника и в общем виде для правильных полигонов рассчитывается как:
So = n/4 × a 2 × ctg(pi/n),
где n — количество сторон фигуры, a — длина стороны.
Полная же площадь поверхности определяется как:
Объем призмы вычисляется по следующей формуле:
Призма — наиболее распространенный в человеческой повседневности полиэдр. Форму призмы имеет огромное число предметов вокруг вас: это системный блок компьютера, сабвуфер, стол, шкаф, комната и здание. Если выйти на улицу, то вы увидите царство призм. Именно поэтому инструмент для определения объемов и площадей поверхности призматических фигур всегда актуален.
Пирамида
Пирамида — это полиэдр, который составлен из n-угольного основания и n боковых граней, формирующих боковую поверхность пирамидальной фигуры. Грань пирамиды — это всегда треугольник. Вид полиэдра определяется в зависимости от того, какой полигон выступает в роли фундамента пирамиды. Следовательно, пирамиды бывают треугольные, четырехугольные, пятиугольные или n-угольные. Площадь боковой порвехности пирамиды рассчитывается согласно выражению:
где h — высота пирамиды, P — периметр полигона, лежащего в основании.
Площадь фундамента рассчитывается по общей формуле для любого правильного полигона:
So = n/4 × a 2 × ctg(pi/n),
где a — длина стороны, n — количество сторон.
Полная площадь поверхности пирамиды определяется как:
Для определения объема пирамиды используется формула:
где h — высота фигуры.
Пирамида — довольно распространенная фигура и широко используется в архитектуре. Всем известно о величественных пирамидах в Египте или колоссальных сооружениях в Южной Америке. Современные архитекторы также активно используют пирамиды при проектировании торговых комплексов, музеев или выставочных галерей. Кроме того, пирамидальные фигуры часто встречаются в производстве и машиностроении.
Параллелепипед
Параллелепипед — это гексаэдр с попарно параллельными гранями. Если ребра такого шестигранника равны, то параллелепипед превращается в куб. Параллелепипед — это частный случай прямой четырехугольной призмы, поэтому формулы для расчета площади и объема фигуры выводятся из соотношений для призмы с n = 4. Таким образом, для расчета площади поверхности гексаэдра используется формула:
где a, b — стороны основания параллелепипеда, h — высота фигуры.
Объем полиэдра определяется как:
Параллелепипед, так же как и призма, постоянно встречается в реальности. Форму такого гексаэдра имеет множество вещей вокруг нас: шлакоблоки, бетонные плиты, грузовые контейнеры или картонные коробки. Формулы для расчета атрибутов параллелепипеда, несомненно, пригодятся вам не только для решения школьных задач, но и в бытовых вопросах.
Примеры использования
Наш калькулятор позволяет рассчитать объем или площадь поверхности любого из заданных геометрических тел. Рассмотрим пару примеров.
Заливка бетона
К примеру, вы решили построить летний коттедж, а для каждого дома необходим фундамент. Вы выбрали плитный фундамент — монолитную плиту, которую заливают под всей площадью будущего жилища. Вам требуется узнать, сколько бетона понадобится для обустройства такого фундамента. Плитное основание представляет собой обычный параллелепипед, следовательно, вам понадобится определить объем шестигранника. Пусть вы хотите построить дом с размерами 6 на 9 метров, а толщина фундамента согласно техническим требованиям должна составлять 15 см. Приведем все параметры в одни единицы измерения и воспользуемся калькулятором для расчета объема параллелепипеда.
Таким образом, нам потребуется заказать 8,1 кубометров бетонной смеси.
Пошив мячей
Допустим, вы открыли производство по производству волейбольных мячей, и вам требуется узнать, сколько материала уходит на пошив одного мяча. Согласно данным из Википедии, стандартный волейбольный мяч имеет длину окружности l = 67 см, следовательно, радиус такого мячика составит 10,6 см. Зная радиус, вы без проблем можете определить, сколько синтетической кожи понадобится для создания одного изделия
Это означает, что для обшивки одного мяча вам понадобится 0,141 квадратных метров кожи.
Заключение
Объемные фигуры постоянно вращаются вокруг нас, поэтому задача определения площадей поверхностей и объемов многогранников остается актуальной задачей. Используйте наш каталог онлайн-калькуляторов и выполняйте необходимые расчеты для решения бытовых или производственных задач.