Как посчитать площадь неравностороннего многоугольника

Площадь неправильного четырехугольника

Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.

С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».

Как найти площадь неправильного четырехугольника?

Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.

Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

Источник

Площадь неравностороннего многоугольника

Использование различных формул площадей многоугольников

Т.к. площадь треугольника равна полупроизведению высоты и стороны, к которой эта высота проведена, то с одной стороны площадь равна \[S=\dfrac12\cdot 6\cdot 4,\] а с другой \[S=\dfrac12\cdot 8\cdot h,\] где \(h\) – высота, которую нужно найти.

Таким образом, получаем следующее равенство: \[\dfrac12\cdot 6\cdot 4=\dfrac12\cdot 8\cdot h \quad \Leftrightarrow \quad h=3.\] Ответ: 3 Задание 4 #2268 Уровень задания: Равен ЕГЭ В треугольнике \(ABC\): \(AC = 4\), \(AB = 6\), \(\cos <\angle BAC>= \dfrac<\sqrt<15>><4>\). Найдите площадь треугольника \(ABC\).

Из основного тригонометрического тождества:\(\sin^2\angle BAC = 1 — \dfrac<15><16>\), тогда \(\sin\angle BAC = \pm 0,25\).

Так как \(\angle BAC \in (0^<\circ>; 180^<\circ>)\), то \(\sin\angle BAC = 0,25\).

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними,тогда площадь треугольника \(ABC\) равна \(0,5\cdot 4 \cdot 6 \cdot 0,25 = 3\).

Как посчитать площадь многоугольника

Аналогичным образом измерьте и стороны самого многоугольника, натянув бечевку между соседними вершинами. 4 Чтобы воспользоваться формулой Герона, сначала посчитайте полупериметр каждого треугольника по формуле:р = ½ * (а + b + с),где:а, b и c – длины сторон треугольника,р – полупериметр (стандартное обозначение).Определив полупериметр треугольника, подставьте полученное число в следующую формулу:S∆ = √(р*(p-a)*(p-b)*(p-c)),где:S∆ – площадь треугольника. 5 Если многоугольник выпуклый, т.е.

не имеет внутренних углов, превышающих 180º, то выберите в качестве внутренней точки любую вершину многоугольника. В этом случае, треугольников получится на два меньше, что иногда может существенно упростить задачу нахождения площади многоугольника.

Правильный многоугольник.

Формула площади n-угольника через радиус описанной окружности: S = nR2 · sin360°2n Формула периметра правильного n-угольника:P = na Формула угла между сторонами правильного n-угольника: αn = n — 2 · 180°n Рис.3 1.

Формула площади правильного треугольника через радиус описанной окружности: S = R2 3√34 8. Угол между сторонами правильного треугольника: α = 60° Рис.4 Правильный четырехугольнику — квадрат.

Как узнать площадь многоугольника?

Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует.

Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.В первом случае он окажется треугольником, и можно воспользоваться одной из формул:

Фигура с четырьмя вершинами может оказаться параллелограммом:

Площади многоугольников

Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\).

Доказательство Пусть \(S\) – площадь треугольника \(ABC\). Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\). Докажем, что \[S = \dfrac<1><2>AB\cdot CH.\] Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\)

Площадь многоугольника

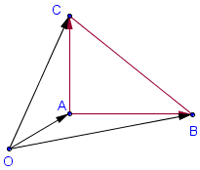
Ориентированная площадь треугольника – это обычная площадь, снабженная знаком.

Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами AB и AC. То есть ее знак зависит от порядка перечисления вершин.

1 треугольник АВС – прямоугольный.

Его ориентированная площадь равна S=|OB||OC|/2(она больше нуля, так как пара OB,OC ориентирована положительно).

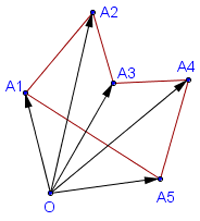
Точно так же для вычисления площади любого многоугольника A1A2.An нужно сложить ориентированные площади треугольников OA1A2,OA2A3. OAnA1

Рисунок №2 В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной A1A2.An многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Теперь необходимо выразить ее в координатах. Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.

Тогда его ориентированная площадь S будет равна: S=1/2(x1y2-y1x2+x2y3-y2x3+.+xny1-ynx1) Это и есть рабочая формула. Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S, вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади необхо­димо взять его абсолютное значение.

Формула для расчета площади неправильного многоугольника

Если да, то соседние.

В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин. Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым.

Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника. Как найти площадь правильного и неправильного шестиугольника?

Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см Подставим полученные результаты в нашу формулу: Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:

Площадь многоугольника

и — длины параллельных сторон, а — расстояние между ними (высота). и — длины диагоналей, и — угол между ними.

и — соответственно радиус и угол сектора (в ).

и — большая и малая полуоси эллипса.

Как вычислить площадь многоугольника

5 Используйте следующие формулы, когда известны стороны треугольника:– перемножьте стороны треугольника, которые прилежат к углу С, на синус этого угла;– вычтите из полупериметра (p) треугольника сначала одну сторону (p-a), потом другую (p-b) и третью (p-c). Перемножьте полученные значения с полупериметром и разделите результат на 2.

6 Применяйте для определения площади трапеции формулу S = h * ( a + b ) / 2, если известна высота и оба основания трапеции. 7 Используйте способ вычисления площади многоугольника с помощью палетки.

Начертите вокруг многоугольника квадратную сетку, у которой сторона одной клетки будет равна единице, чтобы все вершины многоугольника находились в ее узлах.

8 Вычислите площадь такой фигуры по формуле Пика: S = В + Г/2 – 1.

Источник

Площадь многоугольника

Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники

Пример многоугольника

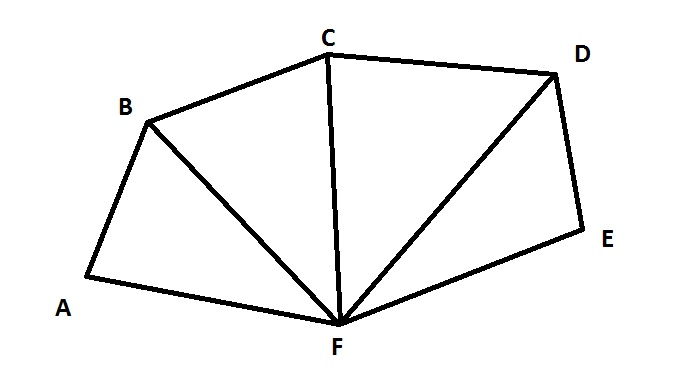
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.

Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.

А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.

Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).

По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».

Источник

Площадь правильного и неправильного пятиугольника: как рисовать, упражнения

Содержание:

В этом случае есть формула для вычисления точной площади правильного многоугольника, зная некоторые из его основных характеристик, которые мы выведем позже.

Если многоугольник не правильный, то есть имеет стороны разных размеров и неравные внутренние углы, единой формулы не существует.

Однако математики нашли методы вычислений, такие как разделение фигуры на другие с меньшим количеством сторон, такие как треугольники, квадраты и прямоугольники, размеры которых легко узнать или вычислить.

Как найти площадь правильного пятиугольника?

Мы собираемся взять правильный пятиугольник со стороной a и разделить его на 5 равных треугольников, как показано на рисунке, проведя отрезки от центра (красный) до вершин (синий).

В свою очередь, треугольники, как и тот, который выделен желтым справа на рисунке выше, делятся на два равных прямоугольных треугольника благодаря зеленому сегменту, который называется апофема.

Апофема определяется как перпендикулярный сегмент, который соединяет центр многоугольника с центром одной из сторон. Его длина L_К.

Площадь прямоугольного треугольника с основанием a / 2 и высотой L_К это:

Пентагон состоит из 10 таких треугольников, поэтому его площадь равна:

Но периметр п пятиугольника равно P =10а, поэтому площадь определяется как произведение периметра и длины апофемы:

Площадь правильного пятиугольника, знающая сторону a

Выражая длину апофемы L_К как функция стороны a, зная, что указанный угол составляет половину центрального угла, то есть 36º, что эквивалентно:

Методом элементарной тригонометрии через тангенс острого угла 36º:

загар (π / 5) = (a / 2) ÷ L_К

L_К= (а / 2) ÷ загар (π / 5)

Подставив в область, выведенную в предыдущем разделе, и зная, что P = 5a:

Площадь правильного пятиугольника, зная его радиус

cos 36º = cos (π / 5) = L_К ÷ R

sin 36º = sin (π / 5) = (a / 2) ÷ R

А = P x L_К / 2 = 5р. sin (π / 5) x R. cos (π / 5) = 5R 2 [sin (π / 5) x cos (π / 5)]

Используя формулу двойного угла:

грех (2θ) = 2 греха θ. cos θ

[sin (π / 5) x cos (π / 5)] = (1/2) sin 72º

Итак, подставив это значение, мы получим следующую формулу для площади правильного пятиугольника:

Как рассчитать площадь неправильного пятиугольника?

Триангуляция

Он состоит из деления фигуры на треугольники, площадь которых легче вычислить, или ее также можно проверить с другими фигурами, площадь которых известна, такими как квадраты, прямоугольники и трапеции.

Гауссовские детерминанты

Зная эти координаты, применяется гауссовский метод определителей для вычисления площади, которая определяется следующей формулой:

Полосы, сопровождающие формулу, представляют собой столбцы модуля или абсолютного значения.

Это означает, что даже если результат операции отрицательный, мы должны выразить его положительным знаком, а если он уже положительный, то его нужно оставить с этим знаком. Это потому, что площадь всегда является положительной величиной.

Процедура названа гауссовскими детерминантами в честь ее создателя, немецкого математика Карла Ф. Гаусса (1777-1855). Указанные операции эквивалентны определителю матрицы 2 × 2, например, первый определитель равен:

Чтобы найти площадь пятиугольника, мы должны решить 5 определителей, сложить результат алгебраически, разделить его на 2 и, наконец, выразить площадь всегда с положительным знаком.

Решенные упражнения

Упражнение 1

Решение

Поскольку это правильный пятиугольник, а у нас есть размеры стороны и апофемы, мы используем формулу, полученную выше:

Периметр P равен 5a = 5 x 5,9 см = 29,5 см.

A = 29,5 см x 4 см / 2 = 59 см 2

Упражнение 2.

Найдите площадь неправильного пятиугольника, как показано. Известны следующие размеры:

Решение

EA 2 + EC 2 = AB 2 + BC 2

Поскольку EA и AB измеряют одно и то же, отсюда следует, что:

Поскольку BC = 12, то ED = 12 / √2 = 8,485.

Используя эти значения, мы рассчитаем площадь каждого треугольника и добавим их в конце.

Площадь треугольника EDC

ED x DC / 2 = 8,485 2 / 2 = 36

Площадь треугольника AEC

EA x EC / 2 = EA x √2. ED / 2 = 5 x √2. 8 485/2 = 30

Площадь треугольника ABC

Тогда искомая область:

Это то же самое, что и треугольник AEC, поскольку они оба имеют одинаковые размеры.

Площадь неправильного пятиугольника

Наконец, запрашиваемая площадь представляет собой сумму площадей трех треугольников:

Источник

Площадь многоугольника по формуле Пика

Формула Пи́ка (или теорема Пи́ка) — классический результат комбинаторной геометрии и геометрии чисел, даёт выражение для площади многоугольника с целочисленными вершинами. Названа в честь Георга Пика, доказавшего её в 1899 году.

Площадь многоугольника в таком случае равна:

где S — площадь многоугольника, n — число узлов, лежащих строго внутри многоугольника, m — число узлов, лежащих на границах многоугольника, то есть либо на его сторонах, либо в вершинах.

В качестве примера вычислим площадь трапеции:

n = 25 (указаны синим цветом);

m = 24 (указаны оранжевым цветом).

Найдем площадь ниже представленного многоугольника:

n = 5 (указаны синим цветом);

m = 11 (указаны оранжевым цветом).

Онлайн калькулятор может быть использован для облегчения подсчетов при использовании теоремы Пика для вычисления площади многоугольника.

Формула Пика проста в понимании и удобна в применении. Во-первых, достаточно уметь считать, делить на 2, складывать и вычитать. Во-вторых, можно найти площадь и сложной фигуры, не затратив много времени. В-третьих, эта формула работает для любого многоугольника.

Недостаток в том, что Формула Пика применима только для фигур, которые нарисованы на клетчатой бумаге и вершины лежат на узлах клеток.

Онлайн калькуляторы

Актуальная информация

Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.

Источник