Как посчитать площадь неправильного треугольника
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
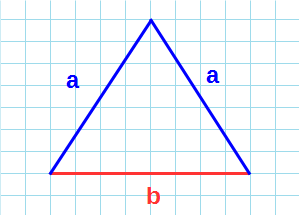
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
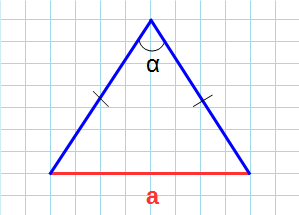
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
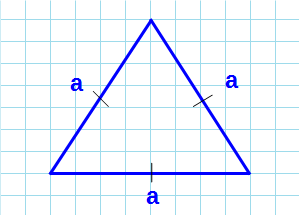
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Как найти площадь треугольника – все способы от самых простых до самых сложных
Зависит от того, какой треугольник.
Чтобы найти площадь треугольника, надо сначала определить тип треугольника: прямоугольный, равнобедренный, равносторонний. Если он у вас не такой – отталкивайтесь от других данных: высоты, вписанной или описанной окружности, длин сторон. Привожу все формулы ниже.
Если треугольник прямоугольный
То есть один из его углов равен 90 градусам.
Надо перемножить катеты и поделить на два. Катеты – это две меньшие стороны, в сравнении с гипотенузой. Гипотенуза – это самая длинная сторона, она всегда находится напротив угла в 90 градусов.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.
Если он равносторонний
То есть все три стороны равны. Ваши действия такие:
Если известна сторона и высота
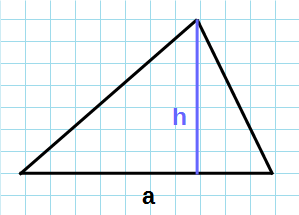
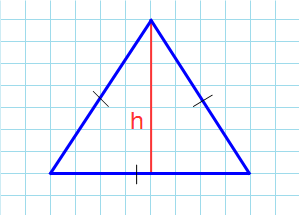
Площадь любого треугольника равна половине произведения стороны на высоту, которая к этой стороне проведена. Именно к этой, а не к какой-то другой.
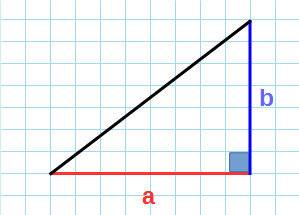
Чтобы провести высоту к стороне, надо найти вершину (угол), которая противоположна этой стороне, а потом опустить из нее на сторону прямую линию под углом в 90 градусов. На картинке высота обозначена синим цветом и буквой h, а линия, на которую она опускается, красным цветом и буквой a.
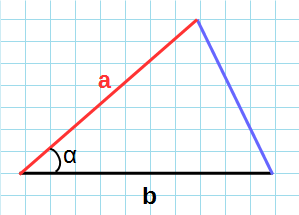
Если известны две стороны и градус угла между ними
Если вы знаете, чему равны две стороны и угол между ними, то надо найти синус этого угла, умножить его на первую сторону, умножить на вторую и еще умножить на ½:
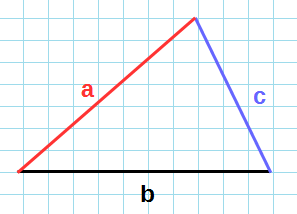
Если известны длины трех сторон
Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
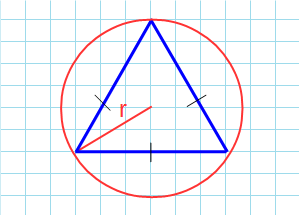
Если известны три стороны и радиус описанной окружности
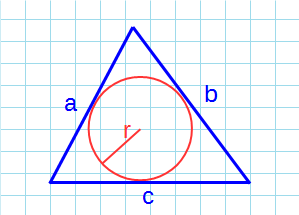
Окружность вы можете описать вокруг любого треугольника. Чтобы найти площадь «вписанного» треугольника – того, который «вписался» в окружность, надо перемножить три его стороны и поделить их на четыре радиуса. Смотрите картинку.
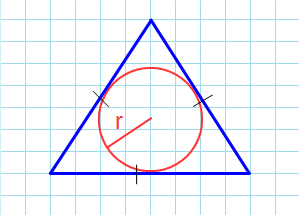
Если известны три стороны и радиус вписанной окружности
Если вам удалось вписать в треугольник окружность, значит она обязательно касается каждой из его сторон. Следовательно, расстояние от центра окружности до каждой из сторон треугольника – ее радиус.
Чтобы найти площадь, посчитайте сначала полупериметр – сложите все стороны и поделите на два. А потом умножьте его на радиус.
Это были все способы найти площадь треугольника. Спасибо, что дочитали статью до конца. Лайкните, если не трудно.
Калькулятор расчета площади треугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади треугольника по разным исходным данным: через основание и высоту, три стороны, две стороны и угол между ними, три стороны и радиус вписанной или описанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь треугольника.
1. Через основание и высоту
Формула расчета
2. Через длину трех сторон (формула Герона)
Примечание: если результат равен нулю, значит отрезки с указанными длинами не могут образовывать треугольник (следует из свойств треугольника).
Формула расчета:
p – полупериметр, который считается так:
3. Через две стороны и угол между ними
Примечание: максимальный угол в радианах не должен быть больше 3,141593 (приблизительное значение числа π ), в градусах – до 180° (исключительно).
Как найти площадь треугольника
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
3. Площадь треугольника через описанную окружность и стороны
4. Площадь треугольника через вписанную окружность и стороны
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
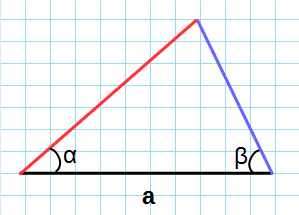
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
Площадь прямоугольного треугольника по формуле Герона
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Площадь треугольника онлайн
С помощю этого онлайн калькулятора можно найти площадь треугольника. Для нахождения площади треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
Площадь треугольника по основанию и высоте
Любой из сторон треугольника можно называть основанием треугольника. Если основание выбрана, то под словом «высота» понимают высоту треугольника, проведенную к основанию (Рис.1):
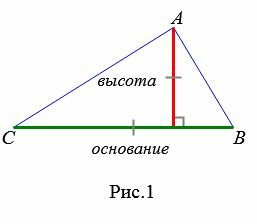 |
Теорема 1. Площадь треугольника равна половине произведения его основания на высоту.
Доказательство. Пусть AC основание треугольника ABC (Рис.2).
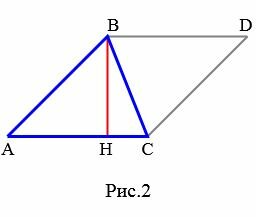 |
Проведем высоту BH. Обозначим через S площадь треугольника. Докажем, что
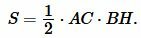  |
Следствие 1. Если высоты треугольников равны, то их площади относятся как основания.
Обозначим через k отношение
То есть отношение площадей треугольников с равными высотами равно отношению их оснований.
Следствие 2. Площадь прямоугольного треугольника равна половине произведения его катетов.
Действительно. Поскольку в прямоугольном треугольнике катеты перпендикулярны друг другу, то один из них можно определить как основание, а другой − как высоту. Тогда по теореме 1, площадь прямоугольного треугольника равна половине произведения его катетов.
Площадь треугольника по двум сторонам и углу между ними
Теорема 2. Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Доказательство. Обозначим через S площадь треугольника ABC и пусть a=BC, b=AC (Рис.3). Докажем, что
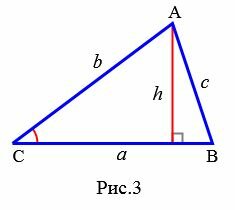 |
Площадь данного треугольника можно вычислить по формуле, полученной выше (теорема 1):
где h − высота треугольника.
Подставляя (2) в (1), получим:
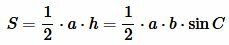 |
Площадь треугольника по стороне и прилежащим двум углам
Пусть известна сторона треугольника и две прилежащие углы (Рис.4).
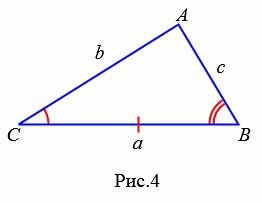 |
Найдем формулу площади этого треугольника. Обозначим через S площадь треугольника. Если у треугольника известны два угла, то можно найти и третий угол:
Найдем сторону b используя теорему синусов:
В предыдующем параграфе мы вывели площадь треугольника по двум сторонам и углу между ними. Подставляя (4) и (5) в (3), получим:
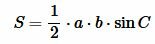 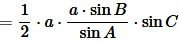 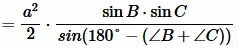 . . |
Площадь треугольника по трем сторонам. Формула Герона
Для нахождения площади треугольника по трем сторонам используют формулу Герона:
где a, b, c − стороны треугольника, а p − полупериод треугольника:
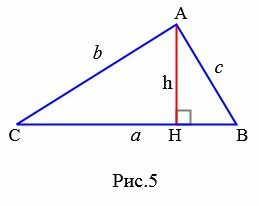 |
Доказательство формулы Герона. На рисунке 5 треугольник ABC имеет стороны a=BC, b=AC, c=AB. Проведем высоту h=AH. Обозначим x=CH. Тогда BH=a−x. Применим теорему Пифагора для треугольников AHC и AHB:
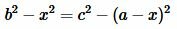 |
Подставляя (10) в (8) найдем h:
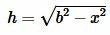 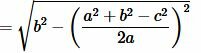 | (11) |
Тогда площадь треугольника равна:
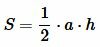 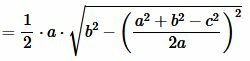 | (12) |
Преобразовав (12) получим формулу (7):
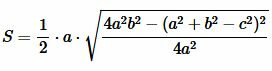 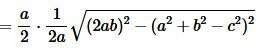 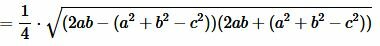 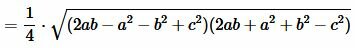 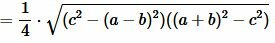 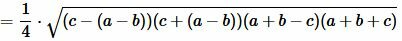 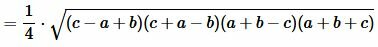 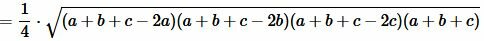 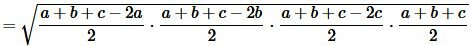 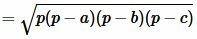 . . |
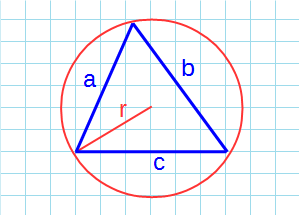
Площадь треугольника по трем сторонам и радусу описанной окружности
Пусть известны все три стороны треугольника и радиус описанной окружности (Рис.6). Докажем, что площадь треугольника равна: \( \small S=\frac<\large abc><\large 4R>. \)