Как посчитать площадь неправильного многоугольника
Площадь неправильного четырехугольника
Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.
С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».
Как найти площадь неправильного четырехугольника?
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.
где P — полупериметр, a, b, c, d — длины сторон четырехугольника.
Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.
где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.
В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.
Площадь многоугольника
Расчет площади многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники
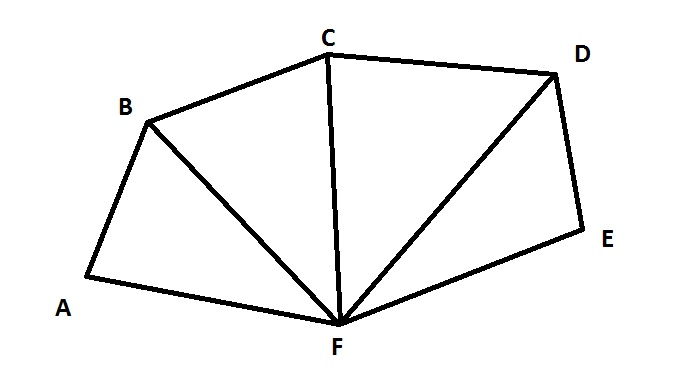
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».
Как узнать площадь многоугольника?
В задачах по геометрии часто требуется вычислить площадь многоугольника. Причем он может иметь довольно разнообразную форму – от всем знакомого треугольника до некоторого n-угольника с каким-то невообразимым числом вершин. К тому же эти многоугольники бывают выпуклыми или вогнутыми. В каждой конкретной ситуации полагается отталкиваться от внешнего вида фигуры. Так получится выбрать оптимальный путь решения задачи. Фигура может оказаться правильной, что существенно упростит решение задачи.
Немного теории о многоугольниках
Если провести три или более пересекающихся прямых, то они образуют некоторую фигуру. Именно она является многоугольником. По количеству точек пересечения становится ясно, сколько вершин у него будет. Они дают название получившейся фигуре. Это может быть:
Такая фигура непременно будет характеризоваться двумя положениями:
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют?
Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника. В выпуклом всегда все вершины лежат с одной стороны от такой прямой.
В школьном курсе геометрии большая часть времени уделяется именно выпуклым фигурам. Поэтому в задачах требуется узнать площадь выпуклого многоугольника. Тогда существует формула через радиус описанной окружности, которая позволяет найти искомую величину для любой фигуры. В других случаях однозначного решения не существует. Для треугольника формула одна, а для квадрата или трапеции совершенно другие. В ситуациях, когда фигура неправильная или вершин очень много, принято разделять их на простые и знакомые.
Как поступить, если фигура имеет три или четыре вершины?
В первом случае он окажется треугольником, и можно воспользоваться одной из формул:
Фигура с четырьмя вершинами может оказаться параллелограммом:
Формула для площади трапеции: S = н * (a + в) / 2, где а и в — длины оснований.
Как поступить с правильным многоугольником, у которого больше четырех вершин?
Для начала такая фигура характеризуется тем, что в ней все стороны равны. Плюс к этому, у многоугольника одинаковые углы.
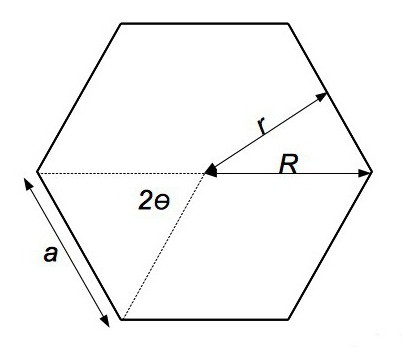
Если вокруг такой фигуры описать окружность, то ее радиус совпадет с отрезком от центра многоугольника до одной из вершин. Поэтому для того чтобы вычислить площадь правильного многоугольника с произвольным числом вершин, потребуется такая формула:
Sn = 1/2 * n * Rn 2 * sin (360º/n), где n — количество вершин многоугольника.
Из нее легко получить такую, которая пригодится для частных случаев:
Ситуация с неправильной фигурой
Выходом для того, как узнать площадь многоугольника, если он не является правильным и его нельзя отнести ни к одной из известных ранее фигур, является алгоритм:
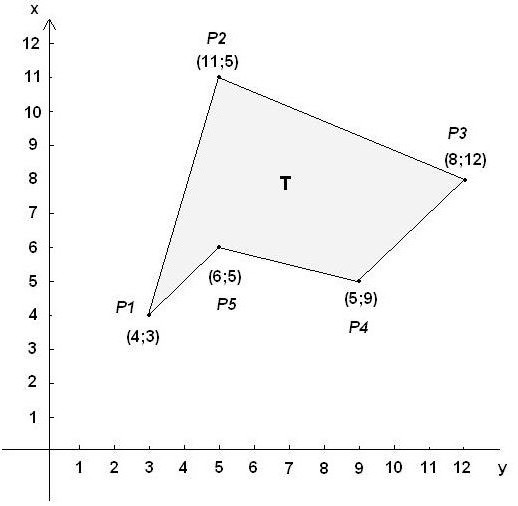
Что делать, если в задаче даны координаты вершин многоугольника?
Стоит отметить, что знак результата будет зависеть от обхода фигуры. При использовании указанной формулы и движении по часовой стрелке ответ будет получаться отрицательным.
Пример задачи
Условие. Координаты вершин заданы такими значениями (0.6; 2.1), (1.8; 3.6), (2.2; 2.3), (3.6; 2.4), (3.1; 0.5). Требуется вычислить площадь многоугольника.
Совет по решению задачи, для которой многоугольник изображен на бумаге в клетку
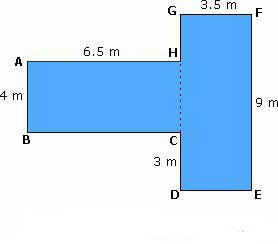
Чаще всего озадачивает то, что в данных имеется только размер клеточки. Но оказывается, что больше сведений не нужно. Рекомендацией к решению такой задачи является разбивание фигуры на множество треугольников и прямоугольников. Их площади довольно просто сосчитать по длинам сторон, которые потом легко сложить.
Но часто есть более простой подход. Он заключается в том, чтобы дорисовать фигуру до прямоугольника и вычислить значение его площади. Потом сосчитать площади тех элементов, которые оказались лишними. Вычесть их из общего значения. Этот вариант порой предполагает несколько меньшее число действий.
Расчет площади неправильного многоугольника онлайн
Здравствуйте, в этой статье мы постараемся ответить на вопрос: «Расчет площади неправильного многоугольника онлайн». Также Вы можете бесплатно проконсультироваться у юристов онлайн прямо на сайте.
Формула для расчета площади неправильного многоугольника
S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.
Площадь неправильного четырехугольника с заданными сторонами
Формула площади Гаусса (формула землемера или формула шнурования или алгоритм шнурования) — формула определения площади простого многоугольника, вершины которого заданы декартовыми координатами на плоскости.
Пользователь перемножает соответствующие координаты и складывает, чтобы найти область, охватывающую многоугольник, и вычитает его из окружающего многоугольника, чтобы найти площадь многоугольника внутри.
Это называется формулой шнурков, так как положительные и отрицательные слагаемые из перемножаемых координат располагаются на бумаге крест-накрест, как при завязке шнурков. Она находит применение в геодезии и лесном хозяйстве, среди других областей.
Формула была описана Мейстером (1724—1788) в 1769 году и Гауссом в 1795. Она может быть проверена путем деления многоугольника на треугольники, но её также можно рассматривать как частный случай теоремы Грина.
Калькулятор расчета площади земельного участка неправильной формы Полезные калькуляторы Конвертер единиц площади / Конвертер единиц длины Расчет площади прямоугольника a=ммсммкмфутярддюйммиля b=ммсммкмфутярддюйммиля Вычислить Расчет площади треугольника Способ нахождения площади треугольника: По трем сторонамПо одной стороне и высоте, опущенной на эту сторонуПо двум сторонам и углу между ними a=ммсммкмфутярддюйммиля b=ммсммкмфутярддюйммиля c= ммсммкмфутярддюйммиля град.рад. Вычислить Расчет площади параллелограмма Способ нахождения площади параллелограмма:По основанию и высоте параллелограммаПо двум сторонам и углу между нимиПо двум диагоналям и углу между ними a=ммсммкмфутярддюйммиля h=ммсммкмфутярддюйммиля c= ммсммкмфутярддюйммиля град.рад.
В разделе Дополнительное образование на вопрос Помогите, как найти площадь четырехугольника зная только его стороны( СТОРОНЫ ВСЕ РАЗНЫЕ ) нужно опереться на формулу ге заданный автором Опрос лучший ответ это Если известны только стороны, и больше НИЧЕГО, то площадь четырехугольника найти нельзя. Четырехугольник — нежесткая фигура. Для его задания четырех сторон недостаточно. Повторяю для ОСОБО ТУПЫХ: Этого сделать нельзя! А если разбить на треугольники, то надо знать длины третьих сторон этих треугольников! То бишь — ДИАГОНАЛИ! Формулы, употребляемой следующим отвечающим НЕ СУЩЕСТВУЕТ!
Есть формула
S^2=(p-a)*(p-b)*(p-c)*(p-d)-a*b*c*d*cos((A+C)/2)
. Где А и С — противоположные углы четырехугольника, a, b, с, d — стороны, р — полупериметр! Из этой формулы (если извлечь корень из обеих частей) получается формула БРАХМАГУПТЫ для площади четырехугольника! Но надо знать сумму противоположных УГЛОВ!
Ответ от 22 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Помогите, как найти площадь четырехугольника зная только его стороны( СТОРОНЫ ВСЕ РАЗНЫЕ ) нужно опереться на формулу ге
Ответ от Колосовые[новичек]
сначала найди р=0,5(а+б+с+д)
площадь=(р-а) (р-б) (р-с) (р-д) и все под корнем
р=9
площадь=60
Ответ 60
проверь ответ
Ответ от Ёемен Аркадьевич[гуру]
А ты упорный) ) Тебе уже отвечали что это сделать невозможно…. Только четырьмя сторонами четырехугольник не определен…
Ответ от Европейский[новичек]
найдем полупериметр: p=(a+b+c+d):2
1) p=(3+6+4+5):2=18:2=9
найдем площадь:
S=v(p-a)(p-b)(p-c)(p-d)
2) S=v(9-3)(9-6)(9-4)(9-5)=v6*3*5*4=v360=19
Ответ от Ёкилл[новичек]
!
Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны: Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см.
Для начала найдем полупериметр: используем найденное значение для расчета площади: Площадь четырехугольника, заданного координатами Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат.
В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Дан квадрат ABCD, расположенный в системе координат XY.
Пусть дан четырехугольник с двумя диагоналями d1=5 см;d2=4см. Острый угол между ними равен α = 30°. Формула площади четырехугольника через диагонали легко применяется для известных условий.
Подставим данные: На примере расчета площади четырехугольника через диагонали понимаем, что формула очень похожа на расчет площади параллелограмма.
Площадь четырехугольника по сторонам Когда известны длины сторон фигуры, можно применить формулу площади четырехугольника по сторонам. Для применения этих расчетов потребуется найти полупериметр фигуры.
Мы помним, что периметр – это сумма длин всех сторон. Полупериметр – это половина периметра. В нашем прямоугольнике со сторонами a, b, c, d формула полупериметра будет выглядеть так: Зная стороны, выводим формулу.
В произвольном четырехугольнике также можно использовать все элементы для вывода формулы площади четырехугольника. Для начала рассмотрим формулу площади четырехугольника через диагональ.
Для того, чтобы ее использовать потребуются длины диагоналей и размер острого угла между ними.
Зная необходимые данные можно проводить пример расчета площади четырехугольника по такой формуле: Половина произведения диагоналей и синуса острого угла между ними является площадью четырехугольника. Рассмотрим пример расчета площади четырехугольника через диагональ.
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
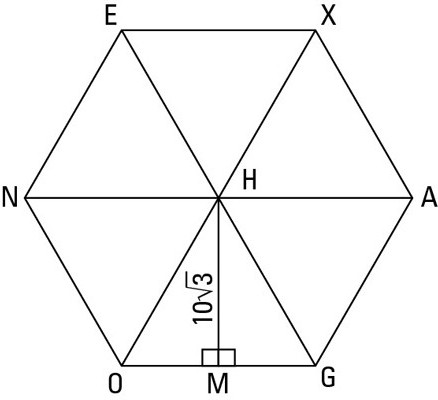
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.
Площадь неправильного шестиугольника по сторонам онлайн калькулятор
Получите бесплатную юредическую консультацию!
Калькулятор многоугольника Введите 3 величины Введите 2 величины Введите 3 величины для поиска объема Введите 1 величину Введите 1 величину
Многоугольник или полигон — геометрическая фигура, которая имеет n-ное количество углов.
Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны: Рассмотрим пример расчета площади четырехугольника через стороны. Дан произвольный четырехугольник со сторонами a = 5 см, b = 4 см, с = 3 см, d = 6 см.
Для начала найдем полупериметр: используем найденное значение для расчета площади: Площадь четырехугольника, заданного координатами Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат.
В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Дан квадрат ABCD, расположенный в системе координат XY.
Такой вариант подсчета площади пола более сложный, так как требует вычисления площади фигур, входящих в состав помещения по отдельности.
Для вычисления общей площади следует разбить пространство на несколько правильных фигур, в виде прямоугольников, трапеций, квадратов и т.д.
Например, если помещение имеет г-образную форму, то достаточно его разделить на два прямоугольника, вычислить площадь каждого из них и суммировать полученные результаты.
Площадь правильного многоугольника, формула
В итоге, покупка краски и определение количества отделочного материала для пола выполнится быстро. Не выполняйте замеры по стене, так как она может быть кривой и приведет к возникновению неточности в процессе определения площади пола.
Особой сложностью отличаются работы по определения площади пола, на котором имеются уступы в виде полукруга или волны. Данная ситуация предполагает измерение каждой из дуг, нахождение радиусов и раздробление площади на несколько геометрических фигур.
С помощью определения площади для каждой из них вычисляется общая формула асимметричного сегмента. Определение площади прямоугольной комнаты и потолка Прямоугольное помещение является наиболее типичным и часто встречающимся вариантом.
Для расчета площади достаточно длину помещения умножить на его ширину.
ВниманиеДля расчета площади пола в такой комнате требуется также разделить пространство на несколько частей, площадь которых вычисляется по отдельности. Бывают варианты помещений, которые имеют разные уровни пола, то есть возвышенности или уклоны.
Таким образом, помещение разделяется на несколько зон.
Например, в кухне выделяется столовая и рабочая части. То же самой и бывает с потолком, например, многоуровневым.
Для вычисления площади пола с уступами или возвышенностями, следует опять же разделить пространство на части в виде прямоугольников или квадратов, а те самые выступы, измерить линейкой и вычислить их площадь.
Таким способом получится провести расчет общей площади помещения.
Учтите, что в таком случае предпочтительно использовать рулетку, которая устанавливается вблизи основания. Кроме того, потребуется карандаш и тетрадь, для записывания всех значений.
ВажноПри планировке кухни в зданиях с жилой площадью более 55 квадратных метров, кухня должна занимать минимум пятую часть всего дома.
Если кухня занимает более 10 квадратных метров, возможен вариант ее использования в качестве столовой или комнаты для приема гостей. Минимальная ширина прихожей составляет 140 см, в ней также должно присутствовать естественное освещение.
Для детской комнаты достаточно площади в 10-15 метров квадратных. Самыми маленькими должны быть ванная и туалет. Их площадь ровняется 4-8 квадратным метрам.
Расчет площади Многоугольника, используя радиус вписанного круга и длину стороны:[ (A×P)/2 ][ Apothem(A) = side/(2×Tan(π/N)) ] Введите длину = Введите кол-во сторон = Площадь Многоугольника = Расчет площади по длине стороны:Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))Периметр Многоугольника = N * (side) Расчет площади по радиусу описанной окружности :Площадь Многоугольника = ½ * R² * Sin(2π / N) Расчет площади по радиусу вписанного круга :Площадь Многоугольника = A² * N * Tan(π / N)где, A = R * Cos(π / N) По радиусу вписанного круга и длине стороны :Площадь Многоугольника = (A * P) / 2где A = сторона / (2 * Tan(π / N))где,
Примеры: Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
После того, как мы определили нашу площадь, мы можем определить количество соток на земельном участке. Согласно общепринятым данным, в одной сотке – 100 м².
Далее при помощи простой арифметики, мы разделим наш параметр S на 100. Готовый результат и станет равен размеру делянки в сотках. Для нашего примера, этот результат – 8.
Таким образом, получаем, что площадь участка составляет восемь соток.
В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Наиболее полный и точный расчет можно произвести по координатам поворотных точек. Такие координаты определяются кадастровым инженером при проведении межевания участка.
Вычисление таких координат производится с помощью различных методов, указанных в приказе МЭР № 518 «О требованиях в точности определения характерных точек».
Данный онлайн калькулятор помогает произвести расчет, определение и вычисление площади земельного участка в онлайн режиме.
Представленная программа способна правильно подсказать, как выполнить расчет площади земельных участков неправильной формы.
Площадь четырехугольника представляет собой корень из произведения разности полупериметра с длиной каждой стороны: Рассмотрим пример расчета площади четырехугольника через стороны.
Для начала найдем полупериметр: используем найденное значение для расчета площади: Площадь четырехугольника, заданного координатами Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат.
Вы не любите рекламу? Мы ее тоже не любим, тем не менее доходы от рекламы предоставляют возможность функционирования нашего веб-сайта и бесплатного обслуживания наших посетителей.
Пожалуйста, подумайте, не стоит ли отменить блокировку рекламы на этом веб-сайте. Спасибо.
Такой вариант подсчета площади пола более сложный, так как требует вычисления площади фигур, входящих в состав помещения по отдельности.
Во многих случаях может потребоваться расчет площади земельного участка, например, в случае покупки, сдачи в аренду или проведении межевания.
Чтобы правильно выполнить расчет площади делянок, не нужно использовать сложные инструменты.
Мы берем деревянные колышки или металлические прутья и устанавливаем их в углах нашего участка. Далее при помощи измерительной рулетки определяем ширину и длину делянки. Как правило, достаточно выполнить замер одной ширины и одной длины, для прямоугольных или равносторонних участков.
Для примера, у нас получились следующие данные: ширина – 20 метров и длина – 40 метров.
Такая фигура непременно будет характеризоваться двумя положениями:
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.
Правильный многоугольник
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение.
Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.
2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены.
3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.
Формула площади четырехугольника по координатам используется для расчета площади фигур, которые располагаются в системе координат. В этом случае для начала требуется расчет длин необходимых сторон. В зависимости от типа четырехугольника может меняться и сама формула. Рассмотрим пример расчета площади четырехугольника, используя квадрат, который лежит в системе координат XY.
Шаг 1: Мы находим область.
Площадь = ((боковая длина) ² * N) / (4Tan (π / N))
= ((2) ² * 4) / (4 * Tan (3,14 / 4))
= (4 * 4) / 4 * Тан (0,785)
= 16/4 * 0,999
= 16 / 3,996
= 4.
Шаг 1: Мы находим область.
Площадь = ½ * R² * Sin (2π / N)
= (0,5) * 2 * * Sin (2 * 3,14 / 5)
= 0,5 * 4 * Сын (6,28 / 5)
= 2 * Грех (1.26)
= 2 * 0,95
Поверхность = 1,9.
Шаг 1: Мы находим радиус введенного круга.
A = R * Cos (π / N)
= 2 * Cos (3,14 / 5)
= 2 * Cos (0,63)
= 2 * 0,81
Апофеоз (радиус введенного круга) = 1,62.
Шаг 2: Мы находим область.
Площадь = A² * N * Tan (π / N)
= 1,62 × 5 5 Тан (3,14 / 5)
= 2,62 * 5 * Тан (0,63)
= 13,1 * 0,73
Поверхность = 9,5.
Задача 4.
Найдите область многоугольника с помощью Apofema (радиус введенного круга), если длина стороны равна 2, а количество страниц — 5.
Шаг 1: Мы находим Apophemus.
Apofem = длина страницы / (2 * Tan (π / N))
= 2 / (2 * Tan (π / 4))
= 2 / (2 * Tan (0,785))
= 2 / (2 * 0,999)
= 2 / 1,998
Апофеоз (A) = 1.
Площадь и периметр пятиугольника
Поэтому иногда вам нужно быть умным и использовать более сложные методы расчета.
Эти данные необходимы для планирования ремонта квартиры — вы можете рассчитать количество необходимых строительных материалов. Если работа, выполняемая наемными мастерами, часто требует оплаты за квадратный метр.
Чтобы не стать жертвой мошенничества, чтобы контролировать совесть сотрудника и не платить больше, объем выполненной работы должен быть надлежащим образом определен.
Нет необходимости использовать сложные инструменты, чтобы правильно рассчитать площадь участков.
Мы берем деревянные крюки или металлические стержни и размещаем их в углах нашего сайта.
Затем, используя измерительную ленту, измерьте ширину и длину графика.
Как правило, достаточно измерить одну ширину и одну длину для прямоугольных или односторонних секций.
Например, мы имеем следующие данные: ширина — 20 метров и длина — 40 метров.
Затем продолжите вычисление площади поверхности.
Прямоугольник — это простая двухмерная геометрическая фигура. Все углы у него прямые, по этому он и называется прямоугольник.
Стороны имеют разный размер, попарно, и обычно называются ширина и длина.
Умение рассчитывать площадь прямоугольника является базовым навыком для решения огромного количества бытовых или технических задач. Эти знания применяются практически во всех областях жизни! Например в тех случаях когда необходимы площади любых поверхностей в строительстве или недвижимости. При расчётах площадей земли, участков, стен домов, жилых помещений …
не возможно назвать ни одной области деятельности человека, где это знание не может пригодиться!
Если расчёт площади прямоугольника вызывает у Вас сложности — просто воспользуйтесь нашим калькулятором!
О моментально приведёт все необходимые вычисления и напишет текст решения с разъяснениями в деталях.
диагонали Прямоугольники соединяют противоположные точки изображения.
Чтобы успешно решить проблему нахождения диагонали прямоугольника, необходимо знать черты, которые у них есть:
Прямоугольник имеет диагонали одинаковой длины.
Давайте рассмотрим примеры решения проблем.
Пример.
Вокруг прямоугольника описывается окружность с радиусом 47 см.
где a — длина одной стороны.
Сторона пентагона и радиусы вписанной r и описанной окружности R приблизительно соотносятся как: Программный код калькулятора использует эти соотношения, что позволяет вам найти площадь правильного пятиугольника, зная только один параметр из перечисленных: радиус вписанной окружности; радиус описанной окружности; длина стороны.
Формула правильного многоугольника, зная стороны, представляет собой произведение количества сторон и квадрата длины, деленное на четыре тангенса угла, полученного делением 180 градусов на то же количество.
Угол правильного многоугольника зависит только от количества сторон и рассчитывается как 180 градусов, деленные на количество, и умноженные на разность количества сторон и двух. α=(n-2) (180°)/n
= (A * P) / 2 где A = / (2 * Tan(π / N))
Задача 1 : Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество = 4.
Как рассчитать площадь неправильного многоугольника с разными сторонами
Расчет площади Многоугольника, используя радиус вписанного круга и длину стороны:[ (A×P)/2 ][ Apothem(A) = side/(2×Tan(π/N)) ] Введите длину = Введите кол-во сторон = Площадь Многоугольника = Расчет площади по длине стороны:Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))Периметр Многоугольника = N * (side) Расчет площади по радиусу описанной окружности :Площадь Многоугольника = ½ * R² * Sin(2π / N) Расчет площади по радиусу вписанного круга :Площадь Многоугольника = A² * N * Tan(π / N)где, A = R * Cos(π / N) По радиусу вписанного круга и длине стороны :Площадь Многоугольника = (A * P) / 2где A = сторона / (2 * Tan(π / N))где,
Примеры: Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
Расчет площади по длине стороны: Площадь Многоугольника = ((side)² * N) / (4Tan(π / N)) Периметр Многоугольника = N * (side) Расчет площади по радиусу описанной окружности : Площадь Многоугольника = ½ * R² * Sin(2π / N) Расчет площади по радиусу вписанного круга : Площадь Многоугольника = A² * N * Tan(π / N) где, A = R * Cos(π / N) По радиусу вписанного круга и длине стороны : Площадь Многоугольника = (A * P) / 2 где A = сторона / (2 * Tan(π / N)) где,
Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
В целом такая геометрическая фигура может иметь абсолютно любой вид. К примеру, символы звезды и компаса, полигон для моделирования или грань шестеренки — многоугольники. Многоугольные фигуры разделяются на две группы:
Выпуклый полигон, у которого все углы равны и все стороны равны, считается правильным и имеет собственное название. К примеру, правильный пятиугольник называется пентагон, шести — гексагон, восьмиугольник — октагон, десятиугольник — декагон, одиннадцатиугольник — гендекагон, двенадцати — додекагон. Любой правильный многоугольник имеет свою вписанную и описанную окружность. При этом круг также можно представить как правильный полигон, который имеет бесконечное количество углов.
Невыпуклые многоугольники практически не распространены в реальной жизни: они довольно редко встречаются в природе, а в рукотворном виде она выступают в роли граней деталей машин. Многие морские организмы обладают пентасимметрией, и наиболее очевидным примером невыпуклой фигуры является морская звезда.
Правильные геометрические фигуры наоборот широко встречаются в природе. Наиболее очевидным примером являются пчелиные соты, каждая ячейка которых представляет собой гексагон. Такие гексагональные ячейки позволяют маленьким труженицам наиболее экономно использовать площадь улья, заполняя пространство без просветов. Кроме того, многие простейшие организмы, например радиолярии, имеют форму правильных полигонов.
Пчелиные соты — уникальный природный объект, который состоит из множества гексагональных призматических ячеек. Давайте подсчитаем, сколько таких шестиугольников находится в одних сотах. Для этого нам нужно узнать общую площадь и площадь одной ячейки. Из Википедии мы знаем, что стандартная рамка для сот имеет размеры 435 х 300 мм, соответственно, общая площадь составляет 130 500 квадратных миллиметров. Там же указано, что горизонтальный диаметр одной ячейки составляет примерно 5,5 мм. Горизонтальный диаметр полигона — это диаметр вписанной в него окружности, следовательно, мы знаем параметр r = 2,75 мм. Таким образом, при n = 6 площадь одной ячейки составляет:
Теперь мы можем узнать общее количество ячеек в одних сотах, которое выражается как 130500/26,19 = 4982
Снежинки имеют форму правильного треугольника или шестиугольника благодаря тому факту, что вода состоит из трех атомов и при переходе из одного агрегатного состояния в другое, молекулы воды соединяются с другими частицами и образуют треугольник или гексагон. Равносторонний треугольник — это такой же правильный полигон, как и другие, ведь он имеет три равных стороны и три равных угла. Соответственно, мы можем определить площадь такой снежинки, зная только длину стороны. Пусть сторона снежинки равна 8 условным единицам. Тогда для определения площади нам потребуется указать n = 3 и a = 8. Мы получим результат в виде:
Кроме площади абстрактной снежинки, наш калькулятор посчитал также радиусы вписанной и описанной окружности.
Пчелиные соты — уникальный природный объект, который состоит из множества гексагональных призматических ячеек. Давайте подсчитаем, сколько таких шестиугольников находится в одних сотах. Для этого нам нужно узнать общую площадь и площадь одной ячейки. Из Википедии мы знаем, что стандартная рамка для сот имеет размеры 435 х 300 мм, соответственно, общая площадь составляет 130 500 квадратных миллиметров. Там же указано, что горизонтальный диаметр одной ячейки составляет примерно 5,5 мм. Горизонтальный диаметр полигона — это диаметр вписанной в него окружности, следовательно, мы знаем параметр r = 2,75 мм. Таким образом, при n = 6 площадь одной ячейки составляет:
Теперь мы можем узнать общее количество ячеек в одних сотах, которое выражается как 130500/26,19 = 4982
Снежинки имеют форму правильного треугольника или шестиугольника благодаря тому факту, что вода состоит из трех атомов и при переходе из одного агрегатного состояния в другое, молекулы воды соединяются с другими частицами и образуют треугольник или гексагон. Равносторонний треугольник — это такой же правильный полигон, как и другие, ведь он имеет три равных стороны и три равных угла. Соответственно, мы можем определить площадь такой снежинки, зная только длину стороны. Пусть сторона снежинки равна 8 условным единицам. Тогда для определения площади нам потребуется указать n = 3 и a = 8. Мы получим результат в виде:
Кроме площади абстрактной снежинки, наш калькулятор посчитал также радиусы вписанной и описанной окружности.