Как посчитать площадь круга через диаметр
Площадь круга
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:
S=πr 2 – это произведение числа пи на квадрат радиуса.
Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметр 
или длину окружности 
.
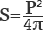
Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.
Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.
Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.
Результат работы калькулятора также округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.
Площадь круга
Существует несколько формул для нахождения площади круга. На нашем сайте мы предлагаем вам расчет по трем формулам. В зависимости от исходных данных, площадь круга можно найти через:
Круг — множество точек плоскости, удаленных от заданной точки этой плоскости (эту точку называют центр круга) на расстояние, не превышающее заданное (это расстояние — радиус круга).
Площадь круга онлайн калькулятор
Площадь круга через радиус
Чтобы найти площадь круга, зная его радиус, необходимо воспользоваться формулой:
S= \pi r^2
В этой формуле r — радиус круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через диаметр
Диаметр — отрезок, проходящий через центр окружности и соединяющий две точки на окружности. Диаметр равен двум радиусам.
Если известен диаметр круга, то его площадь можно найти по формуле:
S= \dfrac<\pi><4>d^2
Здесь d — диаметр круга, а \pi — число Пи, которое приблизительно равно 3,14.
Площадь круга через длину окружности
Длина окружности — это длина замкнутой плоской кривой, ограничивающей круг.
В случае, когда известна длина окружности, площадь круга можно рассчитать по следующей формуле:
S= \dfrac
Здесь l — длина окружности, а \pi — число Пи, которое приблизительно равно 3,14.
Онлайн калькулятор для расчета площади круга
Площадь круга можно найти, если известны:
Расчет площади круга — это не только учебная задача для школьников шестого класса. Круглых предметов довольно много и в реальной жизни, а необходимость посчитать их площадь хотя и не так часто, но возникает. Например, это может потребоваться для определения количества краски для ремонта круглой столешницы или для расчета площади остекления дома, спроектированного и построенного в готическом стиле.
Сложность вычисления площади круга связана с тем, что практически во всех формулах встречается иррациональное число пи, которое в обычных расчетах принимается равным 3,14. Даже если вы с детства неплохо владеете устным счетом, вычислить в уме площадь круга, радиус которого выражается дробным числом, будет довольно затруднительно. Но теперь это и не нужно, поскольку мы разработали для вас удобный сервис, который сделает все расчеты за несколько мгновений. Причем необязательно пересчитывать известные вам размеры конструкции так, чтобы получить значение радиуса в явном виде. Наш калькулятор умеет считать площадь круга практически по всем параметрам, которые могут быть известны на практике.
Расчет площади круга по его радиусу
Формула площади круга через диаметр
Если вам известен диаметр круга, можно разделить его пополам и подставить в предыдущую формулу. Но можно поступить еще проще. Перейдите на вторую вкладку и введите диаметр D в качестве исходных данных. Калькулятор использует формулу S = π · D2 / 4 и рассчитывает площадь круга прямо в процессе вашего ввода. Если после вывода результата вы измените значение диаметра, результат пересчитается автоматически.
Площадь круга через длину окружности
Для начала на всякий случай определимся с терминологией: окружность — это линия, каждая точка которой удалена на одинаковое расстояние от центра, а круг — это все, что находится внутри нее. Таким образом, окружность представляет собой внешнюю границу круга. Ее длина равна 2 · π · R (за R по-прежнему обозначаем радиус круга и окружности). Теоретически отсюда можно вычислить радиус и посчитать площадь круга по классической формуле. Но, опять же, есть более простой способ: воспользоваться нашим онлайн-калькулятором и ввести известную длину окружности, не выполняя ненужных промежуточных действий. Результат, как и всегда, будет выведен мгновенно.
Расчет площади круга по стороне вписанного квадрата
Как найти площадь круга, если известна сторона описанного вокруг него квадрата
Предположим, вы хотите купить бассейн, под который у вас выделен квадратный участок известных размеров. Вполне закономерно желание поставить резервуар максимальной емкости, которая определяется его высотой и площадью. То есть нужно найти площадь круга максимального радиуса, вписанного в квадрат, что и приводит к необходимости ее расчета через сторону этого квадрата. Нетрудно заметить, что задача сводится к вычислению площади круга по известному диаметру, так как сторона описанного вокруг него квадрата как раз и есть его диаметр. Но мы сделали для этого варианта отдельную вкладку, чтобы не заставлять вас запоминать ненужную информацию. Просто вводите длину стороны квадрата и получайте результат точно так же, как и во всех предыдущих случаях.
Вычисление площади круга через диагональ описанного квадрата
Расчет площади круга по площади описанного вокруг него квадрата
Условия использования онлайн-калькулятора расчета площади круга
Вы можете пользоваться данным сервисом совершено бесплатно. Количество расчетов не ограничено, калькулятор запускается из любого браузера, ничего устанавливать на ваш компьютер не нужно. Если наш сайт оказался полезным для вас, напишите об этом в комментариях и не забудьте сохранить его в закладках, чтобы иметь возможность выполнять любые математические вычисления, не отходя от компьютера.
Площадь круга
Площадь круга — это размер области внутри окружности, определенный в квадратных единицах измерения. Определять площадь круга можно по формулам, которые давно известны и использовались еще в Древнем мире для определения необходимого количества строительных материалов при построения зданий, амфитеатра и других архитектурных сооружений. В современном мире, с его быстрыми изменениями в архитектуре и в строительстве — определять площадь круга не менее важно. И в задачах алгебры и геометрии это умение пригодится.
Формулы площади круга
Площадь круга через радиус
В геометрии используются следующая формула для определения площади круга через радиус круга:
Здесь 
— площадь круга, 
— радиус круга.
В формуле фигурирует 
— это постоянная величина, которая называется «число » — это постоянная величина, которая часто используется в геометрии и в тригонометрии и означает отношение длины окружности к ее диаметру. Значение этого отношение получается постоянным, но не точным, и до сегодняшнего дня ученые стараются уточнить это значение. Приближенно «число » равно 3,14. Хотя после цифры «4» еще бесконечное количество цифр:
Площадь круга через диаметр
Давайте получим формулу площади круга через диаметр.
Так как диаметр — это два радиуса, то, следовательно, радиус — это половина диаметра:
— диаметр круга.
Подставим это выражение для радиуса в формулу площади круга, получим:
Таким образом, нами получена формула площади круга через диаметр круга:
Площадь круга через длину окружности
Окружность — это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: 
, тогда определим радиус и подставим его в формулу (1):
,
И формула площади круга через длину окружности:
Примеры решения задач
Задача 1
Найдите площадь круга, если известен его радиус 
см.
Решение: Для определения площади круга используем формулу (1):
Задача 2
Найдите площадь земельного участка, если известно, что форма участка — круг, а диаметр участка составляет 50 м.
Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):
Задача 3
Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.
Решение: граница участка круглой формы — это окружность. Тогда длина этой границы — это длина окружности. Площадь участка — площадь круга, которую мы определим по формуле (3) через длину окружности:
Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.
Площадь круга
Площадь круга — это размер области внутри окружности, определенный в квадратных единицах измерения. Определять площадь круга можно по формулам, которые давно известны и использовались еще в Древнем мире для определения необходимого количества строительных материалов при построения зданий, амфитеатра и других архитектурных сооружений. В современном мире, с его быстрыми изменениями в архитектуре и в строительстве — определять площадь круга не менее важно. И в задачах алгебры и геометрии это умение пригодится.
Формулы площади круга
Площадь круга через радиус
В геометрии используются следующая формула для определения площади круга через радиус круга:
Здесь — площадь круга, — радиус круга.
В формуле фигурирует — это постоянная величина, которая называется «число » — это постоянная величина, которая часто используется в геометрии и в тригонометрии и означает отношение длины окружности к ее диаметру. Значение этого отношение получается постоянным, но не точным, и до сегодняшнего дня ученые стараются уточнить это значение. Приближенно «число » равно 3,14. Хотя после цифры «4» еще бесконечное количество цифр:
Площадь круга через диаметр
Давайте получим формулу площади круга через диаметр.
Так как диаметр — это два радиуса, то, следовательно, радиус — это половина диаметра:
— диаметр круга.
Подставим это выражение для радиуса в формулу площади круга, получим:
Таким образом, нами получена формула площади круга через диаметр круга:
Площадь круга через длину окружности
Окружность — это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: , тогда определим радиус и подставим его в формулу (1):
,
И формула площади круга через длину окружности:
Примеры решения задач
Задача 1
Найдите площадь круга, если известен его радиус см.
Решение: Для определения площади круга используем формулу (1):
Задача 2
Найдите площадь земельного участка, если известно, что форма участка — круг, а диаметр участка составляет 50 м.
Решение: Чтобы найти площадь земельного участка, мы должны рассчитать площадь круга с диаметром 50 м. Используем формулу (2):
Задача 3
Длина границы земельного участка круглой формы равна 64 м. Найдите площадь участка.
Решение: граница участка круглой формы — это окружность. Тогда длина этой границы — это длина окружности. Площадь участка — площадь круга, которую мы определим по формуле (3) через длину окружности:
Для того, чтобы определять площадь круга в задачах по геометрии вам нужно определить с тем, какие данные вам известны и использовать те формулы для определения площади круга, которые больше всего подходят.