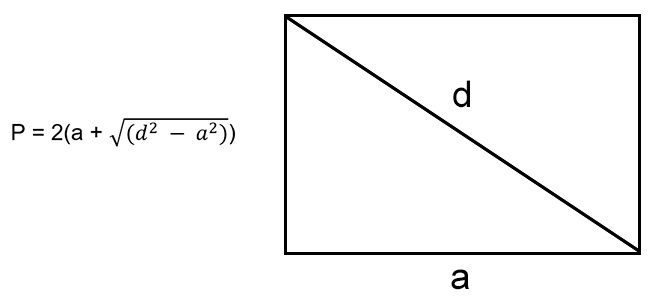Как посчитать периметр неправильного прямоугольника

Периметр

Периметр — это сумма длин всех сторон многоугольника.

Иногда для вычисления периметра геометрических фигур используются специальные формулы, в которых периметр обозначается заглавной латинской буквой « P ».

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

При нахождении периметра мы рекомендуем писать название фигуры маленькими буквами под знаком « P », чтобы не забывать чей периметр вы находите.

Периметр прямоугольника — это сумма длины и ширины, умноженная на « 2 ».

Стороны прямоугольника, которые лежат друг против друга (противолежащие), мы называем длиной и шириной.

AB = 3 см, BC = 7 см

P_ABCD = (AB + BC) · 2
P_ABCD = (7 + 3) · 2 = 10 · 2 = 20 (см)

Периметр квадрата — это длина стороны квадрата, умноженная на « 4 ».

KE = 7 см

P_EKFM = 4 · KE
P_EKFM = 4 · 7 = 28 (см)

Как найти периметр многоугольника

Периметр любого многоугольника (в том числе и периметр треугольника) рассчитывается по определению периметра. Для этого надо просто сложить длины всех сторон многоугольника.

P_ABCDE = AB + BC + CD + DE + EA = 3 + 4 + 3 + 2 + 2 = 14 (см)

Источник

Задачи на нахождение периметра и площади для 4 класса с ответами

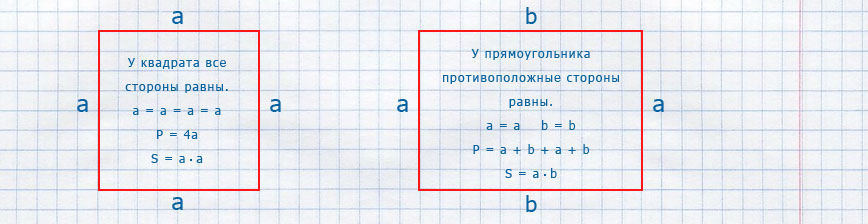
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:

Формулы площади и периметра для квадрата

P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата

Формулы площади и периметра для прямоугольника

P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника

Примеры решения задач разной сложности на нахождение периметра и площади

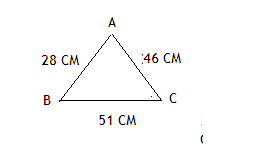
Задача 1

Каков периметр треугольника ABC?

Ответ: периметр треугольника равен 125 см.

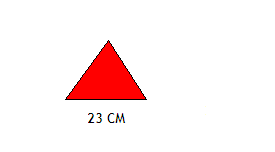
Задача 2

Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?

Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.

Задача 3

Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?

Задача 4

У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?

Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.

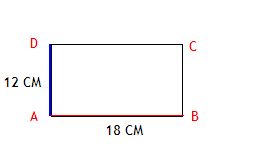
Задача 5

В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?

Ответ: Периметр прямоугольника равен 60 см.

Задача 6

Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?

Ответ: Площадь прямоугольника 56 м².

Задача 7

Площадь витрины квадратной формы 64м². Узнай ее периметр.

Ответ: Периметр витрины равен 32 м.

Задача 8

Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.

Ответ: Площадь прямоугольника равна 630 см².

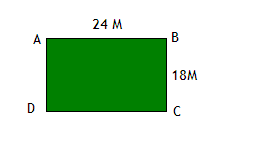
Задача 9

Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?

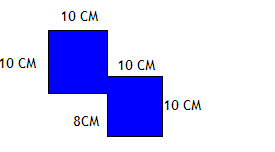
Задача 10

Каков периметр синей фигуры?

Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.

Ответ: Длина второго участка 40 м.

Задача 12

Найди периметр квадрата со стороной 8 см.

Ответ: Периметр квадрата 32 см.

Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.

Решение:

120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)

Ответ: Периметр бассейна 46 метров

Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.

Решение:

8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)

Ответ: Периметр прямоугольника 16 см.

Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?

Решение:

5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)

Ответ: Ученик ошибся на 3 см²

Ответ: Ширина другого участка 24 м.

У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?

Ответ: Площадь квадрата больше на 4 см.

Задача 20

Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.

У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.

Задача 22

Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?

1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36

Ответ: Незабудками засажено 36 м².

Задача 23

Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?

1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18

Ответ: Площадь прямоугольника 18 м².

Задача 24

Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?

1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см

Ответ: Периметр стола 280 см.

Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?

1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75

Ответ: Площадь прямоугольника 75 см².

Площадь квадрата 49 кВ дм. Узнайте его периметр.

1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)

Ответ: Периметр квадрата равен 28 дм.

Задача 27

Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.

1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32

Ответ: Площадь окна равна 32 м².

1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152

Ответ: Капустой засадили 1152 м².

Найди периметр квадрата со стороной 16 см.

Ответ: Периметр квадрата 64 см.

Задача 30

Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.

Ответ: Длина прямоугольника 13 см.

Задача 31

Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.

Ответ: Ширина прямоугольника 5 см.

Задача 32

Периметр квадрата 24 см. Найди его площадь.

24 : 4 = 6 (см)
6 · 6 = 36 (см²)

Ответ: Площадь квадрата 36 см².

Задача 33

Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.

Ответ: Площадь прямоугольника 56 см².

Задача 34

Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?

40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)

Ответ: Периметр прямоугольника 28 см.

Задача 35

Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.

Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.

У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).

Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)

Ответ: Площадь всех граней куба равна 24 см².

Задача 36

Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

Ответ: Площадь получившейся фигуры равна 44.

Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².

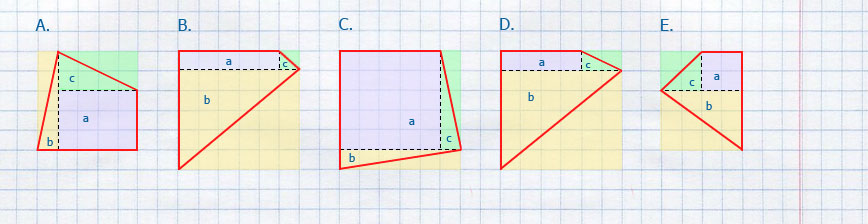
Задача 38

Найдите площади и периметры фигурок. Сделайте вывод.

Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²

Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.

Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.

Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.

Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.

Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.

Ответ: Периметр красной фигуры равен 27 см.

Задача 40

Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?

Ответ: Периметр равен 36 см.

Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?

Задача 42

Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.

Ответ: Периметр прямоугольника равен 24 см.

Задача 43

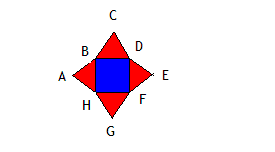
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?

Ответ: Расстояние пройденное улиткой будет равно 28 см.

Задача 44

В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?

Задача 45

Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?

Источник

Прямоугольник. Онлайн калькулятор

С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ прямоугольника, радиус описанной вокруг прямоугольника окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.

Определение 1. Прямоугольник − это параллелограмм, у которого все углы прямые (Рис.1).

Можно дать и другое определение прямоугольника.

Определение 2. Прямоугольник − это четырехугольник, у которого все углы прямые.

Свойства прямоугольника

Так как прямоугольник является параллелограммом, то все свойства параллелограмма верны и для прямоугольника.

Длиной прямоугольника называется более длинная пара его сторон.

Шириной прямоугольника называется более короткая пара его сторон.

Диагональ прямоугольника

Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.

На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.

Для вычисления длины диагонали воспользуемся теоремой Пифагора:

Из равенства (1) найдем d:

Пример 1. Стороны прямоугольника равны . Найти диагональ прямоугольника.

Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя в (2), получим:

Ответ:

Окружность, описанная около прямоугольника

Определение 4. Окружность называется описанной около прямоугольника, если все вершины прямоугольника находятся на этой окружности (Рис.3):

Формула радиуса окружности описанной около прямоугольника

Выведем формулу вычисления радиуса окружности, описанной около прямоугольника через стороны прямоугольника.

Нетрудно заметить, что радиус описанной около прямоугольника окружности равна половине диагонали (Рис.3). То есть

Подставляя (3) в (2), получим:

Пример 2. Стороны прямоугольника равны . Найти радиус окружности, описанной вокруг прямоугольника.

Решение. Для нахождения радиуса окружности описанной вокруг прямоугольника воспользуемся формулой (4). Подставляя в (4), получим:

Ответ:

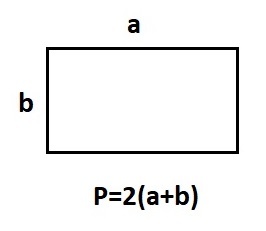
Периметр прямоугольника

Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.

Периметр прямоугольника вычисляется формулой:

где \( \small a \) и \( \small b \) − стороны прямоугольника.

Пример 3. Стороны прямоугольника равны . Найти периметр прямоугольника.

Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя в (5), получим:

Ответ:

Формулы сторон прямоугольника через его диагональ и периметр

Выведем формулу вычисления сторон прямоугольника, если известны диагональ \( \small d \) и периметр \( \small P \) прямоугольника. Заметим: чтобы прямоугольник существовал, должно удовлетворяться условие \( \small \frac P2>d \) (это следует из неравенства треугольника).

Чтобы найти стороны прямоугольника запишем формулу Пифагора и формулу периметра прямоугольника:

(6)

(7)

Из формулы (7) найдем \( \small b \) и подставим в (6):

(8)

(9)

Упростив (4), получим квадратное уравнение относительно неизвестной \( \small a \):

Вычислим дискриминант квадратного уравнения (10):

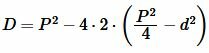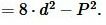(11)

Сторона прямоугольника вычисляется из следующих формул:

После вычисления \( \small a \), сторона \( \small b \) вычисляется или из формулы (12), или из (8).

Примечание. Легко можно доказать, что

Пример 4. Диагональ прямоугольника равна , а периметр равен . Найти стороны прямоугольника.

Решение. Для нахождения сторон прямоугольника воспользуемся формулами (11), (12) и (8). Найдем сначала дискриминант \( \small D \) из формулы (11). Для этого подставим , в (11):

Подставляя значения и в первую формулу (12), получим:

Найдем другую сторону \( \small b \) из формулы (8). Подставляя значения и в формулу, получим:

Ответ: ,

Признаки прямоугольника

Признак 1. Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

Признак 2. Если квадрат диагонали параллелограмма равен сумме квадратов его смежных сторон, то этот параллелограмм является прямоугольником.

Признак 3. Если углы параллелограмма равны, то этот параллелограмм является прямоугольником.

Источник

Как найти периметр прямоугольника

Периметр прямоугольника

Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.

Периметр прямоугольника — это сумма длин всех его ребер.

Основные свойства прямоугольника:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Варианты нахождения периметра прямоугольника

По сторонам

Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:

где \(a\) и \(b\) — это две соседние стороны фигуры.

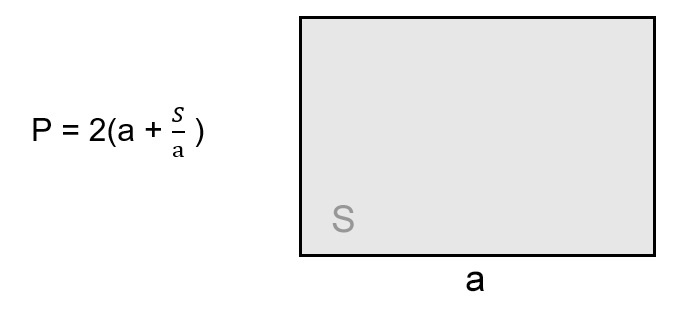
По любой стороне и площади

Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.

Получается, что формула для расчета \(P\) рассматриваемой фигуры будет выглядеть следующим образом:

По любой стороне и диагонали

В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.

где \(d\) — диагональ прямоугольника, а \(b\) — неизвестная сторона.

Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:

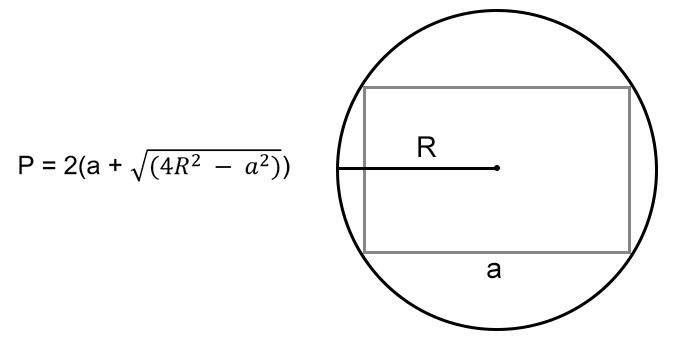
По любой стороне и радиусу описанной окружности

Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:

где \(R\) — радиус описанной окружности.

Тогда формула для расчета P будет выглядеть так:

Примеры решения задач

Задача 1

Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.

Решение:

Применяем самую первую формулу для расчета:

Задача 2

Решение:

Берем формулу \(P=2(\frac Sa+a)\) и подставляем известные значения:

Задача 3

Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.

Решение:

Вспоминаем формулу для расчета \(P=2(a+\sqrt)\) и вставляем известные величины:

Задача 4

Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.

Решение:

Источник