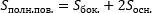Как посчитать объем треугольной призмы

Объем треугольной призмы: формула общего типа и формула для правильной призмы

В физике треугольная призма, сделанная из стекла, часто используется для изучения спектра белого света, поскольку она способна разлагать его на отдельные составляющие. В данной статье рассмотрим формулу объема прямой треугольной призмы.

Что такое треугольная призма?

Перед тем как приводить формулу объема треугольной призмы, рассмотрим свойства этой фигуры.

Помимо сторон, рассматриваемая призма характеризуется шестью вершинами (по три для каждого основания) и девятью ребрами (6 ребер лежат в плоскостях оснований и 3 ребра образованы пересечением боковых сторон). Если боковые ребра перпендикулярны основаниям, то такая призма называется прямоугольной.

Объем треугольной призмы общего типа

Как найти объем треугольной призмы? Формула в общем виде аналогична таковой для призмы любого вида. Она имеет такую математическую запись:

Величину So можно найти, если известны некоторые параметры для треугольника, например одна его сторона и два угла или две стороны и один угол. Площадь треугольника равна половине произведения его высоты на длину стороны, на которую опущена эта высота.

Что касается высоты h фигуры, то ее проще всего найти для прямоугольной призмы. В последнем случае h совпадает с длиной бокового ребра.

Объем правильной треугольной призмы

Общую формулу объема треугольной призмы, которая приведена в предыдущем разделе статьи, можно использовать для вычисления соответствующей величины для правильной треугольной призмы. Поскольку в ее основании лежит равносторонний треугольник, то его площадь равна:

Высота h является длиной ребра. Она никак не связана с основанием правильной призмы и может принимать произвольные значения. В итоге формула объема треугольной призмы правильного вида выглядит так:

Вычислив корень, можно переписать эту формулу так:

Таким образом, чтобы найти объем правильной призмы с треугольным основанием, необходимо возвести в квадрат сторону основания, умножить эту величину на высоту и полученное значение умножить на 0,433.

Источник

Геометрические фигуры

Объём призмы

Что такое треугольная призма?

Перед тем как приводить формулу объема треугольной призмы, рассмотрим свойства этой фигуры.

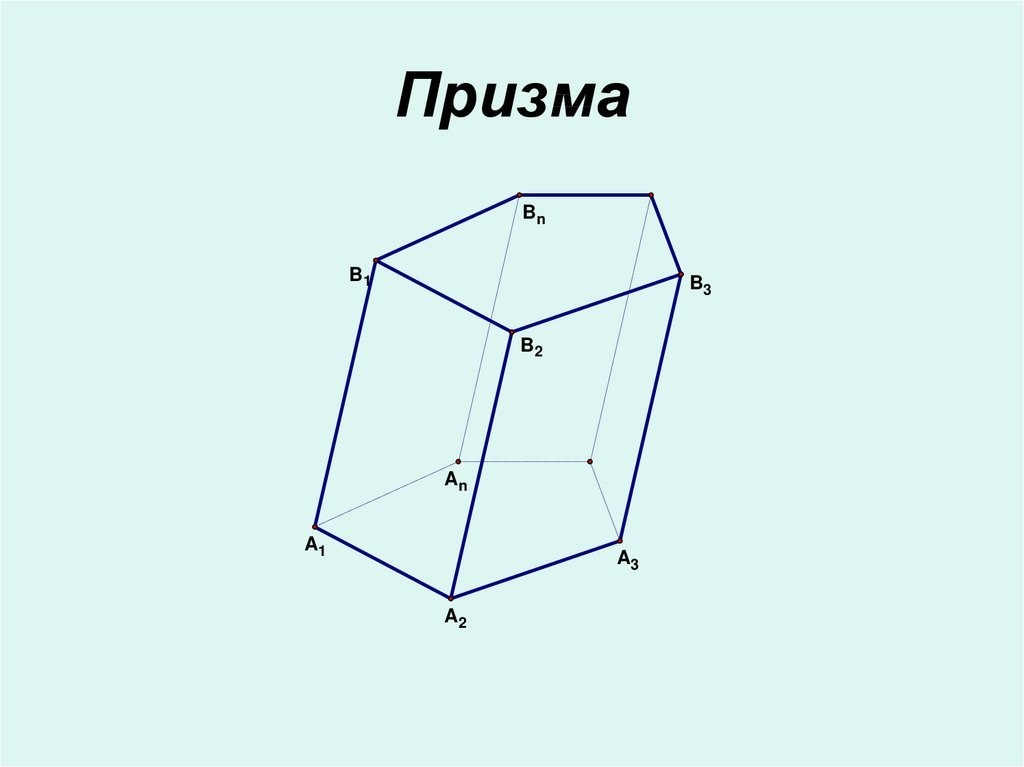
Чтобы получить этот вид призмы, необходимо взять треугольник произвольной формы и параллельно самому себе перенести его на некоторое расстояние. Вершины треугольника в начальном и конечном положении следует соединить прямыми отрезками. Полученная объемная фигура называется треугольной призмой. Она состоит из пяти сторон. Две из них называются основаниями: они параллельны и равны друг другу. Основаниями рассматриваемой призмы являются треугольники. Три оставшиеся стороны – это параллелограммы.

Помимо сторон, рассматриваемая призма характеризуется шестью вершинами (по три для каждого основания) и девятью ребрами (6 ребер лежат в плоскостях оснований и 3 ребра образованы пересечением боковых сторон). Если боковые ребра перпендикулярны основаниям, то такая призма называется прямоугольной.

Отличие треугольной призмы от всех остальных фигур этого класса заключается в том, что она всегда является выпуклой (четырех-, пяти-, …, n-угольные призмы могут также быть вогнутыми).

Правильная треугольная призма – это прямоугольная фигура, в основании которой лежит равносторонний треугольник.

Формула объема треугольной призмы правильной

Многогранник, который мы изучаем, будет правильным, если две его грани являются одинаковыми треугольниками равносторонними и три грани — это одинаковые прямоугольники. Формулу для объема такой призмы несложно получить из выражения общего вида, записанного в пункте выше. Чтобы это сделать, рассчитаем сначала площадь основания:

So = 1 / 2 × ha × a = 1 / 2 × √3 / 2 × a × a = √3 / 4 × a2

Значение высоты треугольника ha получено, исходя из того факта, что для равностороннего основания она является также медианой и биссектрисой. Таким образом, площадь So является функцией только одного параметра (стороны a).

Формулу объема для изучаемой призмы можно получить, если умножить на высоту выражение выше:

Поскольку для рассматриваемой фигуры высота равна длине бокового ребра b, то полученное выражение также можно переписать через параметры a и b.

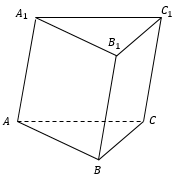
Элементы треугольной призмы

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Найти объем призмы, зная площадь основания и высоту

Найти объем правильной треугольной призмы, зная ребра

Объем правильной фигуры через значение ее диагонали

Треугольная призма является самой простой фигурой из своего класса, поэтому она обладает всего одним единственным типом диагонали. Это диагонали трех ее параллелограммов.

Предположим, что имеется правильная фигура, диагональ которой равна d (это диагональ прямоугольника), а высота равна h. Как рассчитать ее объем?

Для начала следует определить значение стороны основания a. Для этого воспользуемся теоремой Пифагора:

Тогда формула объема треугольной призмы приобретает вид:

V = √3 / 4 × a2 × h = √3 / 4 × (d2 — h2) × h

В случае правильной призмы объем всегда является функцией двух параметров (h и d в данном выражении).

Виды призм

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

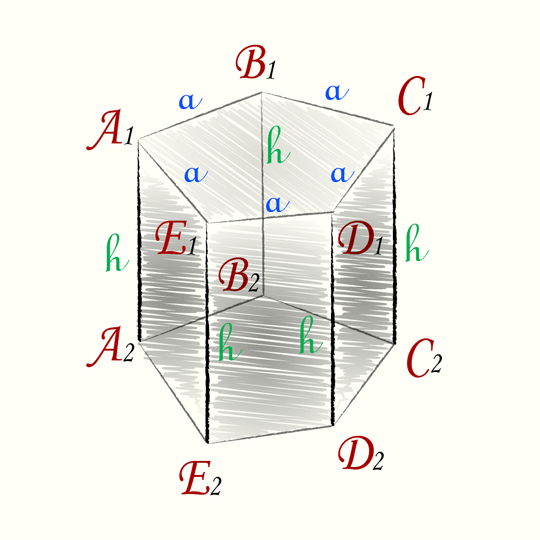
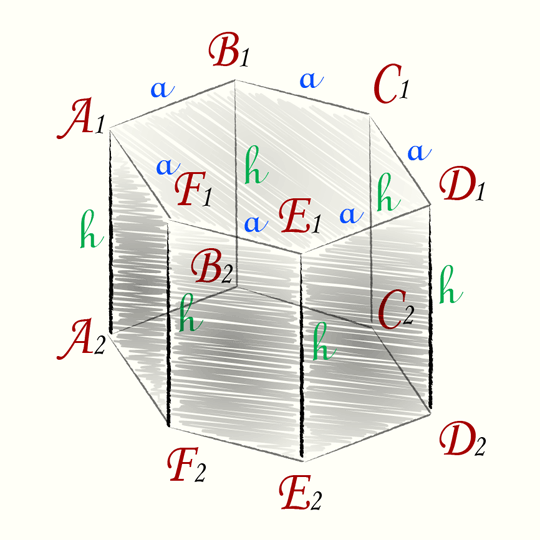
Вычисление объема правильной пятиугольной призмы

Формула вычисления объема призмы

Объем призмы равняется произведению площади ее основания на высоту.

V = S_осн ⋅ h

Приведенная выше формула подходит для следующих видов призм:

Необычная формула объёма призмы

– площадь сечения, перпендикулярного боковому ребру,

– длина бокового ребра.

Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.

Давай теперь для упражнения посчитаем объём самых популярных призм.

Как рассчитывать объем фигуры произвольного типа?

Часть пространства, которая ограничена плоскими сторонами геометрической фигуры, называется ее объемом. В общем случае для призмы абсолютно любого типа справедлива следующая формула для определения ее объема:

Как видно, она очень проста и содержит всего два множителя: So — площадь одного основания, h — высота призмы, то есть дистанция между ее основаниями.

Применительно к треугольной призме произвольной формы (наклонной и неправильной), для вычисления величины So можно воспользоваться универсальной формулой для треугольника:

Здесь a — сторона треугольника, ha — высота треугольника, опущенная на сторону a.

Расчет высоты h призмы можно провести с использованием теоремы Пифагора, если знать длину бокового ребра b и двугранные углы между основанием и боковыми гранями.

Вычисление объема трапецеидальной призмы

Основные свойства призмы

Объем треугольной призмы общего типа

Как найти объем треугольной призмы? Формула в общем виде аналогична таковой для призмы любого вида. Она имеет такую математическую запись:

Здесь h – это высота фигуры, то есть расстояние между ее основаниями, So – площадь треугольника.

Величину So можно найти, если известны некоторые параметры для треугольника, например одна его сторона и два угла или две стороны и один угол. Площадь треугольника равна половине произведения его высоты на длину стороны, на которую опущена эта высота.

Что касается высоты h фигуры, то ее проще всего найти для прямоугольной призмы. В последнем случае h совпадает с длиной бокового ребра.

Площадь поверхности призмы

Формула. Площадь поверхности правильной призмы через высоту ( h ), длину стороны ( a ) и количество сторон ( n ):

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

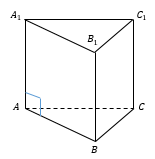
Объем прямой фигуры с прямоугольным треугольником в основании

Прямоугольный треугольник представляет собой фигуру из трех сторон, две из которых пересекаются под прямым углом. Эти стороны называются катетами. Обозначим их a1 и a2. Третья сторона называется гипотенузой (a3). Из планиметрии известно каждому школьнику, что если взять половину произведения катетов, то можно получить площадь рассматриваемого треугольника, то есть:

Так как призма является прямой, то достаточно умножить на So длину ее бокового ребра b, чтобы получить объем фигуры:

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

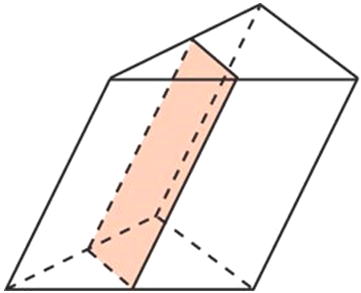
Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Источник

Треугольная призма все формулы и примеры задач

Треугольная призма — это трехмерное тело, образованное соединением прямоугольников и треугольников. В этом уроке вы узнаете, как найти размер внутри (объем) и снаружи (площадь поверхности) треугольной призмы.

Определение

Треугольная призма — это пятигранник, образованный двумя параллельными плоскостями, в которых расположены два треугольника, образующих две грани призмы, и оставшиеся три грани — параллелограммы, образованные со-сторонами треугольников.

Элементы треугольной призмы

Стороны граней являются ребрами призмы (A₁B₁, A₁C₁, C₁B₁, AA₁, CC₁, BB₁, AB, BC, AC), всего у треугольной призмы 9 граней.

Высотой призмы называется отрезок перпендикуляра, который соединяет две грани призмы (на рисунке это h).

Диагональю призмы называется отрезок, который имеет концы в двух вершинах призмы, не принадлежащих одной грани. У треугольной призмы такой диагонали провести нельзя.

Площадь основания — это площадь треугольной грани призмы.

Площадь боковой поверхности призмы — это сумма площадей четырехугольных граней призмы.

Виды треугольных призм

Треугольная призма бывает двух видов: прямая и наклонная.

У прямой призмы боковые грани прямоугольники, а у наклонной боковые грани — параллелограммы (см. рис.)

Прямая треугольная призма

Призма, боковые ребра которой перпендикулярны плоскостям оснований, называется прямой.

Наклонная треугольная призма

Призма, боковые ребра которой являются наклонными к плоскостям оснований, называется наклонной.

Основные формулы для расчета треугольной призмы

Объем треугольной призмы

Чтобы найти объем треугольной призмы, надо площадь ее основания умножить на высоту призмы.

Объем призмы = площадь основания х высота

Площадь боковой поверхности призмы

Чтобы найти площадь боковой поверхности треугольной призмы, надо периметр ее основания умножить на высоту.

Площадь боковой поверхности треугольной призмы = периметр основания х высота

Площадь полной поверхности призмы

Чтобы найти площадь полной поверхности призмы, надо сложить ее площади оснований и площадь боковой поверхности.

Правильная призма — прямая призма, основанием которой является правильный многоугольник.

Свойства призмы :

Верхнее и нижнее основания призмы – это равные многоугольники.
Боковые грани призмы имеют вид параллелограмма.
Боковые ребра призмы параллельные и равны.

Пример призмы

В этом примере:
— ABC и DEF составляют треугольные основания призмы
— ABED, BCFE и ACFD являются прямоугольными боковыми гранями
— Боковые края DA, EB и FC соответствуют высоте призмы.
— Точки A, B, C, D, E, F являются вершинами призмы.

Задачи на расчет треугольной призмы

Задача 1. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
Решение: Объем прямой призмы равен V = Sh, где S — площадь основания, а h — боковое ребро. Площадь основания в данном случае это площадь прямоугольного треугольника (его площадь равна половине площади прямоугольника со сторонами 6 и 8). Таким образом, объём равен:

V = 1/2 · 6 · 8 · 5 = 120.

Задача 2.

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Решение:

Объём призмы равен произведению площади основания на высоту: V = S_осн ·h.

Треугольник, лежащий в основании исходной призмы подобен треугольнику, лежащему в основании отсечённой призмы. Коэффициент подобия равен 2, так как сечение проведено через среднюю линию (линейные размеры большего треугольника в два раза больше линейных размеров меньшего). Известно, что площади подобных фигур соотносятся как квадрат коэффициента подобия, то есть S₂ = S₁k 2 = S₁2 2 = 4S₁.

Площадь основания всей призмы больше площади основания отсечённой призмы в 4 раза. Высоты обеих призм одинаковы, поэтому объем всей призмы в 4 раза больше объема отсечённой призмы.

Источник

Объем призмы

Вы будете перенаправлены на Автор24

На этой странице вы узнаете, что такое призма и как найти объем правильной треугольной или любой другой призмы. Также приведены формулы и онлайн-калькуляторы для расчёта объёма правильной треугольной призмы и призмы в общем случае.

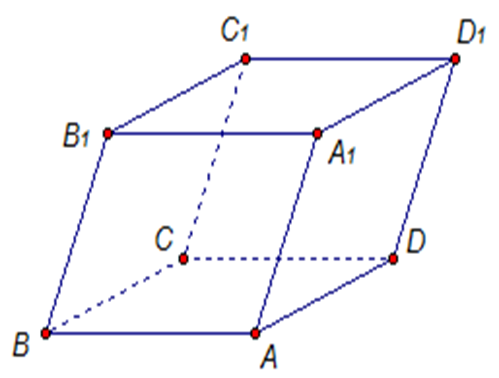
Призма — это объёмная фигура, 2 грани которой являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани представляют собой параллелограммы. Грани, лежащие в параллельных плоскостях, называются основаниями, а параллелограммы, имеющие общие стороны с основаниями, называются боковыми гранями.

Объем призмы через площадь основания и высоту

В общем случае объём любой призмы вне зависимости от того, правильная она или нет, определяется по формуле:

$S$ — площадь многоугольника, лежащего в основании;

Для того чтобы воспользоваться онлайн-калькулятором для вычисления площади призмы с произвольным многоугольником в основании, введите значение площади основания и высоту призмы.

Задача

Решение:

Для того чтобы найти объём призмы, сначала необходимо найти площадь её основания. Для этого воспользуемся формулой для вычисления площади правильного многогранника:

Теперь найдём объём призмы:

$V = S \cdot h = 42,81 \cdot 7 = 299,67$ куб. см.

Введём заданные значения в поля ввода калькулятора. Результаты совпадают, а значит, ответ найден верно.

Один из наиболее часто встречающихся видов призм — это полуправильная треугольная. В основании такой призмы лежит правильный треугольник (то есть, треугольник, у которого все стороны равны), а боковыми гранями являются прямоугольники.

Расчёт объёма полуправильной треугольной призмы можно осуществить с помощью онлайн-калькулятора. Для этого введите длину ребра и сторону основания в соответствующие поля ввода.

Объем правильной треугольной призмы через ребро

Чтобы вычислить объём правильной треугольной призмы, необходимо воспользоваться формулой объёма для призмы в общем случае:

затем подставим в эту формулу значение площади для правильного треугольника и получим:

$V =\frac<\sqrt3> <4>\cdot b^2 \cdot h$, здесь

$b$ — сторона правильного треугольника, лежащего в основании.

Задача

Решение:

Воспользуемся формулой для определения объема треугольной призмы:

Сверим полученный результат с калькулятором — ответы совпадают, значит, решение найдено верно.

Источник

Объем призмы

Что такое призма

Призма — это трехмерное геометрическое тело с двумя равными основаниями и плоскими гранями. Название зависит от фигуры, которая лежит в ее основании. Например, если это треугольник, призму называют «треугольной».

Эта объемная фигура может быть нескольких видов:

Формулы вычисления объема правильной призмы

Правильные призмы могут быть разных видов, в зависимости от многоугольника, который лежит в их основании. Формула вычисления объема во всех случаях выглядит одинаково:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Разница лишь в том, каким образом находится площадь S для каждой из фигур.

Треугольная

Чтобы вычислить объем призмы, в основании которой лежит правильный треугольник, используем формулу:

Где \(\frac<\sqrt3>4\cdot a^2=S\) — площадь правильного треугольника в основании, a — сторона треугольника, h — высота всей фигуры.

Четырехугольная

Для фигуры, в основании которой лежит квадрат, используем следующую формулу для вычисления объема:

Где a — сторона квадрата.

Пятиугольная

В этом случае объем будет вычисляться по формуле:

Шестиугольная

Для призмы с правильным шестиугольником в основании формула объема выглядит так:

Объем наклонной и прямой

Он находится через произведение площади основания на высоту:

Таким образом, формула вычисления объема совпадает с предыдущими вариантами и зависит лишь от фигуры в основании.

С прямой призмой все то же самое. Сначала нужно вычислить площадь ее основания, а потом умножить на высоту.

Примеры задач

Так как уже дана площадь основания, нам не важно какая фигура лежит в основании. Подставляем известные значения в формулу:

\(V=S\cdot h=12\cdot5=60 \) \(см^3\)

В основании прямой призмы лежит четырехугольник со сторонами a и b по 6 см и 3 см. Высота данной фигуры равна 10 см. Рассчитать ее объем.

Так как сначала для вычисления объема нам нужно определить площадь четырехугольника, будем использовать уравнение: \(V=a\cdot b\cdot h\)

Подставляем значения: \(V=6\cdot3\cdot10=180\) \(см^3\)

Источник