Как посчитать объем неравностороннего параллелепипеда

Объем параллелепипеда

Понятие объема

Чтобы без труда вычислить объём любой фигуры, нужно разобраться с определениями.

Объём — это количественная характеристика пространства, занимаемого телом или веществом.

Другими словами, это то, сколько места занимает предмет.

Объём измеряется в единицах измерения размера пространства, занимаемого телом, то есть в кубических метрах, кубических сантиметрах, кубических миллиметрах.

За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (см 3 ), кубический миллиметр (1 мм 3 ), кубический метр (1 м 3 ).

Объём всегда выражается в положительных числах. Это число показывает, какое именно количество единиц измерения есть в теле. Например, сколько воды в бассейне, сока в графине, земли в клумбе.

Два свойства объёма

Любое объемное тело имеет объем. Получается, при желании мы можем вычислить объем кружки, смартфона, вазы, кота — чего угодно.

Объем прямоугольного параллелепипеда

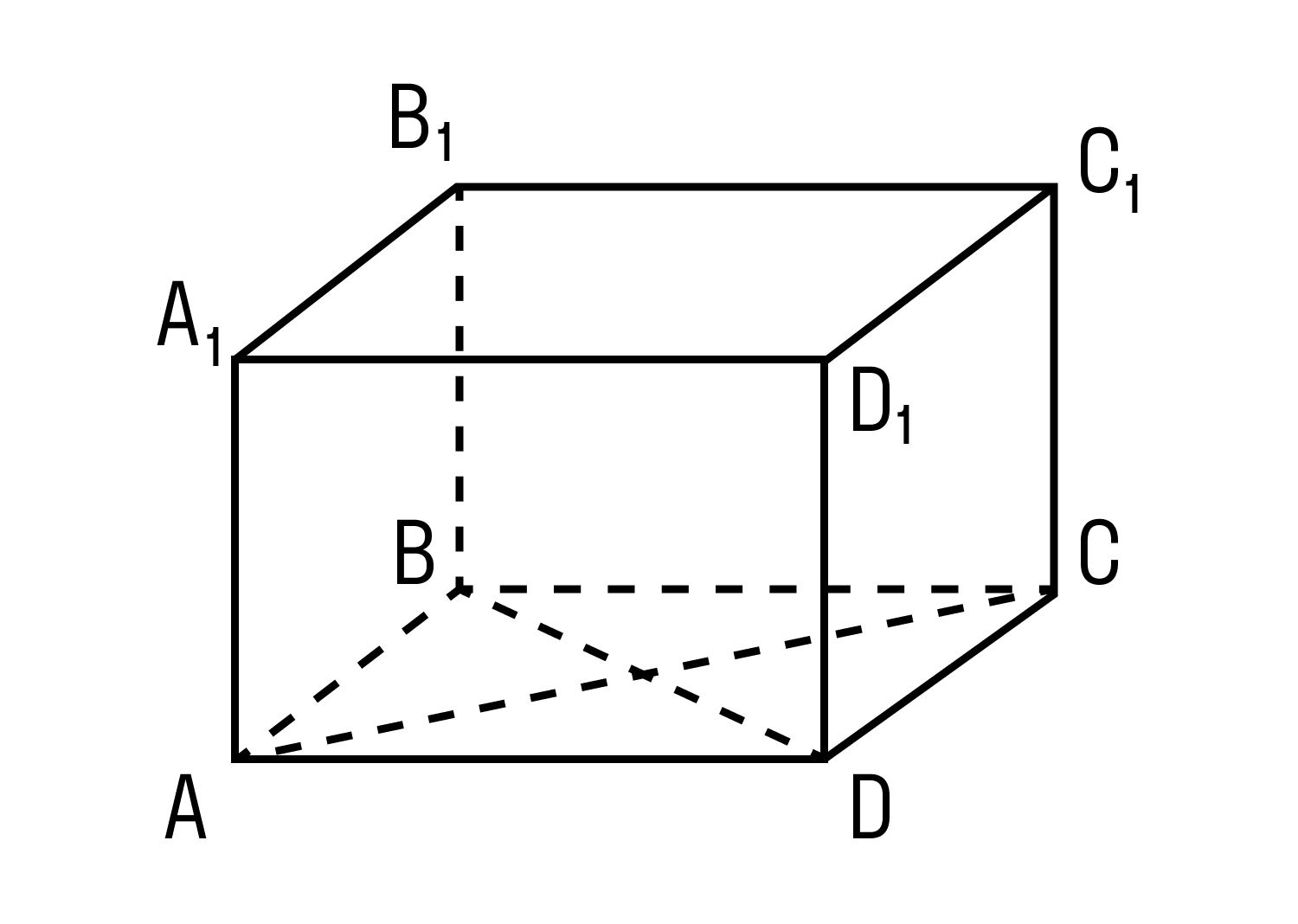
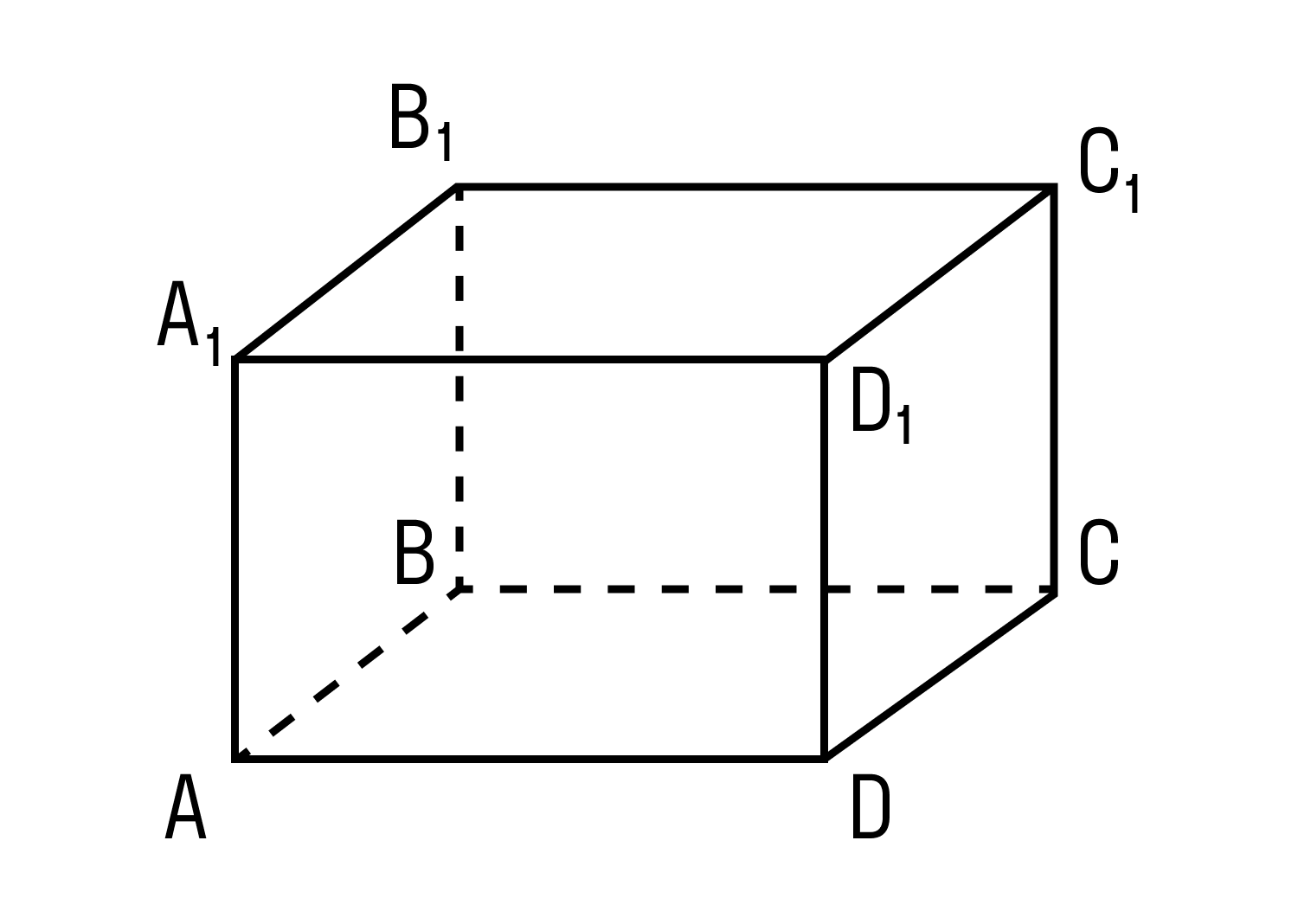
Параллелепипед — это многогранник с шестью гранями, каждая из которых является параллелограммом.

Прямоугольным параллелепипедом называют параллелепипед, у которого все грани являются прямоугольниками.

Формула объема прямоугольного параллелепипеда

Чтобы вычислить объем прямоугольного параллелепипеда, найдите произведение его длины, ширины и высоты:

V = a × b × h

Чтобы не запутаться в формулах, запоминайте табличку с условными обозначениями.

Источник

Объемы фигур. Объем параллелепипеда.

Объем прямоугольного параллелепипеда, формула.

Параллелепипедом является призма, основание у которой – это параллелограмм. У параллелепипеда

6 граней, а они, в свою очередь, являются параллелограммами.

Прямой параллелепипед, у которого все 6 граней прямоугольники, является прямоугольным.

Другими словами, прямоугольный параллелепипед — это объемная фигура, у которой есть 6 граней, и

Объем прямоугольного параллелепипеда равен произведению площади основания на высоту:

a – длина параллелепипеда,

b – ширина параллелепипеда,

Примеры прямоугольного параллелепипеда: спортивный зал, кирпич, картонная коробка или столешница

Длины 3 рёбер прямоугольного параллелепипеда, которые имеют общий конец, называются измерениями

прямоугольного параллелепипеда.

Прямоугольный параллелепипед с одинаковыми измерениями является кубом. Все 6 граней куба — это

Квадрат длины диагонали прямоугольного параллелепипеда = сумме квадратов 3 его измерений.

Объем прямого параллелепипеда, формула.

Как найти объем параллелепипеда?

Площадь боковой поверхности параллелепипеда, формула:

где Р_о — периметр основания,

Площадь полной поверхности, формула

где S_о — площадь основания

Формула объёма прямого параллелепипеда:

Объем произвольного параллелепипеда.

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры.

Чему равен объём параллелепипеда? Объем параллелепипеда равен абсолютной величине смешанного

произведения трёх векторов, которые определяются 3-мя сторонами параллелепипеда, которые исходят

Соотношение длина сторон параллелепипеда – угол между ними даёт утверждение, что определитель

Грама указанных 3х векторов равен квадрату их смешанного произведения.

Источник