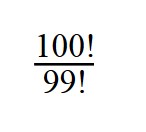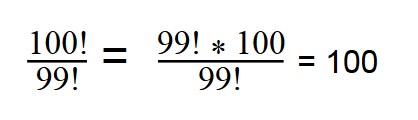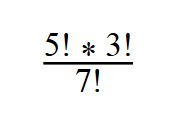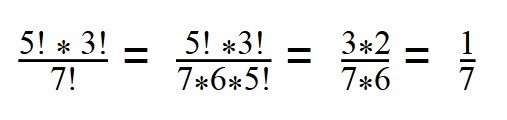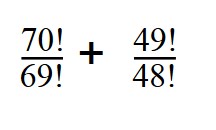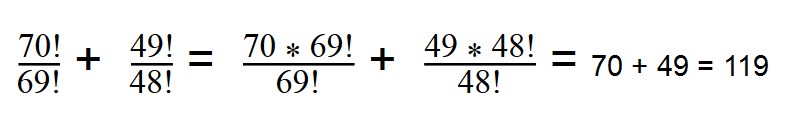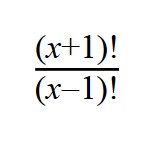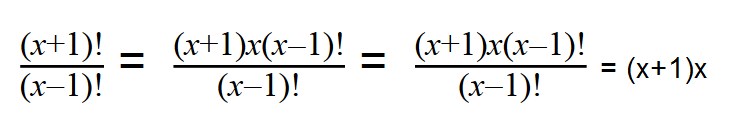Как посчитать нули в факториале
Подсчет конечных нулей факториала числа в любой системе счисления
Как я могу посчитать количество конечных нулей факториала числа в определенной системе счисления?
Давайте рассмотрим случай, когда мы находимся в 10-й системе счисления, а затем посмотрим, как мы можем обобщить это в универсальное решение. Нам дано число N и для его факториала нужно найти количество конечных нулей. Решение будет довольно простым — сумма:
Её мы можем обобщить в такую формулу:
Почему 5? Это просто. Конечный ноль получается только тогда, когда в составе факториала число имеет 10. Таким образом, посчитав количество десяток в факториале, мы узнаем количество конечных нулей.
Почему в примере выше мы делим на 5? Потому что 10 может быть получено умножением 5 на 2. Поэтому полное решение будет иметь две формулы:
Но, рассуждая логически, мы знаем, что первая сумма будет меньше, поэтому нам нужно посчитать только её (подробнее можно почитать тут).
Решение нашей проблемы
Для подсчёта конечных нулей факториала числа в определенной системе счисления я составил алгоритм, приведенный ниже:
Но двойка встречалась дважды при разложении 12-и, поэтому конечный результат мы делим на 2 и округляем до меньшего целого. В результате получаем 1.
Проделываем тоже самое с 3:
Таким образом, мы получили два частных от делений числа N на простые множители числа системы счисления. Они оба равны 1, поэтому меньшее нам выбирать не приходится и мы просто даем ответ — 1.
Рассмотрим еще один пример.
Пусть число N = 16, система счисления B = 16. Факториал 16! = 20922789888000, а 20922789888000 в 16-ой системе — 130777758000. Мы видим, что в конечной системе счисления факториал исходного числа имеет три ноля. При разложении 16 на простые множители, получим 2, 2, 2, 2. Здесь у нас только одно уникальное число, поэтому пункт 2 выполняется только один раз:
При разложении у нас было четыре двойки, поэтому сумму делений делим на 4 с округлением до меньшего целого:
Анализ алгоритма
Факториал числа n равен произведению чисел от 1 до n. Ноль в конце произведения появляется в результате перемножения 2 и 5. Но поскольку при разложении на простые множители числа n! двоек больше чем пятерок, то количество нулей в конце n! равно количеству пятерок в разложении n! на простые множители. Это число равно



Суммирование происходит до тех пор, пока очередное слагаемое не станет равным 0.
Найдем количество нулей, которыми заканчивается 100!



Третье слагаемое уже равно нулю, так как 100 5 3 = 125.
Сколько нулей в конце факториала 100?
Факториал одной сотни записывается как 100! Это произведение всех натуральных чисел до ста включительно. Иногда запись факториала имеет такой вид:
100 х 99 х 98 х 97 х … х 4 х 3 х 2 х 1
Для ответа на вопрос задачи вам не обязательно находить результат умножения. От вас ждут, чтобы вы лишь определили число нулей в конце произведения, не зная, каким именно оно будет. Для решения этой задачи потребуется сформулировать несколько правил. Одно из них вы уже знаете. Взгляните на следующее выражение.
387 000 х 12 900 = 5 027 131 727
Вам не кажется, что здесь есть что-то забавное? Ведь при перемножении двух круглых чисел, то есть тех, которые оканчиваются на нули, невозможно получить некруглое число. Это нарушило бы закон сохранения конечных нулей (закон, который я только что вывел, но, тем не менее, он является верным). Произведение всегда унаследует нулевые окончания своих составляющих. Вот несколько верных примеров этого:
10 х 10 = 100
7 х 20 = 140
30 х 400 = 12 000
Из сомножителей факториала 100 десять заканчиваются на ноль: 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100 (заканчивается на два 0). Это дает уже как минимум одиннадцать конечных нулей, которые 100! обязательно унаследует.
Предупреждение: следование только этому правилу иногда побуждает некоторых кандидатов в своем ответе заявить, что в конце факториала 100 стоят одиннадцать нулей. Такой ответ является неверным. Иногда можно умножить два числа, не заканчивающихся на ноль, и получить произведение, имеющее в конце один или несколько нулей. Вот несколько примеров этого рода:
2 х 5 = 10
5 х 8 = 40
6 х 15 = 90
8 х 125 = 1000
Все, кроме последней пары, входят в сотню составляющих факториала 100. Поэтому ваша работа не закончилась. Теперь мы подходим к закону «сосисок и булочек». Представьте себе ситуацию, когда на пикник одни люди приносят сосиски (в упаковках по десять штук), другие — булочки (упакованные по восемь штук), а некоторые — и то, и другое. Есть единственный способ, позволяющий определить, сколько хотдогов из этих продуктов можно приготовить. Сосчитайте сосиски, сосчитайте булочки и выберите меньшее число из двух.
Тот же самый закон следует использовать и отвечая на наш вопрос. Для этого надо заменить «сосиски» и «булочки» на «сомножители на 2» и «сомножители на 5».
В каждом из приведенных выше уравнений число, которое делится на 2, умножается на число, которое делится на 5. Сомножители на 2 и на 5 при их перемножении «совместно» дают идеальную десятку, что добавляет еще один ноль к общему произведению. Посмотрите на последний пример, где в конце, можно сказать, из воздуха возникает три нуля.
8 х 125 = (2 х 2 х 2) х (5 х 5 х 5)
= (2 х 5) х (2 х 5) х (2 х 5)
= 10 х 10 х 10
= 1000
Поэтому надо составить пары из двоек и пятерок. Возьмем, к примеру, число, равное 692 978 456 718 000 000.
Оно оканчивается на шесть нулей. Это означает, что его можно записать следующим образом:
692 978 456 718 х 10 х 10 х 10 х 10 х 10 х 10,
692 978 456 718 х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5) х (2 х 5).
Первая часть, 692 978 456 718, не делится на 10. В ином случае она бы оканчивалась на ноль, и можно было бы эту часть уменьшить еще в 10 раз. К тому же здесь есть шесть сомножителей, равных 10 (или 2 х 5), что соответствует шести нулям в конце числа 692 978 456 718 000 000. Ну как, убедительно?
Это дает нам надежную систему для определения количества нулей в конце любого большого числа. Выделите сомножители 2 и 5. Составьте из них пары и перемножьте их: (2 х 5) х (2 х 5) х (2 х 5) х … Число пар из двоек и пятерок равно количеству нулей в конце. Закройте глаза на все, что осталось слева.
В целом слева у вас останется двойка или пятерка, для которых не нашлось пары. Обычно это двойки. Более того, когда вы имеете дело с факториалом, это всегда двойки. (В факториалах имеется больше четных множителей, чем множителей, которые делятся на 5.) Поэтому узким местом является число пятерок. Из этого следует, что вопрос можно сформулировать по-другому: сколько раз 100! можно разделить без остатка на 5?
Эту арифметическую операцию можно легко проделать даже в голове. В диапазоне от 1 до 100 есть 20 чисел, которые делятся на пятерку: 5, 10, 15, …, 95, 100. Обратите внимание, что 25 дает 2 множителя, равные 5 (25 = 5 х 5), и к тому же в этой группе есть еще три числа, в состав которых входит 25: 50, 75 и 100. В совокупности это добавляет еще четыре пятерки, а всего их 24. 24 множителя на пять дают 24 пары с равным числом двоек, в результате чего получается 24 множителя на 10 (оставляя слева еще множество двоек, для которых не оказалось пары). Таким образом, в конце 100! будет 24 нуля.
Если вам любопытно узнать точный ответ, то значение факториала 100 равно:
93 326 215 443 944 152 681 699 238 856 266 700 490 715 968 264 381 621 468 592 963 895 217 599 993 229 915 608 941 463 976 156 518 286 253 697 920 827 223 758 251 185 210 916 864 000 000 000 000 000 000 000 000.
Факториал
ЧТО ТАКОЕ ФАКТОРИАЛ
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10 157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10 374
Факториал
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Факториал: определение
Факториал числа n — это произведение натуральных чисел от 1 до n. Обозначается n, произносится «эн-факториал».
Факториал определен для целых неотрицательных чисел. Это значит, что вот так нельзя:
Число должно быть целое и положительное:
Вычисляется факториал по формуле: путем умножения всех чисел от одного до значения самого числа под факториалом. Факторизация — это разложение функции на множители.
Мы видим, что 4! — это 3!*4
5! — это 4!*5
6! — это 5!*6
Формулы и свойства факториала
Чтобы узнать, как вычислять факториалы быстро — воспользуемся табличкой. Сохраняйте себе и решайте раньше остальных.
| 1! = 1 |
| 2! = 2 |
| 3! = 6 |
| 4! = 24 |
| 5! = 120 |
| 6! = 720 |
| 7! = 5040 |
| 8! = 40320 |
| 9! = 362880 |
| 10! = 3628800 |
| 11! = 39916800 |
| 12! = 479001600 |
| 13! = 6227020800 |
| 14! = 87178291200 |
| 15! = 1307674368000 |
| 16! = 20922789888000 |
| 17! = 355687428096000 |
| 18! = 6402373705728000 |
| 19! = 121645100408832000 |
| 20! = 2432902008176640000 |
| 21! = 51090942171709440000 |
| 22! = 1124000727777607680000 |
| 23! = 25852016738884976640000 |
| 24! = 620448401733239439360000 |
| 25! = 15511210043330985984000000 |
Факториалов в математике 9 класса — полно. Чтобы всегда быть готовым решить пример, запомните основные формулы:
С помощью формулы Стирлинга можно вычислить факториал многоразрядных чисел.
Такая формула дает результат с небольшой погрешностью.
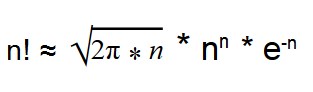 |
Рекуррентная формула
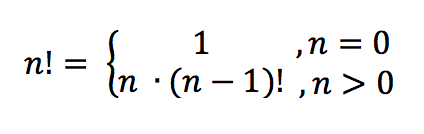 |
Для решения примеров обращайтесь к таблице.
Примеры умножения факториалов:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Примеры решений
Давайте поупражняемся и решим пару примеров.
1. Сократите дробь:
Далее сокращаем по принципу сокращения обыкновенных дробей.
2. Вычислите значение выражения с факториалом: 8! + 5!
Можно для решения факториалов воспользоваться таблицей и вычислить быстрее.
А можно потренироваться и разложить их:
8! = 1*2*3*4*5*6*7*8 = 7!*8 = 5040 * 8 = 40320
5! = 1*2*3*4*5 = 4!*5 = 120
40320 + 120 = 40440
8! + 5! = 40440
3. Вычислите значение выражения:
7! = 1*2*3*4*5*6*7 = 5! * 6 *7
Далее сокращаем все, что можем сократить (3*2=6, сокращаем числа 6) и получаем ответ.
4. Вычислите значение выражение:
Вы уже знаете, как найти факториал — раскладываем 70 и 49:
70! = 1*2*3*. *69 = 69! * 70
49! = 1*2*3*. 49! * 48
Далее сокращаем все одинаковые множители.
5. Сократите дробь:
Проводим разложение на множители при помощи формул сокращенного умножения (x+1)x(x-1) и сокращаем все одинаковые множители (x-1)!.
Если вы все еще считаете, что факториал бесполезен и не может помочь вам в жизни, то это не так. Он помогает легко вычислять вероятности (а это бывает нужно чаще, чем кажется). К тому же, комбинаторика необходима тем, кто собирается работать в IT. Поэтому решайте побольше задачек на факториалы, в мире будущего без них — никуда.