Как посчитать нср в excel
Надстройка к Excel для статистической оценки и анализа результатов полевых и лабораторных опытов
Авторы: Гончар-Зайкин П.П., к.б.н.; Чертов В.Г., к.э.н.
Нами разработан пакет программ AgCStat в виде надстройки Excel.
В настоящее время пакет включает 12 программ плюс лист с примерами подготовки данных для анализа:
3. Если первые две ссылки не работают, Вы можете скачать Эксель файл AgCStat
Анализируя список программ пакета, специалист может заметить, что некоторые программы дублируют программы стандартного Пакета анализа и даже встроенные функций. Это вызвано рядом причин.
Во-первых, неискушенному пользователю все же удобнее иметь все в одном пакете, освоить который значительно проще, чем работу со встроенными функциями.
Во-вторых, в версиях Excel младше Excel 2002 ряд функций либо отсутствуют, либо они не доступны, как, например, функции GetFisher и GetStudent – выдающих табличные значения критериев.
В-третьих, и, может быть самое главное, — это типизация. При просмотре «Примеров подготовки данных» видно, что все таблицы данных для анализов выполняются по одному типу, тогда как в стандартном Пакете анализа таблица данных для однофакторного комплекса строится по одному типу, а для двухфакторного — совсем по другому, понять который совсем не просто. По одному же типу построены и все диалоговые окна надстройки AgCSTAT (строка в меню Сервис – CXSTAT). Вся терминология, используемая в пакете, полностью соответствует терминологии принятой в отечественной литературе.
При разработке программ входящих в пакет нами использовались исключительно отечественные разработки, причем предпочтение оказывалось алгоритмам, которые в аграрных научных учреждениях приняты как стандартные.
Дадим некоторые пояснения по пакету программ.
Восстановление выпавших данных. Выбраковка делянки полевого опыта – обычное дело. Причины самые разные от градобоя до воровства и потравы. Узнать количество пропавшего в принципе нельзя, но вычислить величину, которая не нарушая статистических характеристик комплекса, восстановит его ортогональность для проведения некоторого формального анализа можно [3, 6]. Прием восстановления выпавшего данного применяется и тогда, когда некоторое данное резко отличается от соседних, однако пользоваться этим приемом следует с большой осторожностью и в купе с другими видами анализов о принадлежности данного к выборке.
Напомним, что алгоритмы Б.А. Доспехова привязаны к схеме закладки полевого опыта и повторения рассматриваются как фактор. В связи с этим, обратим внимание на то, что если в диалоговом окне «Однофакторный дисперсионный анализ по Доспехову» установить опцию «Опыт в вегетационных сосудах …», т.е. перейти к общей схеме дисперсионного анализа, то мы получим результаты, совпадающие как с результатами «по Плохинскому», так и однофакторного дисперсионного анализа пакета «Анализ данных».
В доступной нам литературе, мы не нашли четкого алгоритма трехфакторного дис-персионного анализа для количественных признаков (равномерного комплекса), но, поскольку необходимость в нем высока, разработали его сами, опираясь на алгоритмы Н.А. Плохинского [5].
Анализ опытов, связанных с изучением устойчивости растений к вредителям и болезням, а также для оценки эффективности различных химических препаратов, влияющих на устойчивость, очень часто проводится с использованием качественных признаков (больной – здоровый, заражен – не заражен и т. д.). В нашем пакете одно диалоговое окно позволяет выполнить дисперсионный анализ качественных признаков по одно, двух и трехфакторной схеме.
Программа для расчета корреляции и регрессии при парных взаимодействиях построена так, что выдает результаты регрессионного и корреляционного анализов в один прием вместе с оценкой их статистической достоверности.
Иногда исследователя интересует всего лишь величина разности средних двух выборок и ее достоверность. Эту задачу решает последняя в списке программа. Достаточно указать диапазоны, в которых находятся выборки, диапазоны могут быть как смежными, так и несмежными и даже располагаться на разных листах книги Excel.
Для установки книги надстройки на ПК достаточно иметь дискету с двумя файлами:AgCStat.xla и SetUp.exe. Вы запускаете файл SetUp.exe, а все остальное делается в автоматическом режиме. По завершению установки в списке надстроек Excel (меню Сервис — Надстройки, окно Надстройки) появится новая строка: “Agcstat”. Для начала работы с надстройкой ее нужно активизировать, установкой флажка.
Теперь в меню Сервис видим команду СХSТАТ, щелкаем по ней мышкой и на экране монитора появится диалоговое окно с перечнем программ пакета. До начала работы, советуем просмотреть примеры подготовки данных (первая строка списка). Дополнительной информации для работы с пакетом не потребуется.
Важные примечания от администратора vniioh.ru:
При использовании вышеизложенных материалов необходимо ссылаться на авторов.
Данный материал опубликован в:
Сборнике «Рациональное природопользование и сельскохозяйственное производство в южных регионах Российской Федерации» М. «Современные тетради», 2003, с.559-564 П.П. Гончар-Зайкин, В.Г. Чертов.
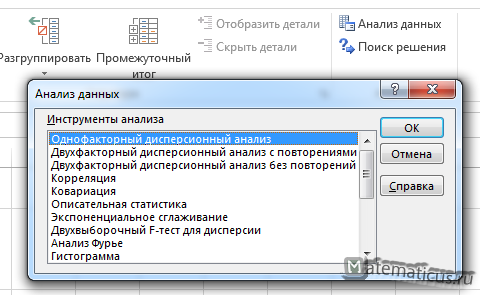
Однофакторный дисперсионный анализ в Excel
Однофакторный дисперсионный анализ изучает влияния одного фактора на анализируемый признак.
В таблицы приведены статистические данные по количеству изготовленных деталей на заводе каждым мастером в течение каждой недели.
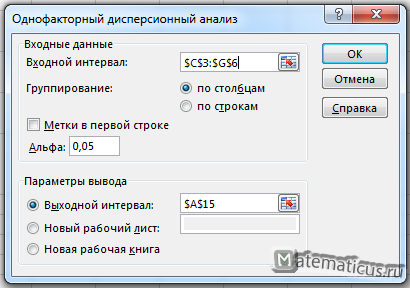
Необходимо выяснить зависимость количества изготовленных деталей от производительности мастера. Уровень значимости равен α=0.05.
| № п/п | Номер недели | Количество изготовленных деталей | ||||
| Первым мастером | Вторым мастером | Третьим мастером | Четвертым мастером | Пятым мастером | ||
| 1. | Первая неделя | 260 | 253 | 258 | 257 | 251 |
| 2. | Вторая неделя | 257 | 255 | 255 | 252 | 250 |
| 3. | Третья неделя | 259 | 250 | 254 | 253 | 255 |
| 4. | Четвёртая неделя | 254 | 254 | 260 | 257 | 251 |
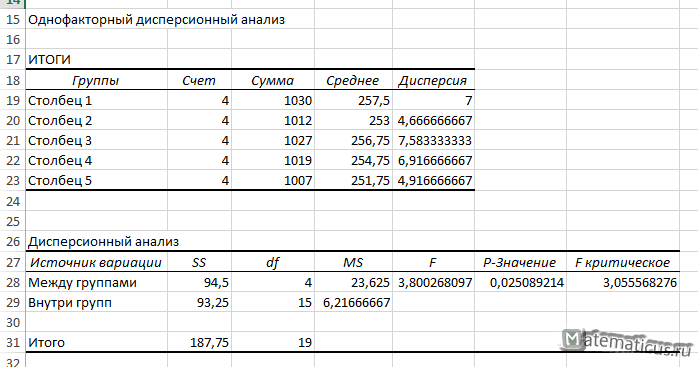
В результате получим решение в виде таблицы.
| Однофакторный дисперсионный анализ | ||||||
| ИТОГИ | ||||||
| Группы | Счет | Сумма | Среднее | Дисперсия | ||
| Столбец 1 | 4 | 1030 | 257,5 | 7 | ||
| Столбец 2 | 4 | 1012 | 253 | 4,666666667 | ||
| Столбец 3 | 4 | 1027 | 256,75 | 7,583333333 | ||
| Столбец 4 | 4 | 1019 | 254,75 | 6,916666667 | ||
| Столбец 5 | 4 | 1007 | 251,75 | 4,916666667 | ||
| Дисперсионный анализ | ||||||
| Источник вариации | SS | df | MS | F | P-Значение | F критическое |
| Между группами | 94,5 | 4 | 23,625 | 3,800268097 | 0,025089214 | 3,055568276 |
| Внутри групп | 93,25 | 15 | 6,21666667 | |||
| Итого | 187,75 | 19 | ||||
Из таблицы значения F-критерия равно Fнабл=3.8, а Fкрит=3, правосторонний интервал (3; +∞) Fнабл>Fкрит, отсюда следует, что Fнабл лежит в этом интервале, следовательно, нулевую гипотезу H0 о равенстве групповых матожиданий — отвергаем, следовательно фактор — количества изготовленных деталей зависит от признака — производительности мастера.
Найдём выборочный коэффициент детерминации:
Этот показатель говорит о том, что около половины еженедельного количества изготовленных деталей мастерами связано с номером недели.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 6
Как посчитать нср в excel
Дисперсионный анализ основан на работах знаменитого математика Р.А.Фишера (30-е годы 20 в.). Несмотря на достаточно солидный «возраст», данный метод до сих пор остается одним из основных при проведении биологических и сельскохозяйственных исследований. Идеи, положенные в основу дисперсионного анализа, широко используются во многих других методах математического анализа экспериментальных данных, а также при планировании биологических и сельскохозяйственных экспериментов.
Дисперсионный анализ позволяет:
1) сравнивать две или несколько выборочных средних;
2) одновременно изучать действие нескольких независимых факторов, при этом можно определить как эффект каждого фактора в изменчивости изучаемого признака, так и их взаимодействие;
3) правильно планировать научный эксперимент.
Изменчивость живых организмов проявляется в виде разброса или рассеяния значений отдельных признаков в пределах, которые определяются степенью биологической выравненности материала и характером взаимосвязей с условиями среды. Признаки, изменяющиеся под воздействием тех или иных причин, называют результативными.
Факторы, влияющие на степень варьирования результативного признака, делятся на:
Случайные факторы определяются естественным варьированием всех признаков биологических объектов в природе. Это неконтролируемые в опыте факторы. Они оказывают случайное влияние на результативный признак, обусловливают экспериментальные ошибки и определяют внутри каждого варианта разброс (рассеяние) признака. Этот разброс носит название внутригрупповой (случайной) дисперсии.
Таким образом, относительная роль отдельных факторов в общей изменчивости результативного признака характеризуется дисперсией и может быть изучена с помощью дисперсионного анализа или анализа рассеяния
Дисперсионный анализ основан на сравнении межгрупповой и внутригрупповой дисперсий. Если межгрупповая дисперсия не превышает внутригрупповую, значит, различия между группами имеют случайный характер. Если межгрупповая дисперсия существенно выше, чем внутригрупповая, то между изучаемыми группами (вариантами) существуют статистически значимые различия, обусловленные действием изучаемого в опыте фактора.
Из этого следует, что при статистическом изучении результативного признака при помощи дисперсионного анализа следует определить его варьирование по вариантам, повторениям, остаточное варьирование внутри этих групп и общее варьирование результативного признака в опыте. В соответствии с этим различают три вида дисперсий:
1) Общую дисперсию результативного признака (Sy 2 );
2) Межгрупповую, или частную, между выборками (Sy 2 );
3) Внутригрупповую, остаточную (Sz 2 ).
Следовательно, дисперсионный анализ – это расчленение общей суммы квадратов отклонений и общего числа степеней свободы на части или компоненты, соответствующие структуре эксперимента, и оценка значимости действия и взаимодействия изучаемых факторов по F-критерию. В зависимости от числа одновременно исследуемых факторов различают двух-, трех-, четырехфакторный дисперсионный анализ.
Сy = СV +Сp + Сz.
степени свободы для вариантов (l – 1);
степени свободы для повторений (n – 1);
случайного варьирования (n – 1)×(l – 1).
Затем вычисляют следующие показатели:
Общее число наблюдений N = l × n;
Сумму квадратов для вариантов CV = Σ V 2 / (n – 1);
Полученные суммы квадратов CV и CZ делят на соответствующие им степени свободы и получают два средних квадрата (дисперсии):
Оценка существенности разностей между средними
Полученные средние квадраты используют в дисперсионном анализе для оценки значимости действия изучаемых факторов путем сравнения дисперсии вариантов (Sv 2 ) с дисперсией ошибки (SZ 2 ) по критерию Фишера (F = SY 2 / SZ 2 ). За единицу сравнения принимают средний квадрат случайной дисперсии, который определяет случайную ошибку эксперимента.
Применение критерия Фишера позволяет установить наличие или отсутствие существенных различий между выборочными средними, но не указывает конкретных различий между средними.
2. Оценка значимости разности между средними по наименьшей существенной разности
Наименьшей существенной разностью (НСР) – является своеобразной ценой деления, разрешающей способностью опыта при оценке разности выборочных средних. Критерий НСР = t0,5 * Sd указывает предельную ошибку для разности двух выборочных средних.
Если фактическая разность больше НСР0,5 (d ≥ НСР0,5), то она значима, существенна, при d ≤ НСР0,5 – несущественна.
В многофакторном опыте изучается действие и взаимодействие нескольких факторов на изменчивость результативного признака, поэтому каждому фактору задают несколько градаций. Это позволяет изучать действие каждого из них при нескольких градациях других факторов.
Эффект взаимодействия факторов составляет ту часть общей изменчивости, которая вызвана различным действием одного фактора при разных градациях другого. В полевом опыте часто эффект от совместного применения изучаемых факторов может быть выше (синергизм) или ниже (антагонизм) суммы эффектов от раздельного применения каждого из них. В первом случае имеет место положительное, во втором – отрицательное взаимодействие факторов. Если же факторы не взаимодействуют, то эффект от совместного применения равен сумме эффектов от раздельного их применения (аддитивизм).
При дисперсионном анализе данных многофакторного опыта используют те же принципы и расчеты дисперсий, что и при однофакторном. Однако при этом усложняется математическая модель анализа.
При обработке данных двухфакторного опыта сумма квадратов расчленяется на следующие компоненты:
Соответственно с указанными компонентами расчленяется и общее число степеней свободы:
Вегетационные опыты представляют собой статистические комплексы, состоящие из нескольких независимых выборок (вариантов). Независимость сопоставляемых вариантов достигается регулярным перемещением сосудов на вагонетке. Следовательно, в вегетационных опытах обычно нет территориально организованных повторений. Поэтому в однофакторном вегетационном опыте общее варьирование результативного признака разлагается на два компонента – варьирование вариантов и случайное варьирование и общее число степеней свободы:
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ПРАКТИЧЕСКОГО ЗАДАНИЯ
ЗАНЯТИЕ 6
ОБРАБОТКА ДАННЫХ ОДНФАКТОРНЫХ ПОЛЕВЫХ ОПЫТОВ
Задача – провести дисперсионный анализ данных однофакторного полевого опыта по индивидуальному заданию согласно следующих рекомендаций:
1. Исходные цифровые данные задачи занести в таблицу 1 и определить:
3) Рассчитать средние значения в каждом из вариантов – x
4) Рассчитать общее число наблюдений в опыте – N
N = число вариантов (l) × число повторностей (п)
5) Рассчитать общую среднюю по опыту – x0
x0 = Σ x / N
*Фактические значения данных опыта – x1, x2, xn
2) Установить произвольное среднее число (начало) – А
Для этого следует вычисленное x0 округлить до целого значения.
xа – преобразованное число
xn – исходные значения в табл. 1
A – произвольное среднее число
Таблица 2 – Отклонения от произвольной средней величины – А
4) Полученные преобразованные значения (отклонения от произвольной средней) возводим в квадрат и подсчитываем сумму квадратов отклонений по вариантам и по повторениям (табл. 3):
Таблица 3 – Квадраты преобразованных значений
5) Затем вычисляют суммы квадратов отклонений в следующей последовательности:
Корректирующий фактор (поправку) Скор = (Σ xа)2 / N;
Общую сумму квадратов Cy = Σ (xа2) – Cкор;
Сумму квадратов для повторений Cp = Σ P2 / (l –Cкор);
Сумму квадратов для вариантов CV = Σ V2 / (n – 1);
6) После вычисления сумм квадратов отклонений, заполняется таблица результатов дисперсионного анализа (табл. 4)
Таблица 4 – Результаты однофакторного дисперсионного анализа
Вариантов: Sv2 = CV / l – 1;
Остаточное: SZ2 = CZ / (n – 1)?(l – 1)
*Теоретическое значение F05 находят по таблице (см.прил. ), исходя из числа степеней свободы для дисперсий вариантов (числитель) и числа степеней свободы для дисперсии остатка (знаменатель).
Если Fфакт. ≥ F05(табл.) в опыте есть существенные различия по вариантам, тогда необходимо определить между какими вариантами наблюдаются существенные отличия (оценка существенности частных различий по НСР).
7) Для оценки существенности частных различий вычисляются следующие величины:
— обобщенную ошибку средней: Sx = √ S2 / n
— ошибку разности средних: Sd = √ 2S2 / n
Критерий НСР = t0,5*Sd указывает предельную ошибку для разности двух выборочных средних. Если фактическая разность больше НСР0,5 (d ≥ НСР0,5), то она значима, существенна, при d ≤ НСР0,5 – несущественна.
Значения t – критерия для принятого уровня значимости и числа степеней свободы остаточной дисперсии берут из таблицы (см.прил.1).
Полученные результаты статистической обработки заносятся в итоговую табл. 5:
Таблица 5 – Итоговая таблица дисперсионного анализа
8) На основании полученных данных однофакторного полевого опыта сделать письменные выводы об эффективности того или иного применяемого в опыте агротехнического приема (градации фактора).
Задания для обработки данных однофакторного полевого опыта методом дисперсионного анализа:
1. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности нормы высева (млн. всхожих зерен/га) на урожайность (ц/га) озимой ржи (почва – дерново-подзолистая):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 4 млн. | 21,3 | 23,4 | 23,5 | 22,0 |
| 2 | 5 млн. | 25,5 | 24,4 | 24,0 | 26,3 |
| 3 | 6 млн. | 18,9 | 19,6 | 20,5 | 19,9 |
2. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности сроков посева на урожайность (ц/га) яровой пшеницы (почва – чернозем обыкновенный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 15-20 мая | 17,4 | 15,9 | 16,5 | 22,0 |
| 2 | 20-25 мая | 21,0 | 20,4 | 19,5 | 26,3 |
| 3 | 25-30 мая | 20,4 | 19,5 | 18,0 | 19,9 |
3. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности доз азотного удобрения на урожайность (ц/га) ячменя (почва – серая лесная):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | N30 | 17,9 | 15,5 | 15,9 | 19,1 |
| 2 | N50 | 19,3 | 18,7 | 19,1 | 19,0 |
| 3 | N70 | 21,3 | 20,5 | 21,0 | 21,7 |
| 4 | N90 | 25,4 | 27,1 | 26,4 | 26,5 |
4. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности полного минерального удобрения на урожайность (ц/га) картофеля (почва – чернозем выщелоченный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | N30P30K60 | 170 | 184 | 180 | 194 |
| 2 | N50P60K90 | 238 | 214 | 219 | 226 |
| 3 | N70P90K120 | 205 | 209 | 197 | 189 |
5. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности сортов на урожайность (ц/га) овса (почва – чернозем обыкновенный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | Сельма | 25,6 | 24,4 | 24,5 | 28,1 |
| 2 | Таежник | 26,9 | 27,1 | 25,4 | 25,9 |
| 3 | Саян | 34,5 | 30,9 | 32,4 | 31,7 |
6. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности ширины междурядий на урожайность зеленой массы кукурузы (ц/га) (почва – светло-серая лесная):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 45см | 425 | 411 | 397 | 408 |
| 2 | 90см | 560 | 587 | 544 | 559 |
| 3 | 120см | 490 | 484 | 471 | 482 |
7. Обработать методом дисперсионного анализа данные полевого опыта по изучению сроков внесения азотного удобрения под озимую рожь на урожайность (ц/га) картофеля (почва – серая лесная):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | до посева | 17,1 | 17,8 | 17,4 | 18,0 |
| 2 | в подкормку весной | 24,3 | 27,4 | 25,0 | 27,0 |
| 3 | в фазу выхода в трубку | 20,1 | 19,3 | 20,9 | 21,6 |
8. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности глубины основной обработки на урожайность (ц/га) яровой пшеницы (почва – чернозем выщелоченный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 20-22 см | 28,4 | 29,7 | 25,6 | 26,3 |
| 2 | 25-27 см | 24,4 | 21,9 | 25,7 | 22,1 |
| 3 | 30-32 см | 18,7 | 19,4 | 17,1 | 17,7 |
9. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности доз органических удобрений на урожайность (ц/га) капусты (почва – темно-каштановая):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 20 т/га | 311 | 340 | 338 | 325 |
| 2 | 40 т/га | 347 | 338 | 356 | 340 |
| 3 | 60 т/га | 380 | 377 | 365 | 388 |
| 4 | 80 т/га | 450 | 468 | 470 | 458 |
10. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности способа обработки почвы на урожайность (ц/га) яровой пшеницы (почва – чернозем обыкновенный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 20-22см | 14,7 | 13,2 | 17,4 | 17,1 |
| 2 | 30-32см | 11,9 | 12,5 | 12,7 | 12,4 |
| 3 | 20-22см | 20,3 | 17,4 | 19,3 | 19,7 |
| 4 | 30-32см | 16,2 | 16,0 | 15,9 | 16,9 |
11. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности предшественников на урожайность (ц/га) яровой пшеницы (почва – темно-каштановая):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | чистый пар | 19,3 | 19,9 | 18,8 | 19,7 |
| 2 | пар кулисный | 23,7 | 22,1 | 22,5 | 23,5 |
| 3 | донник 2 год использов. | 15,6 | 15,8 | 14,3 | 14,7 |
12. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности доз полного минерального удобрения на содержание белка (%) в зерне ячменя (почва – чернозем выщелоченный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | N30P60K40 | 15,9 | 12,6 | 12,7 | 13,0 |
| 2 | N45P75K55 | 13,8 | 13,4 | 13,6 | 12,9 |
| 3 | N60P90K70 | 15,8 | 14,9 | 15,7 | 15,9 |
13. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности видов органических удобрений на урожайность кукурузы (ц/га) (почва – темно-серая лесная):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | навоз | 55,7 | 57,8 | 53,0 | 55,9 |
| 2 | сидерат | 48,4 | 49,3 | 45,9 | 49,0 |
| 3 | торфокомпост | 52,4 | 50,9 | 51,2 | 51,5 |
14. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности гербицидов на урожайность (ц/га) яровой пшеницы (почва – чернозем обыкновенный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | Ковбой | 29,3 | 27,3 | 28,2 | 26,4 |
| 2 | ПумаСупер | 30,2 | 29,4 | 29,7 | 28,1 |
| 3 | Логран | 34,4 | 33,3 | 35,2 | 33,0 |
15. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности предшественников на урожайность озимой ржи (ц/га) (почва – дерново-подзолистая):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | клевер | 19,6 | 20,8 | 19,2 | 19,4 |
| 2 | горох+овес | 17,8 | 18,4 | 18,1 | 16,3 |
| 3 | рапс | 23,3 | 25,6 | 23,3 | 23,7 |
16. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности числа предпосевных культиваций на урожайность (ц/га) яровой пшеницы (почва – чернозем обыкновенный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 1 | 20,4 | 17,3 | 17,9 | 19,5 |
| 2 | 2 | 21,0 | 20,5 | 20,3 | 19,8 |
| 3 | 3 | 22,9 | 23,4 | 23,1 | 23,9 |
17. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности способа обработки почвы на запасы продуктивной влаги (мм) в слое 0-20 см (почва – чернозем обыкновенный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | отвальная | 18,7 | 19,4 | 19,0 | 19,9 |
| 2 | плоскорезная | 24,3 | 24,3 | 26,7 | 22,6 |
| 3 | нулевая | 20,1 | 20,7 | 21,3 | 20,8 |
18. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности дозы азотного удобрения на фоне фосфорно-калийных удобрений на урожайность (ц/га) яровой пшеницы (почва – чернозем выщелоченный):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | N60P60K60 | 14,4 | 15,6 | 13,2 | 13,9 |
| 2 | N90P60K60 | 17,3 | 16,4 | 16,2 | 16,9 |
| 3 | N120P60K60 | 24,3 | 25,8 | 25,7 | 22,0 |
19. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности доз азотно-калийных удобрений на урожайность зеленой массы (ц/га) кукурузы (почва – серая лесная):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | N45K60 | 311 | 298 | 304 | 319 |
| 2 | N60K75 | 380 | 371 | 377 | 394 |
| 3 | N75K90 | 411 | 431 | 438 | 449 |
20. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности доз извести на уровень каталитической активности (см3/1г) дерново-подзолистой почвы:
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 1 т/га | 3,1 | 2,8 | 3,0 | 3,1 |
| 2 | 2 т/га | 4,9 | 4,7 | 4,9 | 4,9 |
| 3 | 3 т/га | 5,1 | 5,0 | 5,0 | 4,9 |
21. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности доз органических удобрений на скорость продуцирования углекислого газа дерново-подзолистой почвы (г/м2 * сутки):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 10 т/га | 4,3 | 3,9 | 3,7 | 3,7 |
| 2 | 20 т/га | 5,6 | 5,9 | 6,7 | 6,1 |
| 3 | 30 т/га | 7,9 | 7,7 | 8,4 | 7,9 |
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 15-20 мая | 19,6 | 17,1 | 17,8 | 17,9 |
| 2 | 20-25 мая | 20,0 | 21,3 | 21,4 | 21,5 |
| 3 | 25-30 мая | 24,3 | 25,7 | 25,5 | 26,8 |
23. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности сроков мульчирования сидеральной массой почвы участка на запасы продуктивной влаги (мм) в слое почвы 0-20 см:
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 15 июля | 45,0 | 51,0 | 47,0 | 49,0 |
| 2 | 15 августа | 41,0 | 44,0 | 43,0 | 47,0 |
| 3 | 15 сентября | 31,0 | 30,0 | 35,0 | 36,0 |
24. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности нормы высева ярового рапса на содержание переваримого протеина (%) в зеленой массе рапса:
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 2,5 млн. | 16,7 | 17,0 | 17,1 | 16,8 |
| 2 | 3,5 млн. | 17,1 | 17,6 | 17,9 | 17,1 |
| 3 | 4,5 млн. | 14,9 | 14,7 | 14,8 | 14,9 |
25. Обработать методом дисперсионного анализа данные полевого опыта по изучению эффективности сроков заделки ярового рапса на содержание подвижного органического вещества в дерново-подзолистой почве (С мг/100г):
| № | Варианты | повторения | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 1 | 15 июля | 31,4 | 30,7 | 32,3 | 33,4 |
| 2 | 15 августа | 31,9 | 33,7 | 30,4 | 32,9 |
| 3 | 15 сентября | 47,8 | 45,3 | 46,7 | 47,7 |
© ФГОУ ВПО Красноярский государственный аграрный университет