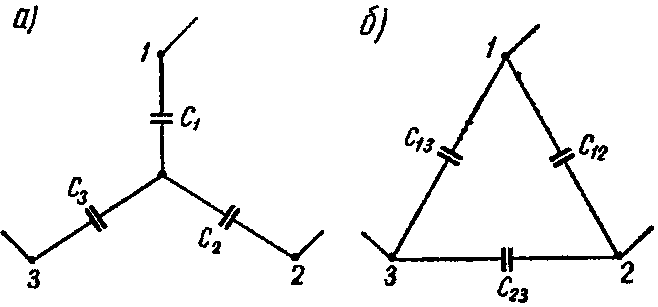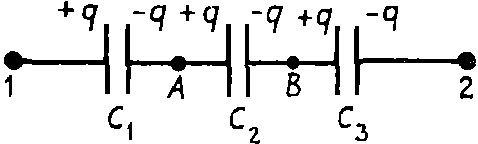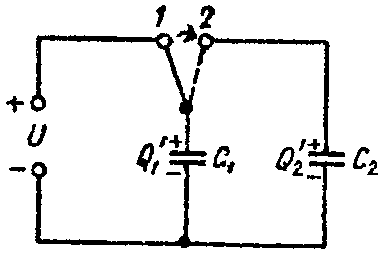Как посчитать напряжение на конденсаторе

Конденсатор в цепи постоянного тока

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление.

Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами.

Заряд конденсатора от источника постоянной ЭДС

Разряд конденсатора через сопротивление

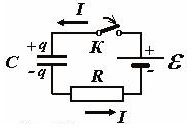
Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС (батареи):

Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора.
По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом:

При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.

Во время зарядки конденсатора, напряжение на нем изменяется по закону

где величину

называют постоянной времени RC-цепи или временем зарядки конденсатора.
Вообще говоря, согласно уравнению выше, заряд конденсатора бесконечно долго стремится к величине ЭДС, поэтому для оценки времени заряда конденсатора используют величину
— это время, за которое напряжение на конденсаторе достигнет значения 99,2% ЭДС.
Заряд на конденсаторе:

Энергия, запасенная в конденсаторе:

Работа, выполненная источником ЭДС:

Источник

формулы для конденсаторов

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме.

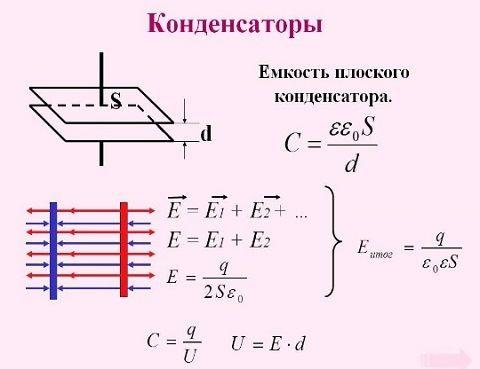
Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU 2 /2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

Источник

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

2. Емкость плоского конденсатора

S – поверхность каждой пластины конденсатора;

d – расстояние между ними;

ε_r – диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4 π ⋅ с 2 ⋅ 10 − 7 ≈ 8,85418782 ⋅ 10 − 12 Ф м – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

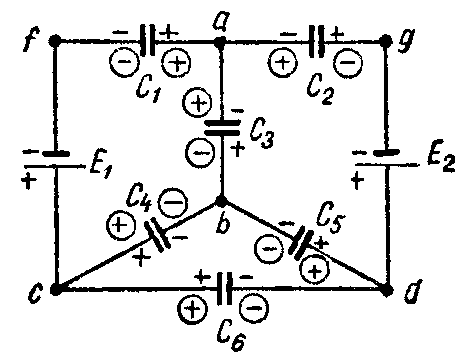
5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

осуществляется по формулам:

6. Энергия электростатического поля конденсатора:

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость – это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ – φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

Воспользовавшись формулой напряжения на конденсаторе

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

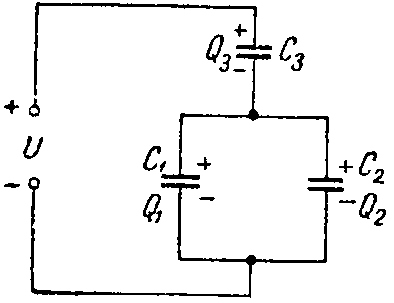
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

эквивалентная емкость всей цепи равна

Заряд на эквивалентной емкости

Q = C·U = 120·10 –6 ·240 = 288·10 –4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10 –4 Кл; напряжение на этом конденсаторе

Напряжение на конденсаторах C₁ и C₂ равно

их заряды имеют следующие значения

Энергии электростатического поля конденсаторов равны

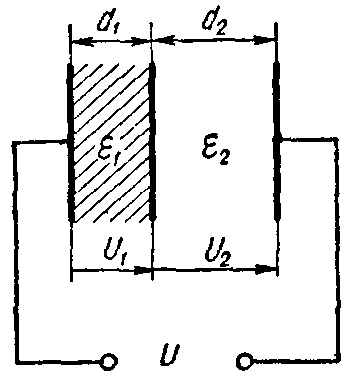
Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Напряжения на каждом слое будут равны

Напряженности электростатического поля в каждом слое

Здесь U’_np – общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»_np – общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Энергия заряженного плоского конденсатора равна

где С₁ – емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из

где C₂ – емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

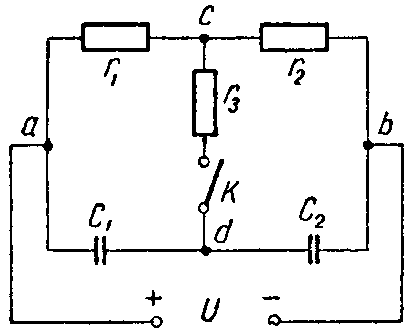
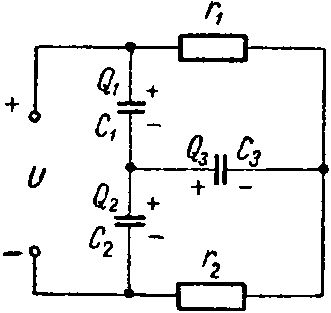
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

а через сопротивление r₃ ток не протекает.

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

Аналогично напряжение на втором конденсаторе равно

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

По второму закону Кирхгофа имеем

Q ′ 1 5 ⋅ 10 − 6 − Q ′ 2 120 ⋅ 10 − 6 = 0. ( 2 )

Решая уравнения (1) и (2), найдем

Напряжение на зажимах конденсаторов станет равным

Энергия обоих конденсаторов будет равна

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10 –6 – 62,5·10 –6 = 1500·10 –6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

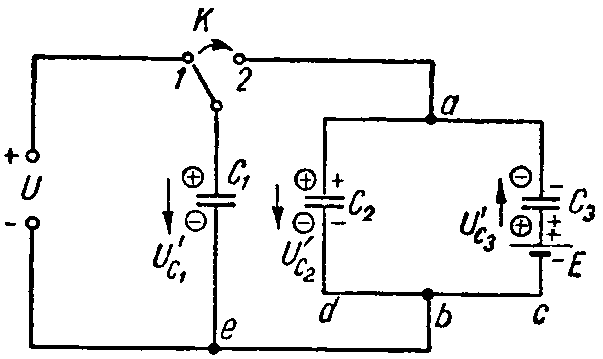
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для контура 2ebda2

Уравнения (1) – (3), после подстановки числовых значений величин, примут вид

Решая совместно уравнения (4) – (6), получим

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

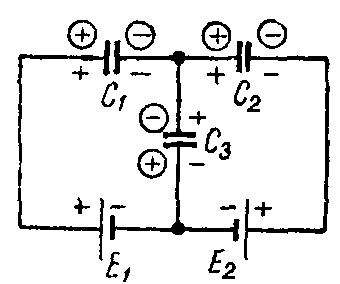
Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ – противоположна выбранной.

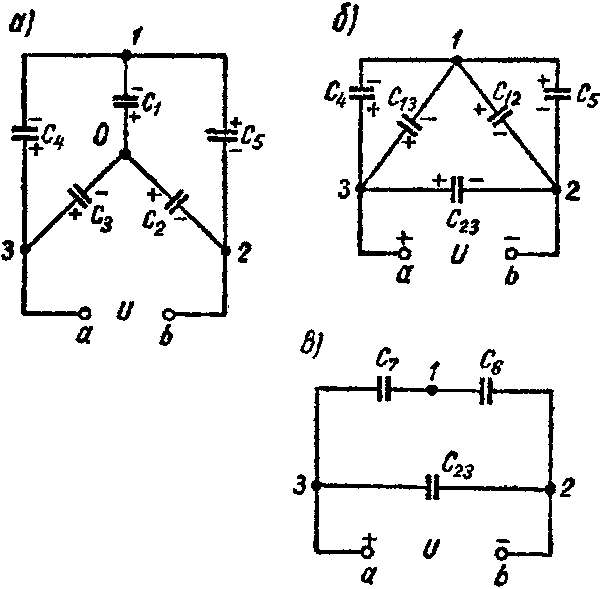
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

Таково же напряжение и на конденсаторах C₄ и C₁₃

Напряжение на конденсаторе C₆ равно

По закону сохранения электричества для узла 1 схем 8, а и б имеем

а напряжение на конденсаторе, емкостью C₁ составляет

Далее находим напряжения и заряды на остальных конденсаторах

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 = 0 ; ( 3 )

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 = 0 ; ( 4 )

Система уравнений (1) – (5) – содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

E 1 = U C 1 + U C 4 − U C 3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

E 2 = U C 5 − U C 3 + U C 2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Через сопротивления протекает ток

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

Решив эту систему уравнений, найдем, что

Цепи с конденсаторами, Конденсатор в цепи постоянного тока, Расчет цепи конденсаторов, параллельное соединение конденсаторов, последовательное соединение конденсаторов

Источник

Заряд и разряд конденсатора

Значение диэлектрика

Кроме общего размера обкладок и расстояния между ними, существует ещё один параметр, влияющий на ёмкость — используемый тип изолятора. Фактор, по которому определяется способность диэлектрика повышать ёмкость конденсатора в сравнении с вакуумом, называется диэлектрической проницаемостью и описывается для разных материалов постоянной величиной от 1 и до бесконечности (теоретически):

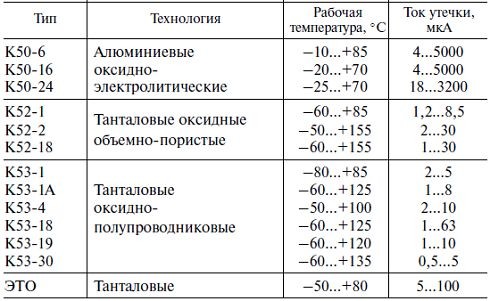
Кроме конденсаторов с твёрдым диэлектриком (керамических, бумажных, плёночных) существуют также электролитические. В последних используют алюминиевые или танталовые пластины с оксидным изолирующим слоем в качестве одного электрода и раствор электролита в качестве другого.

Энергия, которую способны накопить большинство конденсаторов, обычно невелика — не больше сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому конденсаторы не могут заменить, например, аккумуляторные батареи в качестве источника питания. И хотя они способны эффективно выполнять только одну работу (сохранение заряда), их применение весьма многообразно в электрических цепях. Конденсаторы используются как фильтры, для сглаживания сетевого напряжения, в качестве устройств синхронизации и для других целей.

Синтаксис

Для пользователей XMPP клиентов, используется команда

где ключи это известные параметры, параметра=значение, разделенные точкой с запятой

Обязателен ключ key=razryad при расчете разаряда конденсатора

и zaryad при расчете заряда

Так как при других параметрах ключах будут рассчитываться совершенно другие формулы. Например баллистического движения или давления над уровнем моря.

Заметьте, чем данный калькулятор отличается от других:

Во первых: данные можно вводить не переводя из наноФарад в Фарады, а килоОмы в Омы. Если уж заданы параметры в единицах измерения то так и пишите. Если не напишите то считается что данные заданы в основным единицах СИ ( то есть метр, Фарад, Ом)

Во вторых: Расчет ведётся по тем параметрым которые можно рассчитать зная исходные.Это очень удобно, когда нужно рассчитать любой из параметров в формуле, когда известны все остальные. Другие известные калькуляторы могут рассчитывать только по определенному алгоритму и только в одну сторону.

Разряд конденсатора

После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.

В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.

Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.

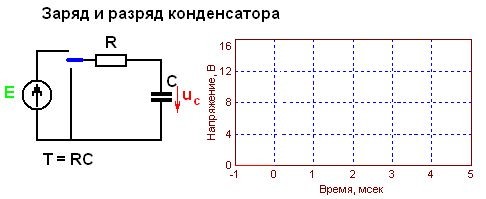
Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.

Продукт RC (сопротивление, умноженное на емкость) формирует временную константу ? (тау). За один ? конденсатор заряжается или разряжается на 63%. За пять ? конденсатор заряжается или разряжается полностью.

Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:

Заряд конденсатора. Ток

По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.

Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.

В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.

Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.

Формула

Нахождение тока конденсаторного заряда происходит по формуле, представленной ниже. Измеряется он в фарадах, что равно кулону или вольту.

Формула нахождения заряда конденсатора

В целомэто элемент электросети, накапливающий и сохраняющий напряжение в ней. Бывает разного типа и размера, к примеру, электролитическим, керамическим и танталовым. Состоит, в основном, из нескольких токопроводящих обкладок с диэлектриком. Его емкость зависит от размеров диэлектрика и заполнителя между обкладками. Заряжается благодаря электричеству. Определить ток конденсаторного заряда можно измерительными приборами и формулой.

Устройство и принцип работы

В простейшем варианте конструкция состоит из двух электродов в форме проводящих пластин (называемых обкладками), разделённых диэлектриком, толщина которого ничтожно мала по сравнению с размерами обкладок. Практически применяемые радиоэлектронные компоненты содержат много слоёв диэлектрика и электродов. В качестве обозначения конденсатора на схеме используются два параллельных отрезка с пространством между ними. Они символизируют металлические пластины обкладок физического прибора, электрически разделённые между собой.

Многие считают Майкла Фарадея автором изобретения, но на самом деле это не так. Но он сделал главное — продемонстрировал первые практические примеры и способы использования этого прибора для хранения электрического заряда в своих экспериментах. Благодаря Фарадею человечество получило способ измерять возможность накапливать заряд. Эта величина называется ёмкостью и измеряется в Фарадах.

Работу конденсатора можно проиллюстрировать на примере событий, проходящих во вспышке цифровой фотокамеры за отрезок времени между нажатием кнопки и тем моментом, когда вспышка погаснет. Основой электронной схемы этого осветительного устройства является конденсатор, в котором происходит следующее:

Определение заряда

Определить, заряжен ли проводник, можно специальным измерительным прибором. К примеру, сделать это можно при помощи индикаторной отвертки. При разряде избыточные виды электронов, имеющих левую пластину, будут перемещены через некоторое время по проводам к правой части пластины, то есть они будут смещены к местам, где их недостаточно.

Обратите внимание! Когда число электронов будет одинаковым, то разряд прекратится и проводная энергия вместе с сопротивлением исчезнет. Использование измерительного оборудования для определения конденсаторного заряда

Использование измерительного оборудования для определения конденсаторного заряда

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как видите, здесь нет ничего сложного

Относительная диэлектрическая проницаемость

Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.

Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.

Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.

Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.

Бумага – от 2.5 до 3.5

Стекло – от 3 до 10

Порошки оксидов металлов – от 6 до 20

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины – обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

Здесь \sigma– это поверхностная плотность заряда: \sigma = \frac, а \varepsilon – диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

Но направления векторов разные – внутри конденсатора вектора направлены в одну сторону, а вне – в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

А какая же будет величина напряженности вне конденсатора? А все просто – слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0

От чего зависит емкость

Емкость это свойство накопления и удержания электрозаряда. Чем она больше, тем больше заряд, увеличивающий вместимость сосуда с газовым баллоном. Она зависит от того, какова форма и размер электродов. Также зависит от того, какое расположение и свойство имеет диэлектрик, разделяющий электрод. Есть плоский конденсаторный источник с параллельной и цилиндрической пластиной.

Имеет не только специально предусмотренное устройство, но и несколько проводников, которые разделены при помощи диэлектрика. Емкость существенно влияет на электротехнические установки переменного тока. К примеру, источник с определенной емкостью имеется электрический провод с живым электрическим кабелем, жилой и металлической кабельной оболочкой.

От чего зависит емкость

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

Здесь у нас d – это расстояние между пластинами конденсатора, а q – заряд конденсатора. Подставим эту формулу в выражение для емкости:

Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить \varepsilon = 1.

Для запасенной энергии конденсатора справедливы следующие выражения:

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!

Источник