Как посчитать медиану в эксель
Функция МЕДИАНА
В этой статье описаны синтаксис формулы и использование функции МЕДИАНА в Microsoft Excel.
Описание
Возвращает медиану заданных чисел. Медиана — это число, которое является серединой множества чисел.
Синтаксис
Аргументы функции МЕДИАНА описаны ниже.
Число1, число2. Аргумент «число1» является обязательным, последующие числа необязательные. От 1 до 255 чисел, для которых требуется определить медиану.
Замечания
Если в наборе имеется ряду чисел, медиана вычисляет среднее значение двух чисел в середине. См. вторую формулу в примере.
Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.
Учитываются логические значения и текстовые представления чисел, которые непосредственно введены в список аргументов.
Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, то такие значения пропускаются; однако ячейки, которые содержат нулевые значения, учитываются.
Аргументы, которые являются значениями ошибки или текстами, не преобразуемыми в числа, приводят в возникновению ошибок.
Примечание: Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Расчет медианой группы чисел
Предположим, что вы хотите узнать, что такое средний балл в распределении о оценкам учащихся или в образце данных для контроля качества. Чтобы вычислить медиану группы чисел, используйте функцию МЕДИАНА.
Функция МЕДИАНА измеряет центральную тенденцию, которая является центром множества чисел в статистическом распределении. Существует три наиболее распространенных способа определения центральной тенденции:
Среднее значение — это среднее арифметическое, которое вычисляется путем сложения набора чисел с последующим делением полученной суммы на их количество. Например, средним значением для чисел 2, 3, 3, 5, 7 и 10 будет 5, которое является результатом деления их суммы, равной 30, на их количество, равное 6.
Медиана — это число, которое является серединой множества чисел, то есть половина чисел имеют значения большие, чем медиана, а половина чисел имеют значения меньшие, чем медиана. Например, медианой для чисел 2, 3, 3, 5, 7 и 10 будет 4.
Мода — это число, наиболее часто встречающееся в данном наборе чисел. Например, модой для чисел 2, 3, 3, 5, 7 и 10 будет 3.
При симметричном распределении множества чисел все три значения центральной тенденции будут совпадать. При смещенном распределении множества чисел значения могут быть разными.
Снимки экрана в этой статье получены в Excel 2016. Если вы используете другую версию, интерфейс может немного отличаться, но функции будут такими же.
Пример
Чтобы этот пример проще было понять, скопируйте его на пустой лист.
Откройте пустую книгу или лист.
Выберите пример ниже.
Примечание: Не выделяйте заголовки строк или столбцов.
Как в Excel посчитать медиану
Чтобы рассчитать медиану в Эксель, можно воспользоваться встроенной функцией МЕДИАНА. Попытаемся разобраться, что такое медиана и рассмотрим методы ее вычисления для выборки или распределения случайных чисел.
Медиана выборки
Итак, медиана представляет собой число, которое выражает середину множества определенного ряда чисел. Таким образом, половина чисел указанного ряда будет больше значения вычисленной медианы, а вторая половина числового ряда – меньше. Для того чтобы определить медиану, нужно отсортировать числовые значения выборки. В итоге медианой выборки цифр 2, 2, 3, 5, 6, 7, 8 будет 5. В данном случае выборка состоит из семи значений – три цифры больше полученной медианы и три – меньше.
Важно! Если выборка состоит четного количества целых цифровых значений, то медиана будет представлена в виде десятичной дроби. Так, медиана выборки ряда 2, 2, 3, 5, 6, 7, 8, 10 составляет 5,5.
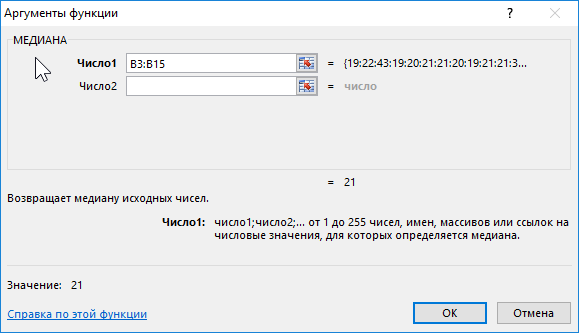
Вычисление медианы выборке через возможности Excel осуществляется при помощи соответствующей функции МЕДИАНА. В скобках формулы можно проставить до 255 значений, из которых необходимо вычислить медиану.
Функция МЕДИАНА с выборкой из семи чисел
Медиана не всегда совпадает со средним цифровым значением из представленного ряда. Как правило, совпадение бывает только при симметричном тождестве относительно среднего показателя.
Обратите внимание! Медиана – это не то же самое, что среднее значение. Средний показатель выборки чисел 2, 2, 3, 5, 6, 7, 300 соответствует значению 46,42857, медиана при этом все еще равна 5, так как соотношение чисел больше 5 и меньше не изменилось.
Медиана непрерывного распределения
Теперь рассмотрим расчет медианы в случае непрерывного распределения. Показатель медианы – это результат решения функции распределения случайных непрерывных числовых величин. Если показатель функции распределения (т.е. функция плотности) известен, то значение медианы можно вычислить по такой формуле:
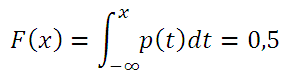
При решении данного уравнения аналитическим методом при логнормальном распределении LnN (µ; σ; 2), значение медианы модно вычислить благодаря формуле =EXP (µ). При условии, что µ=0, медиана будет равна 1. В программе Excel результат медианы для логнормального распределения, представленная формулой LnN (0; 1) вычисляется через функцию =ЛОГНОРМ.ОБР (0,5; 0; 1).
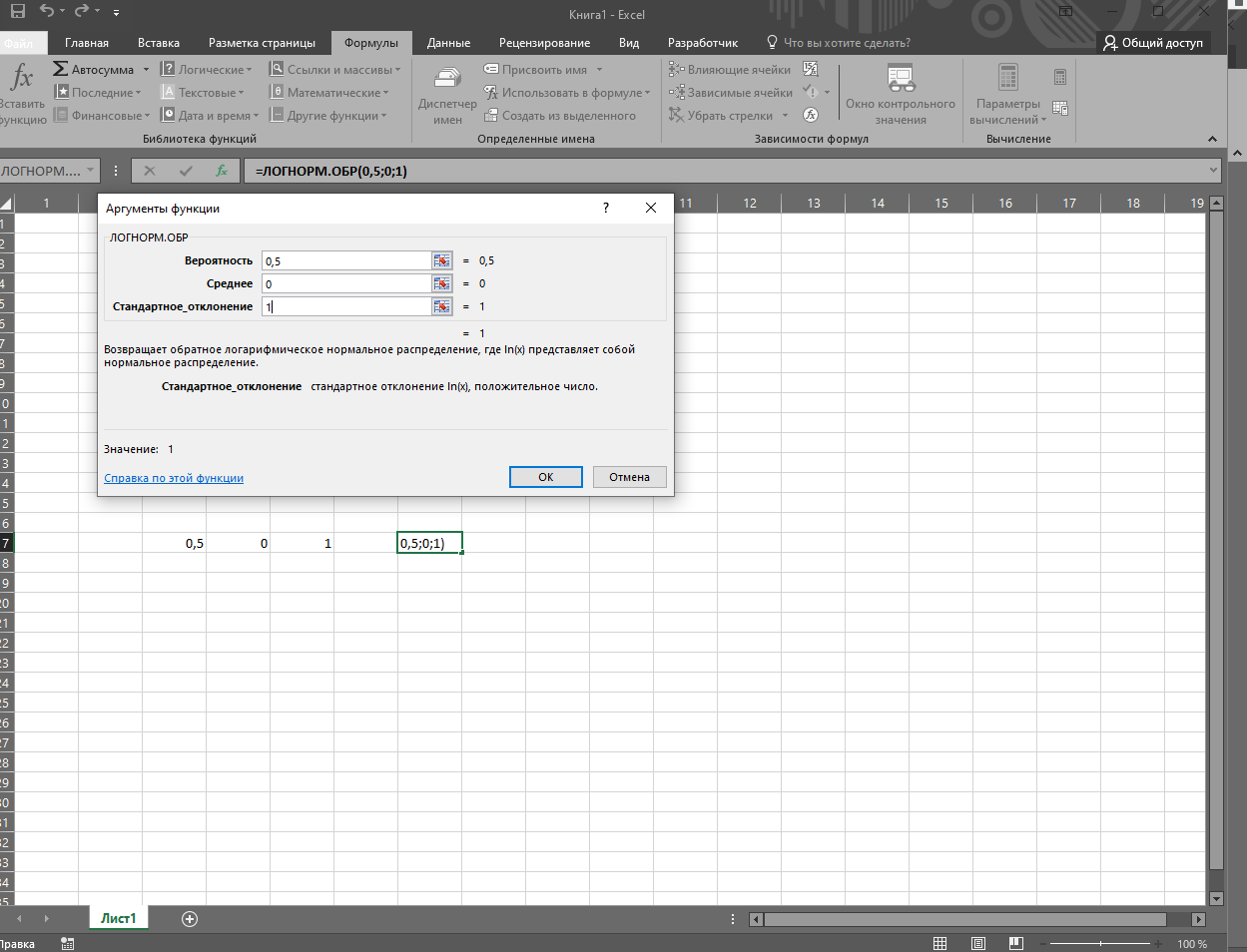
Функция МЕДИАНА
Применяя функцию МЕДИАНА в Эксель, можно вычислить значение середины числового множества. Синтаксическое выражение представляет собой формулу =МЕДИАНА (число 1; [число 2]…). Аргументы «Число 1», «Число 2» и так далее до «Число 255». Первое значение – это обязательное значение, последующие – необязательные, но именно они помогают вычислить медиану.
Следует отметить! В качестве аргументов могут использоваться не только числовые значение, но и ссылки, имена, массивы. Если ссылка или массив частично представлены в виде текста или в выборке есть пустые ячейки, то эти значения не учитываются в процессе вычислений. Использование текстового формата в аргументах приводят к ошибкам в работе функции.
Среднее значение ряда чисел
Рассмотрим вариант расчета средних значений определенного ряда чисел. Например, это может быть средняя температура воздуха в конкретный день года, выполнение поставленных задач сотрудниками и так далее. Для выполнения данного вычисления потребуются три важных параметра:
Указанные параметры при симметричном распределении числового ряда своих значений не меняют, а при асимметричном распределении они могут меняться.
Вычисление значений непрерывного ряда
При определении среднего значения непрерывного числового ряда необходимо осуществить определенный порядок действия:
Среднее взвешенное значение
Здесь случае придется использовать несколько функций – СУММ и СУММПРОИЗВ. Попробуем рассчитать среднюю стоимость единицы товара при наличии трех товаров и количества проведенных продаж. Синтаксис формулы выглядит таким образом: =СУММПРОИЗВ (R[-3]C : R[-3]C[1] : R[-1]C[1]) / СУММ (R[-3]C[1] : R[-1]C[1]). После выполнения данной функции получим среднее значение стоимости одной единицы товара 184,5238095
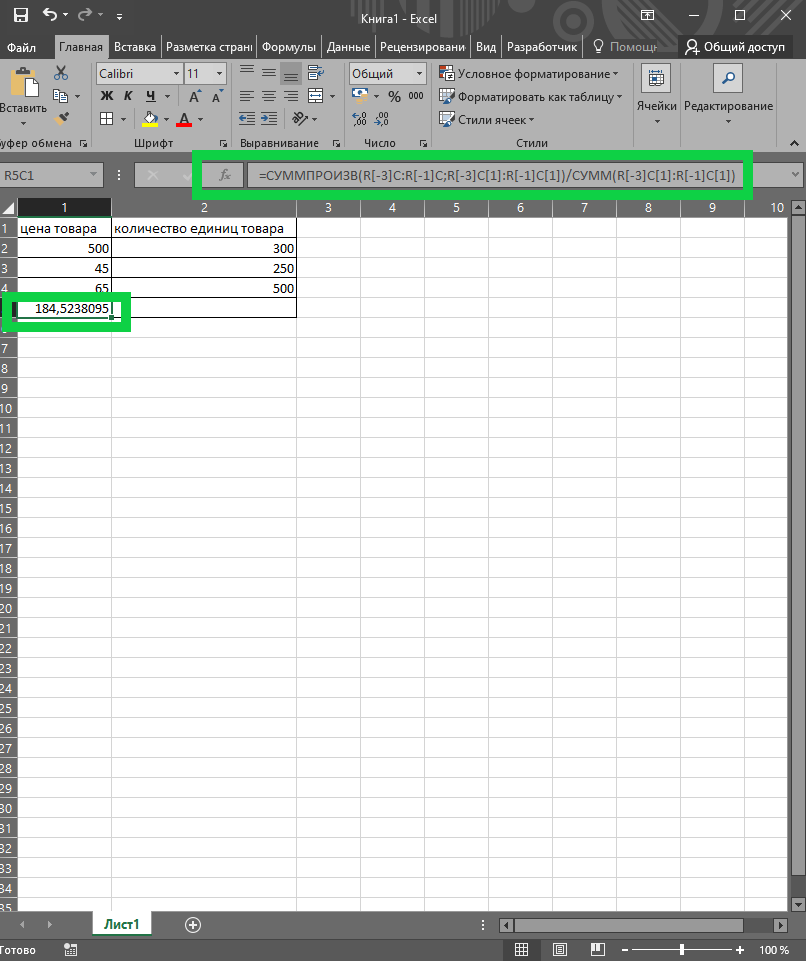
Вычисление без учета нулевых значений
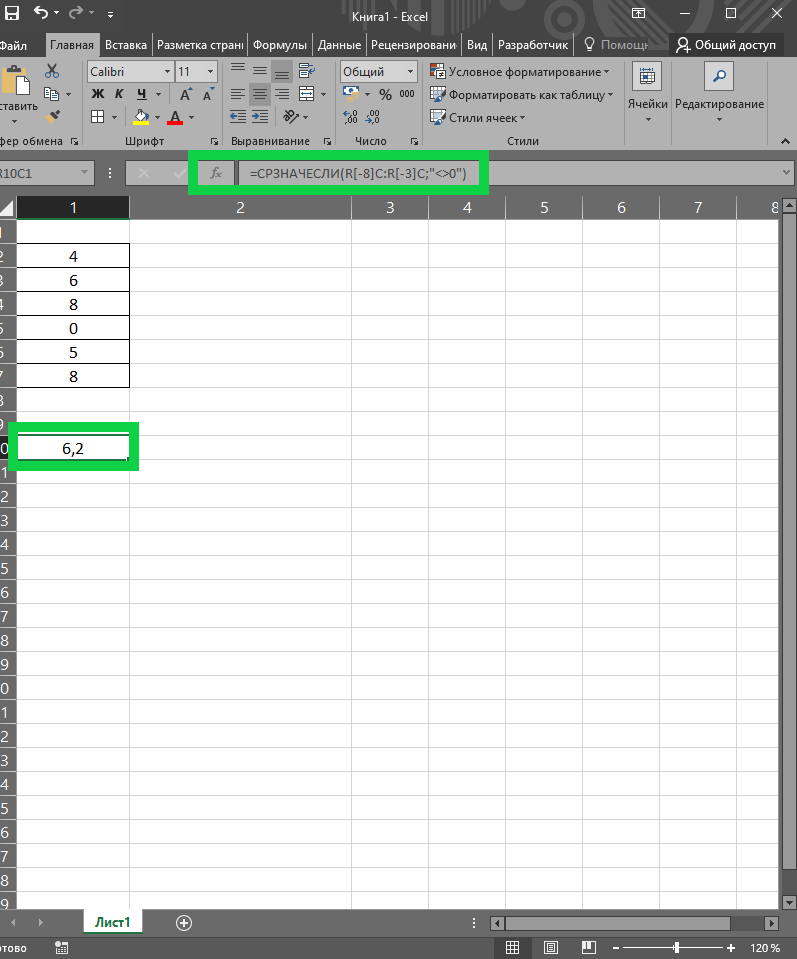
Чтобы в процессе вычислений не учитывались нулевые значения, необходимо воспользоваться двумя функциями – ЕСЛИ и СРЗНАЧ. Рассмотрим пример. В представленном числовом ряду 4, 6, 8, 0, 5, 8 необходимо найти среднее значение, но с условием исключения нулевого значения. Функция будет иметь такой синтаксис: =СРЗНАЧЕСЛИ (А2:А7; “<>0”). В итоге результат функции без нуля будет равен 6,2.
Полезные видео
Ознакомиться с основными принципами вычисления медианы в программе Excel можно, просмотрев несколько обучающих роликов в YouTube
Функция МЕДИАНА в Excel для выполнения статистического анализа
Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.
Примеры использования функции МЕДИАНА в Excel
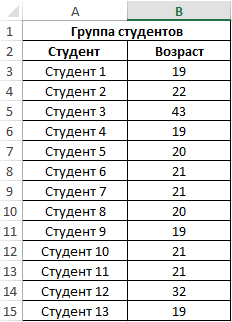
Пример 1. При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.
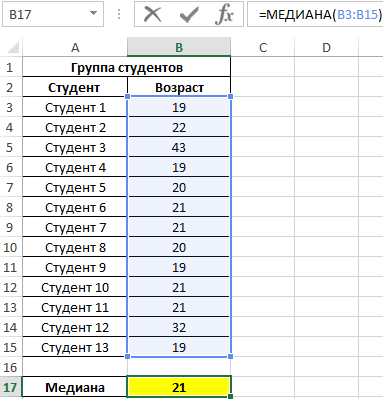
Формула для расчета:
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.
Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения
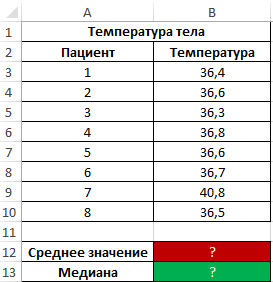
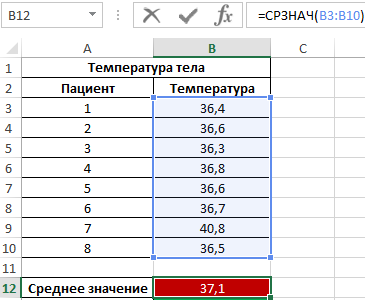
Пример 2. Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.
Формула для нахождения среднего значения:
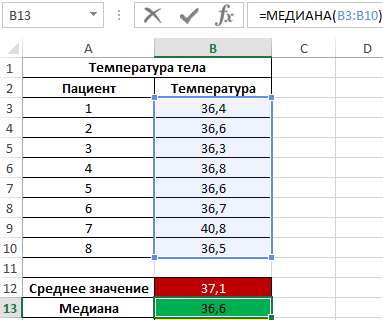
Формула для нахождения медианы:
Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.
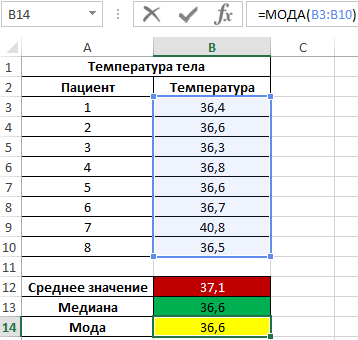
Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:
То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.
Пример расчета медианы при статистическом анализе в Excel
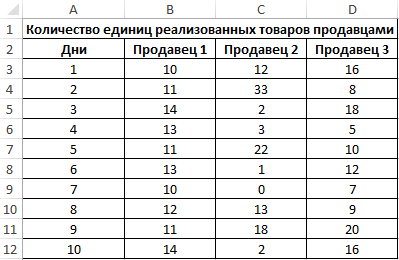
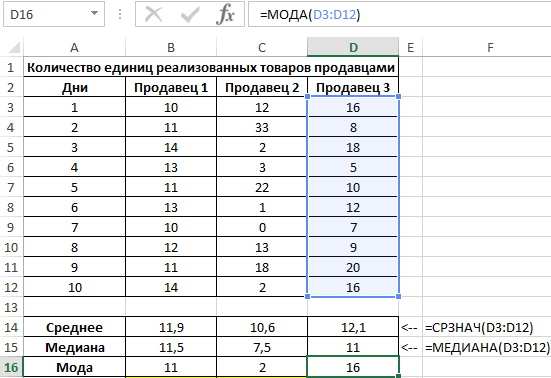
Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.
Исходная таблица данных:
Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:
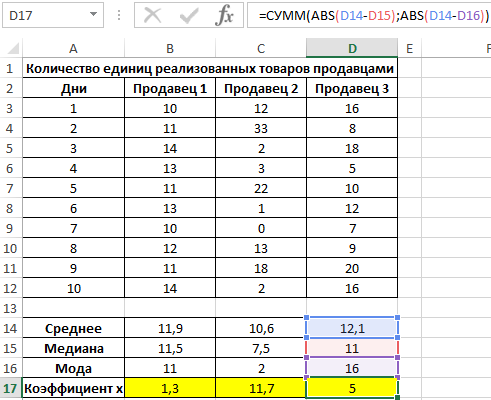
Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:
Рассчитаем значение коэффициента x для первого продавца:
Аналогично проведем расчеты для остальных продавцов. Полученные результаты:
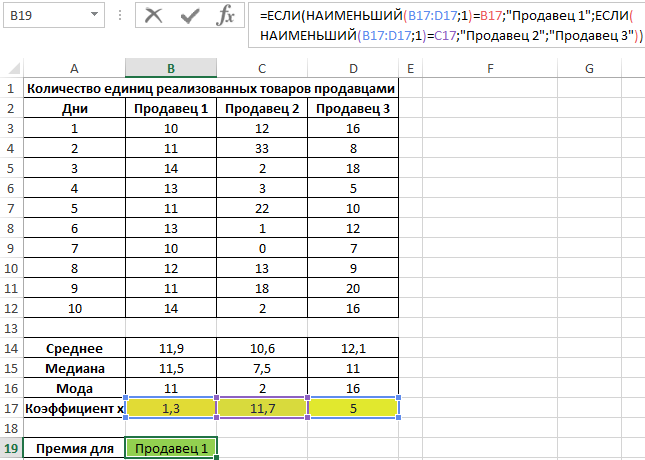
Определим продавца, которому будет выдана премия:
Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.
Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.
Особенности использования функции МЕДИАНА в Excel
Функция имеет следующий синтаксис:
=МЕДИАНА( число1; [число2];. )
Медиана в статистике
Центральную тенденцию данных можно рассматривать не только, как значение с нулевым суммарным отклонением (среднее арифметическое) или максимальную частоту (мода), но и как некоторую отметку (значение в совокупности), делящую ранжированные данные (отсортированные по возрастанию или убыванию) на две равные части. Половина исходных данных меньше этой отметки, а половина – больше. Это и есть медиана.
Итак, медиана в статистике – это уровень показателя, который делит набор данных на две равные половины. Значения в одной половине меньше, а в другой больше медианы. В качестве примера обратимся к набору нормально распределенных случайных чисел.
Очевидно, что при симметричном распределении середина, делящая совокупность пополам, будет находиться в самом центре – там же, где средняя арифметическая (и мода). Это, так сказать, идеальная ситуация, когда мода, медиана и средняя арифметическая совпадают и все их свойства приходятся на одну точку – максимальная частота, деление пополам, нулевая сумма отклонений – все в одном месте. Однако, жизнь не так симметрична, как нормальное распределение.
Допустим, мы имеем дело с техническими замерами отклонений от ожидаемой величины чего-нибудь (содержания элементов, расстояния, уровня, массы и т.д. и т.п.). Если все ОК, то отклонения, скорее всего, будут распределены по закону, близкому к нормальному, примерно, как на рисунке выше. Но если в процессе присутствует важный и неконтролируемый фактор, то могут появиться аномальные значения, которые в значительной мере повлияют на среднюю арифметическую, но при этом почти не затронут медиану.
Медиана выборки – это альтернатива средней арифметической, т.к. она устойчива к аномальным отклонениям (выбросам).
Математическим свойством медианы является то, что сумма абсолютных (по модулю) отклонений от медианного значения дает минимально возможное значение, если сравнивать с отклонениями от любой другой величины. Даже меньше, чем от средней арифметической, о как! Данный факт находит свое применение, например, при решении транспортных задач, когда нужно рассчитать место строительства объектов около дороги таким образом, чтобы суммарная длина рейсов до него из разных мест была минимальной (остановки, заправки, склады и т.д. и т.п.).
Формула медианы
Формула медианы в статистике для дискретных данных чем-то напоминает формулу моды. А именно тем, что формулы как таковой нет. Медианное значение выбирают из имеющихся данных и только, если это невозможно, проводят несложный расчет.
Первым делом данные ранжируют (сортируют по убыванию). Далее есть два варианта. Если количество значений нечетно, то медиана будет соответствовать центральному значению ряда, номер которого можно определить по формуле:
№Me – номер значения, соответствующего медиане,
N – количество значений в совокупности данных.
Тогда медиана обозначается, как
Это первый вариант, когда в данных есть одно центральное значение. Второй вариант наступает тогда, когда количество данных четно, то есть вместо одного есть два центральных значения. Выход прост: берется средняя арифметическая из двух центральных значений:
В интервальных данных выбрать конкретное значение не представляется возможным. Медиану рассчитывают по определенному правилу.
Для начала (после ранжирования данных) находят медианный интервал. Это такой интервал, через который проходит искомое медианное значение. Определяется с помощью накопленной доли ранжированных интервалов. Где накопленная доля впервые перевалила через 50% всех значений, там и медианный интервал.
Не знаю, кто придумал формулу медианы, но исходили явно из того предположения, что распределение данных внутри медианного интервала равномерное (т.е. 30% ширины интервала – это 30% значений, 80% ширины – 80% значений и т.д.). Отсюда, зная количество значений от начала медианного интервала до 50% всех значений совокупности (разница между половиной количества всех значений и накопленной частотой предмедианного интервала), можно найти, какую долю они занимают во всем медианном интервале. Вот эта доля аккурат переносится на ширину медианного интервала, указывая на конкретное значение, именуемое впоследствии медианой.
Обратимся к наглядной схеме.
Немного громоздко получилось, но теперь, надеюсь, все наглядно и понятно. Чтобы при расчете каждый раз не рисовать такой график, можно воспользоваться готовой формулой. Формула медианы имеет следующий вид:
где xMe — нижняя граница медианного интервала;
iMe — ширина медианного интервала;
∑f/2 — количество всех значений, деленное на 2 (два);
S(Me-1)— суммарное количество наблюдений, которое было накоплено до начала медианного интервала, т.е. накопленная частота предмедианного интервала;
fMe — число наблюдений в медианном интервале.
Как нетрудно заметить, формула медианы состоит из двух слагаемых: 1 – значение начала медианного интервала и 2 – та самая часть, которая пропорциональна недостающей накопленной доли до 50%.
Для примера рассчитаем медиану по следующим данным.
Требуется найти медианную цену, то есть ту цену, дешевле и дороже которой по половине количества товаров. Для начала произведем вспомогательные расчеты накопленной частоты, накопленной доли, общего количества товаров.
По последней колонке «Накопленная доля» определяем медианный интервал – 300-400 руб (накопленная доля впервые более 50%). Ширина интервала – 100 руб. Теперь остается подставить данные в приведенную выше формулу и рассчитать медиану.
То есть у одной половины товаров цена ниже, чем 350 руб., у другой половины – выше. Все просто. Средняя арифметическая, рассчитанная по этим же данным, равна 355 руб. Отличие не значительное, но оно есть.
Расчет медианы в Excel
Медиану для числовых данных легко найти, используя функцию Excel, которая так и называется — МЕДИАНА. Другое дело интервальные данные. Соответствующей функции в Excel нет. Поэтому нужно задействовать приведенную выше формулу. Что поделаешь? Но это не очень трагично, так как расчет медианы по интервальным данным – редкий случай. Можно и на калькуляторе разок посчитать.
Напоследок предлагаю задачку. Имеется набор данных. 15, 5, 20, 5, 10. Каково среднее значение? Четыре варианта:
Мода, медиана и среднее значение выборки – это разный способ определить центральную тенденцию в выборке.
Ниже видеоролик о том, как рассчитать медиану в Excel.