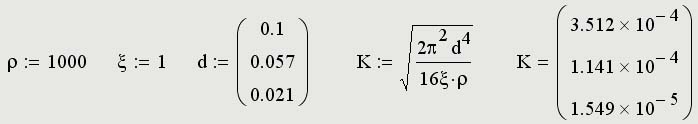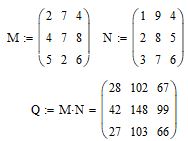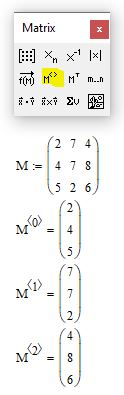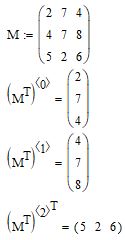Как посчитать матрицу в маткаде
Как посчитать матрицу в маткаде
Векторы и матрицы рассматриваются в программе Mathcad как одномерные и двумерные массивы данных.
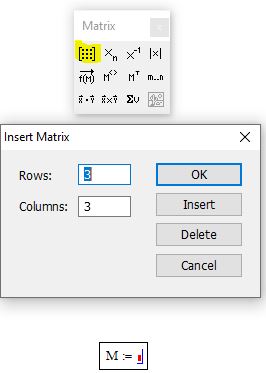
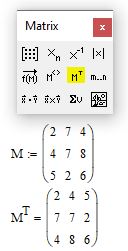
Матрица создается с помощью диалогового окна Вставить матрицу (рис. 1.6), которое открывают командой Вставка > Матрица (Insert > Matrix) или первой кнопкой на панели «Матрица» (рис. 1.7). Вектор задается как матрица, имеющая один столбец. В диалоговом окне задается число строк и столбцов, а после вставки на рабочий лист матрица содержит вместо элементов заполнители, вместо которых следует вставить число, переменную или выражение.
Для матриц определены сложение, умножение на число, перемножение и другие операции. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы:
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля, что задается системной переменной ORIGIN, и может быть изменено пользователем (например, блок ORIGIN:=1 устанавливает начальный индекс равным единице). Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Индекс (Subscript, xn) на панели инструментов Mатрица (Matrix) или нажатием символа «[» после имени массива (см. приложение «Горячие клавиши»). Индексы двумерных матриц записываются через запятую.
Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки: . Для его ввода используется кнопка Столбец (Matrix Column) на панели инструментов Матрица или соответствующая «горячая» клавиша.
На рис. 1.8 приведены примеры реализации некоторых операций с матрицами.
Как посчитать матрицу в маткаде
Совет
Никогда не применяйте для обозначения скалярного произведения символ х,который является общеупотребительным символом векторного произведения (см. разд. 9.1.7).
Рис. 9.3. Оператор векторизации
Листинг 9.16. Использование векторизациидля перемножения элементов вектора
Оператор векторизации можно использовать только с векторами и матрицами одинакового размера.
Большинство неспецифических функций MathCAD не требуют векторизации для проведения одной и той же операции над всеми элементами вектора. Например, аргументом тригонометрических функций по определениюявляется скаляр. Если попытаться вычислить синус векторной величины,MathCAD осуществит векторизацию по умолчанию, вычислив синус каждого элемента и выдав в качестве результата соответствующий вектор. Пример показан в листинге 9.17.
Листинг 9.17. Векторизация необязательнадля большинства функций MathCAD
9.1.12. Символьные операции с матрицами
Все матричные и векторные операторы, о которых шла речь выше, допустимо использовать в символьных вычислениях. Мощь символьных операцийзаключается в возможности проводить их не только над конкретными числами, но и над переменными. Несколько примеров приведены в листинге 9.18.
Листинг 9.18. Примеры символьных операций над векторами и матрицами
Cовет
Смело используйте символьный процессор в качестве мощного математического справочника. Например, когда вы хотите вспомнить какое-либо определение из области линейной алгебры (так, правила перемножения и обращенияматриц показаны в первых строках листинга 9.18).
Примечание
О вложенных массивах читайте в разд. «Создание тензора» гл. 4.
Пример использования функции CreateSpace показан на рис. 9.4. Заметьте, дляпостроения графика спирали не потребовалось никакого дополнительногокода, кроме определения параметрической зависимости в вектор-функции F!
Примечание
Размер NXM матрицы А для функции geninv должен быть таким, чтобы N>M.
Примечание
Выделить из матрицы один столбец или строку можно и с помощью функции submatrix.
Примечание
Число элементов вектора и индекс его последнего элемента совпадают, еслииндексы нумеруются с 1, т. е. системная константа ORIGIN равна 1 (см. гл. 4).
Примечание
Если элементы матриц или векторов комплексные, то сортировка ведется подействительной части, а мнимая часть игнорируется.
Совет
В большинстве задач неважно, какую норму использовать. Как видно, в обычных случаях разные нормы дают примерно одинаковые значения, хорошо отражая порядок величины матричных элементов. Определение остальных нормзаинтересованный читатель отыщет в справочниках по линейной алгебре илив Центре Ресурсов MathCAD.
Примечание
Как нетрудно понять, матрицы А и в из предыдущего листинга 9.30 обладаютодинаковыми числами обусловленности, т.к. в=100-А, и, следовательно, обематрицы определяют одну и ту же систему уравнений.
Примечание
К системам линейных уравнений сводится множество, если не сказать большинство, задач вычислительной математики. Один из таких примеров приведен в разд. «Разностные схемы»гл. 12.
Примечание
Соответствующая матрице А и вектору B система уравнений выписана явнов листинге 9.35.
Листинг 9.33. Решение СЛАУ
Листинг 9.34. Символьное решение СЛАУ (продолжение листинга 9.33)
В некоторых случаях, для большей наглядности представления СЛАУ, егоможно решить точно так же, как систему нелинейных уравнений (см. гл. 8). Пример численного решения СЛАУ из предыдущих листингов показан влистинге 9.35. Не забывайте, что при численном решении всем неизвестнымтребуется присвоить начальные значения (это сделано в первой строке листинга 9.35). Они могут быть произвольными, т. к. решение СЛАУ с невырожденной матрицей единственно.
Примечание
Фактически, треугольное разложение матрицы системы линейных уравненийпроизводится при ее решении численным методом Гаусса.
Работа с матрицами в MathCad 15
В статье рассмотрены основные возможности mathcad 15 для работы с матрицами
Ввод матрицы
Чтобы ввести матрицу в mathcad 15 нужно в свободном поле ввести с клавиатуры имя матрицы. Пусть это будет M. Затем на панели Matrix нужно нажать кнопку «Matrix or vector». В появившемся окне нужно ввести количество строк и столбцов и нажать OK
Рис. 1. Ввод матрицы
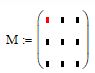
Затем появится заготовка матрицы с пустыми маркерами для ввода элементов вручную. См. рис. 2
Рис. 2. Заполнение матрицы
Перемножение матриц
Как известно, перемножение матриц осуществляется по правилу «строка на столбец». Введем 2 матрицы 3 х 3 с именами M и N. Перемножение матриц осуществляется с помощью стандартной операции умножения. На рис. 3 смотрите синтаксис записи
Рис. 3. Перемножение матриц
Транспонирование матриц
Как известно, при транспонировании матрицы ее строки становятся столбцами. В mathcad есть функция, которая позволяет выполнить транспонирование. Введите имя матрицы, которую хотите транспонировать, и на панели Matrix нажмите кнопку «Matrix transpose». На рис. 4 смотрите синтаксис для записи этой операции.
Рис. 4. Транспонирование матрицы
Обратные матрицы
Как известно, обратной матрицей M^-1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку «Invers». на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы
Рис. 5. Обратная матрица
Выделение столбца и строки из матрицы
Для того чтобы «вытащить» столбец из матрицы можно воспользоваться стандартной функцией mathcad из панели matrix. Введите произвольную матрицу M и затем ниже в рабочем поле mathcad выполните операцию, как показано на рис. 6. Обратите внимание, что по умолчанию номера столбцов и строк индексируются с «нуля»
Рис. 6. Выделение столбца матрицы
Аналогичным способом можно выделить строку, но для этого матрицу предварительно нужно транспонировать. При этом строка будет отображена в виде столбца. Если вы хотите получить результат в виде строки, то операцию транспонирования нужно провести 2 раза. Синтаксис будет выглядеть как на рисунке 7
Рис. 7. Выделение строки матрицы
Обратите внимание, что если при перемножении матриц их размерность «не совпадает» то mathcad выдаст ошибку
Обратите внимание, что обратная матрица не всегда может существовать для исходной матрицы
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Работа с матрицами в MathCAD
Практическая работа № 3
В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами.
Предварительно матрицу нужно определить и ввести в рабочий документ MathCAD.
Для того чтобы определить матрицу, введите с клавиатуры имя матрицы и знак присваивания ( + ). Затем откройте панель операций с матрицами и нажмите кнопку «Создать матрицу или вектор» или выберите в меню Вставка (Insert) команду Матрицу (Matix). В окне диалога введите число строк и столбцов и заполните значениями поле ввода матрицы.
Большинство вычислений с матрицами, как и другие вычисления в MathCAD, можно выполнять тремя способами – с помощью панелей инструментов, выбором операции в меню или обращением к соответствующей функции.
За кнопками на панели инструментов Матрицы закреплены следующие функции:
· определение размеров матрицы
· Xn – ввод нижнего индекса
· поэлементные операции с матрицами: если 
· M T – транспонирование матрицы:
· 
· 
· 

· 
· визуализация цифровой информации, сохраненной в матрице.
Для того, чтобы выполнить какую-либо операцию с помощью панели инструментов, нужно выделить матрицу и щелкнуть в панели по кнопке операции либо щелкнуть по кнопке в панели и ввести в помеченной позиции имя матрицы.
Функции, предназначенные для решения задач линейной алгебры, собраны в разделе Векторы и матрицы (Vector and Matrix); их можно разделить на три группы: функции определения матриц и операции с блоками матриц, функции вычисления различных числовых характеристик матриц и функции, реализующие численные алгоритмы решения задач линейной алгебры.
Функции определения матриц и операции с блоками матриц:
· matrix(m, n, f) – создает и заполняет матрицу размерности m x n, элемент которой, расположенный в i-ой строке, j-ом столбце, равен значению f(i,j) функции f(x,y);
· diag(v) – создает диагональную матрицу, элементы главной диагонали хранятся в векторе v;
· identity(n) – создает единичную матрицу порядка n;
· augment(A, B) – формирует матрицу, в первых столбцах которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число строк);
· stack(A, B) – формирует матрицу, в первых строках которой содержится матрица A, а в последних – матрица B (матрицы A и B должны иметь одинаковое число столбцов);
· submatrix(A, ir, jr, ic, jc) – формирует матрицу, которая является блоком матрицы A, расположенным в строках с ir по jr и в столбцах с ic по jc (ir
· eigenvec(A, l) – вычисление собственного вектора матрицы A, отвечающего собственному значению l;
· lsolve(A, b) – решение системы линейных алгебраических уравнений Ax=b.
Вычисления с использованием описанных функций выполняются стандартным для MathCAD способом. Чтобы обратиться к функции, введите с клавиатуры имя функции, перечислите в скобках ее аргументы, введите знак равенства и щелкните по свободному месту в рабочем документе вне выделяющей рамки. Результат вычислений (число, вектор, матрица) будет отображен в рабочем документе справа от знака равенства.
Если предполагается использовать результаты в дальнейших вычислениях, им следует присвоить имя. Для этого введите с клавиатуры имя переменной и знак присваивания, а справа от него – имя функции со списком аргументов в круглых скобках. Если теперь ввести с клавиатуры имя переменной, знак равенства и щелкнуть по свободному месту в рабочем документе вне выделяющей рамки, то результат вычислений будет отображен справа от знака равенства.
Имя функции можно вставить из списка: щелкните по месту вставки, затем по строке Функция (Function)меню Вставка (Insert), выберите в окне списка стрелками прокрутки нужную функцию и подтвердите выбор щелчком по кнопке OK в окне диалога.
Вычисления могут производиться в двух режимах – автоматическом и последовательном. В первом случае операция выполняется сразу после ввода команды и щелчка по рабочему документу вне выделяющей рамки, во втором – после команды Вычислить (Calculate). Режим вычислений устанавливается в меню Математика (Math). По умолчанию включен режим автоматических вычислений.
MathCAD читает и выполняет введенные выражения слева направо и сверху вниз, поэтому следите, чтобы выражение для вычисления располагалось правее и ниже определенных для него значений переменных.
Задание
1. Создать матрицу А заданной размерности n*m (матрицу заполнить самостоятельно).
2. Транспонировать матрицу А.
3. Вычленить из матрицы А i-ый и j-ый столбцы и найти их сумму и скалярное произведение.
4. Применить к каждому элементу матрицы А функцию z(x).
Указания
1. В начале работы переменной ORIGIN присвоить значение 1. Для выполнения операций над матрицей пользоваться панелью инструментов Матрицы, для вставки функций пользоваться меню Вставка – Функция или соответствующей кнопкой панели инструментов Стандартная.
2. Для выполнения 4 задания необходимо:
· Записать функцию z(x) в общем виде.
· Переменным i и j присвоить диапазоны значений: 
· Вычислить элементы новой матрицы Z как значения функции z(x), где в качестве переменной x подставляется элемент матрицы A: 
· Просмотреть полученную матрицу Z (набрать с клавиатуры Z=).
3. Для записи функции, заданной с условиями необходимо:
· Записать диапазон изменения аргументов x и y: 
· Записать «f(x,y):=», затем на панели инструментов «Программирование» нажать кнопку «Add line». В поле ввода функции появится вертикальная черта с метками для ввода.
· В верхней метке набрать первое значение функции, а затем нажать кнопку «if», появится служебное слово if и метка для ввода условия. Для применения логической операции «И» для нескольких логических выражений ставится знак «*», а для операции «ИЛИ» – знак «+».
· В нижней метке набрать второе значение функции и нажать кнопку «otherwise» (иначе). Щелкнуть за пределами поля ввода функции для завершения записи.
4. Для исследования однородной системы уравнений необходимо вычислить определитель матрицы коэффициентов. Если определитель не равен 0, то система нетривиально совместна и имеет более одного решения (в том числе нулевые). Справедливо также утверждение: для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных n. Таким образом, если |C|≠0 и rank(C)≤n, то система тривиально совместна и имеет только одно нулевое решение.
Варианты заданий.
Размерность матрицы А 3*4.

Размерность матрицы А 5*3.

Размерность матрицы А 4*4.

Размерность матрицы А 7*4.

Размерность матрицы А 7*8.

Размерность матрицы А 7*7.

Размерность матрицы А 7*8.

Размерность матрицы А 7*5.

Размерность матрицы А 5*7.

Размерность матрицы А 5*4.

Размерность матрицы А 7*7.

Размерность матрицы А 4*5.

Размерность матрицы А 6*7.

Размерность матрицы А 6*4.

Размерность матрицы А 7*6.

Размерность матрицы А 6*5.
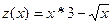
Размерность матрицы А 9*5.

Размерность матрицы А 7*6.

Размерность матрицы А 7*4.

Размерность матрицы А 8*4.

Размерность матрицы А 5*7.

Размерность матрицы А 5*5.
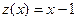
Размерность матрицы А 5*4.
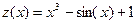
Размерность матрицы А 4*5.

Размерность матрицы А 3*7.

Размерность матрицы А 5*4.