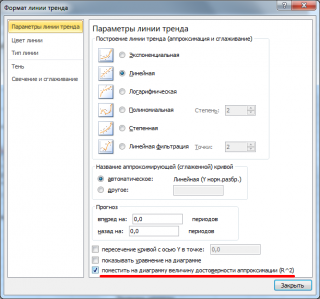
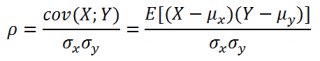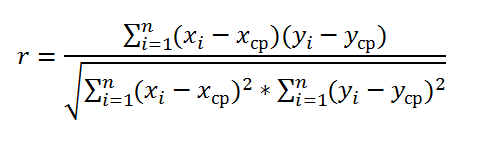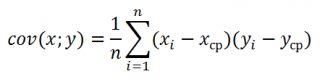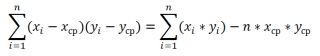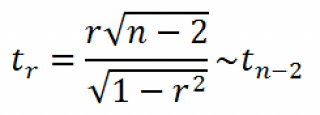Как посчитать корреляцию в экселе
Коэффициент корреляции: использование, формулы и пример расчёта в Excel
Приветствую всех читателей моего блога! Думаю вы наверняка замечали, что некоторые явления связаны между собой. Например, температура воздуха на улице и количество прогуливающихся людей, время суток и количество друзей онлайн в соцсети, благосостояние страны и количество нобелевских лауреатов (хотя тут все же спорно). Одни явления связаны сильнее, другие слабее и сила этой связи называется корреляцией. Ее измерение имеет непосредственное отношение к портфельному инвестированию и диверсификации инвестиционных активов.
Например, проанализировав данные по ВВП на душу населения и продолжительности жизни в странах мира, мы невооруженным глазом заметим тенденцию:
А благодаря расчёту коэффициента корреляции мы можем узнать силу взаимосвязи в конкретном числовом выражении. Это очень удобно и полезно при анализе данных в самых разных областях науки, в том числе в экономике и инвестировании.
Сегодня я расскажу вам подробнее о том, что такое корреляция простыми словами, без сложных формул и терминов. Также я покажу вам, как правильно и легко рассчитать коэффициент корреляции в Excel и как правильно интерпретировать результаты, чтобы использовать их для составления инвестиционного портфеля.
Спасибо за внимание, продолжаем!
Что такое корреляция простыми словами
Не хочу вас сразу грузить формулами и расчётами, об этом поговорим ближе к концу. Давайте сначала разберемся, что по своей сути означает цифра коэффициента корреляции, которую вы можете встретить в какой-нибудь книге или статье.
Если значение близко к единице или минус единице — значит два явления так или иначе сильно взаимосвязаны. Впрочем, причины этого не всегда очевидны — явление А может влиять на явление B, может быть наоборот. Нередко бывает, что существует явление C, которое приводит в движение А и В одновременно. В общем, природа корреляции — это уже второй вопрос, которым должны заниматься исследователи.
При высокой положительной корреляции вслед за графиком А растёт и график B, и чем выше значение, тем слаженнее оба движутся. Для наглядности, вот как выглядит корреляция +1:
Движения графиков полностью повторяют друг друга, причем это как в случае простого добавления, так и с множителем.
Движения графиков похожи на зеркальные отражения.
Коэффициент корреляции — удобный инструмент для анализа во многих сферах науки и жизни. Его легко рассчитать в Excel и применить, поэтому самая большая сложность в работе с ним — грамотно подобрать данные для расчёта. Основное правило — чем больше данных, тем лучше. Многие взаимосвязи проявляют себя лишь на длинной дистанции.
Также нужно следить за тем, чтобы найденные корреляции не были ложными.
Ложные корреляции
Дело в том, что с помощью коэффициента корреляции можно проверить на взаимосвязь любые явления, которые можно выразить в числовом выражении. То есть, реально любые — например количество свадеб в Нью-Йорке и объем импорта нефти в США из Норвегии:
Корреляция составила 86%! Действительно ли свадьбы влияют на экспорт нефти? Разумеется, нет — подобная зависимость совершенно случайна. Именно так выглядит ловушка ложной корреляции — она может показать взаимосвязь там, где её на самом деле нет.
Не хочу сильно заострять внимание на этой проблеме, так что если интересно поразбираться — нашел для вас видео, в котором найдете еще несколько примеров странных взаимосвязей и причины их появления:
В общем, на результаты корреляционного анализа есть смысл обращать внимание, когда связь между явлениями уже известна или подозревается. В противном случае это может быть всего лишь число, которое ничего не значит.
Корреляция и диверсификация
Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации, которая неразрывно связана с понятием корреляции. Это улавливается даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.
Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:
Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:
Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.
А вот пример портфеля двух активов с корреляцией близкой к 0:
Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:
Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.
Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:
Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.
Коэффициент корреляции и ПАММ-счета
С расчётом корреляции я как студент экономического ВУЗа познакомился еще на втором курсе. Тем не менее, долгое время недооценивал важность расчёта корреляции именно для подбора ПАММ-портфеля. 2018 год очень четко показал, что ПАММ-счета с похожими стратегиями в случае кризиса могут вести себя очень похоже.
Случилось так, что с середины года отказала не просто одна стратегия управляющего, а большинство торговых систем, завязанных на активные движения валютной пары EUR/USD:
Рынок был для каждого управляющего по-своему неблагоприятным, но присутствие их всех в портфеле привело к большой просадке. Совпадение? Не совсем, ведь это были ПАММ-счета с похожими элементами в торговых стратегиях. Без опыта торговли на рынке Форекс может быть сложно понять, как это работает, но по корреляционной таблице степень взаимосвязи видна и так:
Мы ранее рассматривали корреляцию вплоть до +1, но как видите на практике даже совпадение в районе 20-30% уже говорит о некоторой схожести ПАММ-счетов и, как следствие, результатов торговли.
Чтобы снизить шансы на повторение ситуации, как в 2018 году, я считаю в портфель стоит подбирать ПАММ-счета с низкой взаимной корреляцией. По сути, нам нужны уникальные стратегии с разными подходами и разными валютными парами для торговли. На практике, конечно, сложнее подобрать прибыльные счета с уникальными стратегиями, но если хорошо покопаться в рейтинге ПАММ-счетов, то все возможно. К тому же, низкая взаимная корреляция снижает требования для диверсификации, 5-6 счетов вполне хватит.
Пару слов о расчёте коэффициента корреляции для ПАММ-счетов. Достать сами данные относительно несложно, в Альпари прямо с сайта, для остальных площадок через сайт investflow.ru. Однако с ними нужно сделать небольшие преобразования.
Данные о прибыльности ПАММов изначально хранятся в формате накопленной доходности, нам это не подходит. Корреляция стандартных графиков доходности двух прибыльных ПАММ-счетов всегда будет очень высокой, просто потому что они все движутся в правый верхний угол:
У всех счетов положительная корреляция от 0.5 и выше за редким исключением, так мы ничего не поймем. Реальное сходство стратегий ПАММ-счетов можно увидеть только по дневным доходностям. Рассчитать их не особо сложно, если знаете нужные формулы доходности. Если прибыль или убыток двух ПАММ-счетов совпадают по дням и по процентам, высока вероятность что их стратегии имеют общие элементы — и коэффициент корреляции нам это покажет:
Как видите, некоторые корреляции стали нулевыми, а некоторые остались на высоком уровне. Мы теперь видим, какие ПАММ-счета действительно похожи между собой, а какие не имеют ничего общего.
Напоследок давайте разберёмся, что делать и как посчитать корреляцию, если у вас появилась в этом необходимость.
Коэффициент корреляции в Excel и формула расчёта
Вероятно, вас интересует, как самостоятельно рассчитать корреляцию двух инвестиционных активов. До изобретения компьютеров приходилось делать это вручную, для чего использовалась вот такая формула коэффициента корреляции:
Кстати, студентам на экзамене до сих пор компьютеров не выдают, хоть калькулятор можно и на том спасибо. Как вы понимаете, занятие все равно трудоёмкое 🙂
Профессиональному инвестору может понадобиться рассчитать сотни корреляций, так что вариант по формуле не подходит. Естественно, эта задача уже давно автоматизирована, и, как по мне, проще всего рассчитать коэффициент корреляции в Excel.
Чтобы далеко за примером не ходить, давайте рассчитаем корреляцию двух популярных ПАММ-счетов Lucky Pound и Hohla EUR. Они находятся на площадке компании Alpari, а значит мы можем скачать историю доходности прямо с сайта:
Далее нам надо скопировать историю доходности в один файл, для удобства. Для точного расчета корреляции в Excel нам в принципе хватит и двух лет истории, располагаем данные так:
Теперь, как я уже писал выше, для ПАММ-счетов (и для многих других инвестиционных инструментов) надо рассчитать дневные доходности:
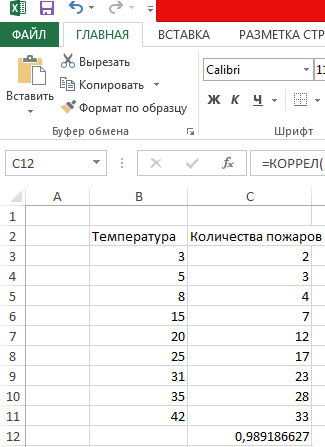
А дальше все просто — используется встроенная формула коэффицента корреляции в Excel =КОРРЕЛ():
Получили значение 0.12, а значит стратегии ПАММ-счетов практически не имеют ничего общего. Это хорошо для диверсификации, так что можно добавлять обоих в инвестиционный портфель.
При желании, можно сделать табличку на весь ваш портфель. Тогда если у вас появится новый вариант для инвестирования, вы сможете сразу сравнить его с каждым активом и увидеть, есть ли нежелательные корреляции.
Мне понравилось работать над этой темой и статья получилась неплохой. Есть еще одна интересная тема по основам инвестирования, которую я хочу подробно обсудить… Будет обидно, если пропустите, так что подписывайтесь на обновления блога по почте или через соцсети.
Пример выполнения корреляционного анализа в Excel
Одним из самых распространенных методов, применяемых в статистике для изучения данных, является корреляционный анализ, с помощью которого можно определить влияние одной величины на другую. Давайте разберемся, каким образом данный анализ можно выполнить в Экселе.
Назначение корреляционного анализа
Сила зависимости определяется по модулю коэффициента корреляции. Чем больше значение, тем сильнее изменение одной величины влияет на другую. Исходя из этого, при нулевом коэффициенте можно утверждать, что взаимосвязь отсутствует.
Выполняем корреляционный анализ
Для изучения и лучшего понимания корреляционного анализа, давайте попробуем его выполнить для таблицы ниже.
Здесь указаны данные по среднесуточной температуре и средней влажности по месяцам года. Наша задача – выяснить, существует ли связь между этими параметрами и, если да, то насколько сильная.
Метод 1: применяем функцию КОРРЕЛ
В Excel предусмотрена специальная функция, позволяющая сделать корреляционный анализ – КОРРЕЛ. Ее синтаксис выглядит следующим образом:
Порядок действий при работе с данным инструментом следующий:
Метод 2: используем “Пакет анализа”
Альтернативным способом выполнения корреляционного анализа является использование “Пакета анализа”, который предварительно нужно включить. Для этого:
Все готово, “Пакет анализа” активирован. Теперь можно перейти к выполнению нашей основной задачи:
Заключение
Таким образом, выполнение корреляционного анализа в Excel – достаточно автоматизированная и простая в освоении процедура. Все что нужно знать – где найти и как настроить необходимый инструмент, а в случае с “Пакетом решения”, как его активировать, если до этого он уже не был включен в параметрах программы.
Корреляция и ковариация в EXCEL
history 25 ноября 2018 г.
Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.
Коэффициент корреляции ( критерий корреляции Пирсона, англ. Pearson Product Moment correlation coefficient) определяет степень линейной взаимосвязи между случайными величинами.
Как следует из определения, для вычисления коэффициента корреляции требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки коэффициента корреляции используется выборочный коэффициент корреляции r ( еще он обозначается как R xy или r xy ) :
Теоретическое отступление
Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о корреляции температуры и года наблюдения и, соответственно, применять показатели корреляции с соответствующей их интерпретацией.
Корреляционная связь между переменными может возникнуть несколькими путями:
Таким образом, показатель корреляции показывает, насколько сильна линейная взаимосвязь между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.
Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:
Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:
Использование MS EXCEL для расчета корреляции
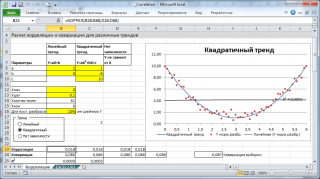
Примечание : В файле примера можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.
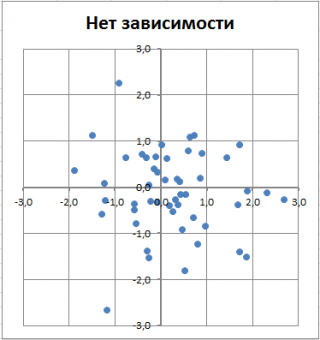
В файле примера для построения диаграммы рассеяния в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.
Примечание : Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.
Для того, чтобы удостовериться, что вычисления корреляции производятся функцией КОРРЕЛ() по вышеуказанным формулам, в файле примера приведено вычисление корреляции с помощью более подробных формул:
Использование MS EXCEL для расчета ковариации
Примечание : Функции КОРРЕЛ() и КОВАР() в английской версии представлены как CORREL и COVAR. Функции КОВАРИАЦИЯ.Г() и КОВАРИАЦИЯ.В() как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета ковариации :
Эти формулы используют свойство ковариации :
Если переменные x и y независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А дисперсия их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
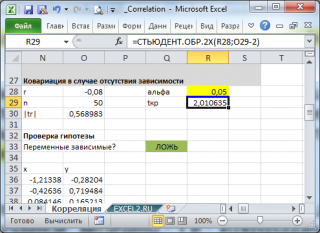
Оценка статистической значимости коэффициента корреляции
Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е. коэффициента корреляции r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t r :
которая имеет распределение Стьюдента с n-2 степенями свободы.
Если вычисленное значение случайной величины |t r | больше, чем критическое значение t α,n-2 (α- заданный уровень значимости ), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).
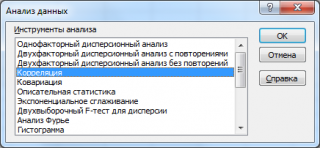
Надстройка Пакет анализа
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).
Как построить график корреляции в Excel
Excel – это эффективный инструмент для статистической обработки данных. И определение корреляций является очень важной составляющей этого процесса. Программа имеет весь необходимый инструментарий для осуществления расчетов такого плана. Сегодня мы более детально разберемся, что нам нужно для осуществления анализа этого типа.
Что представляет собой корреляционный анализ
Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.
Для определения зависимости используется другой тип анализа, который называется регрессионным.
Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:
Ну и наконец, еще один пример ложной корреляции – чем больше сыра люди едят, тем больше людей умирает из-за того, что они запутываются в своих простынях.
Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.
Корреляционный анализ в Excel — 2 способа
Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.
Как рассчитать коэффициент корреляции
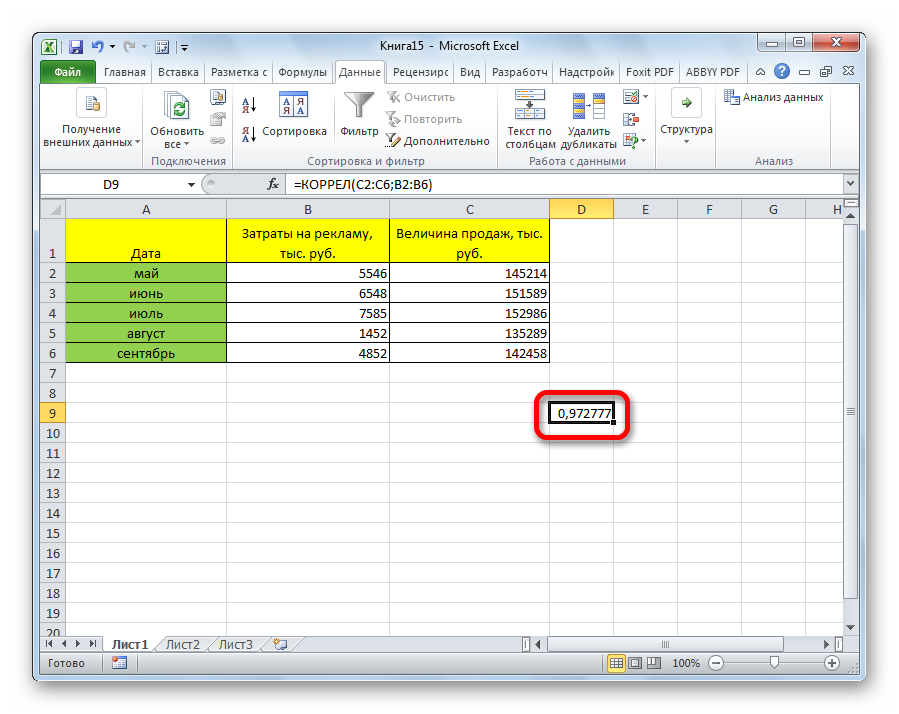
Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.
Способ 1. Определение корреляции с помощью Мастера Функций
Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:
После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов.
Способ 2. Вычисление корреляции с помощью пакета анализа
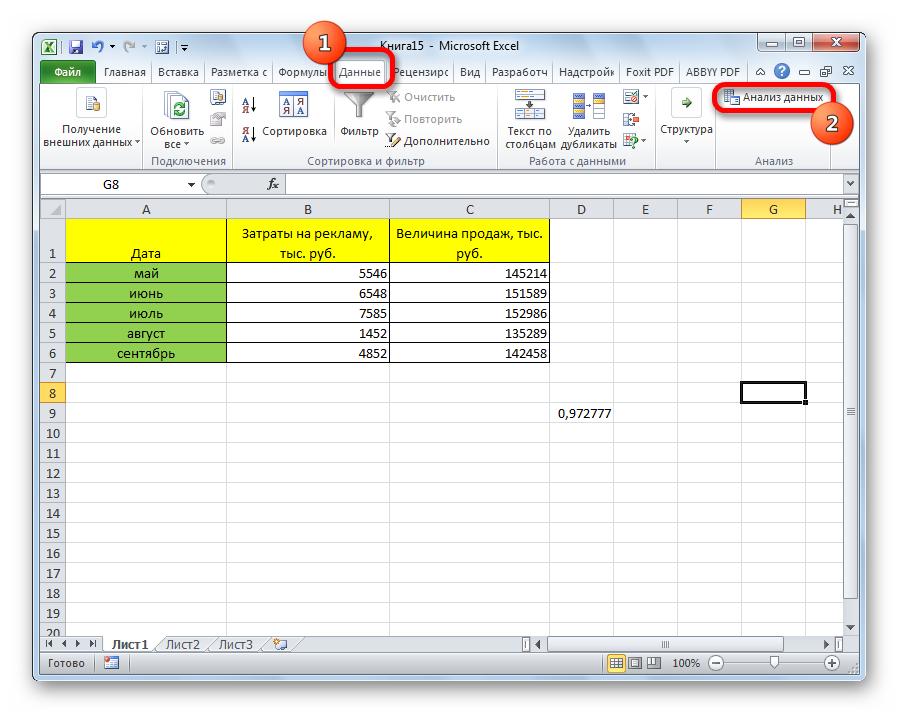
Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:
Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее.
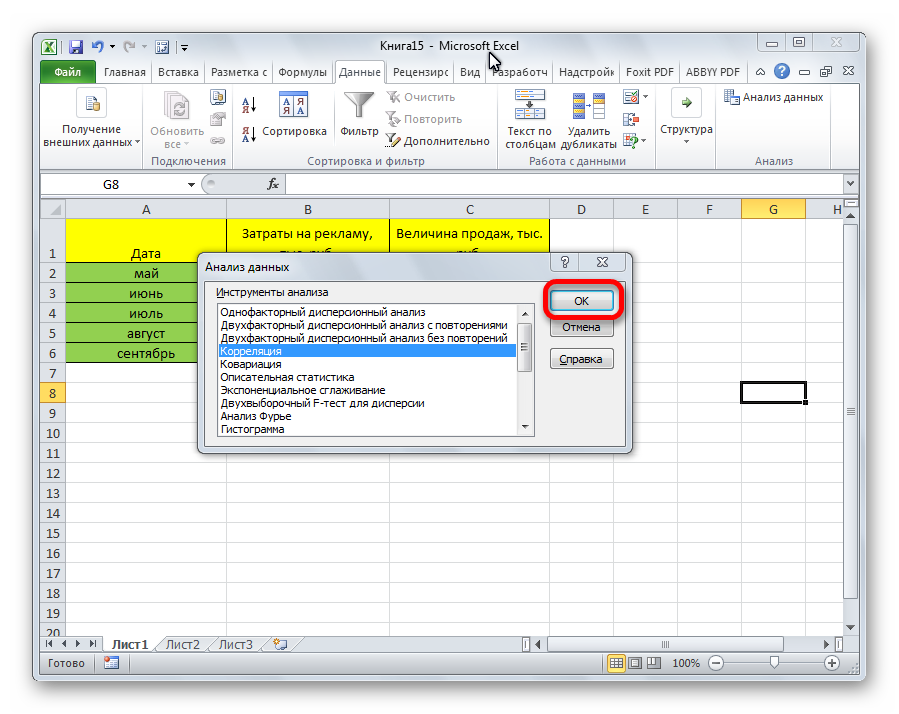
Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК».
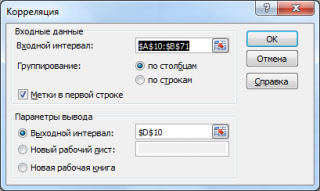
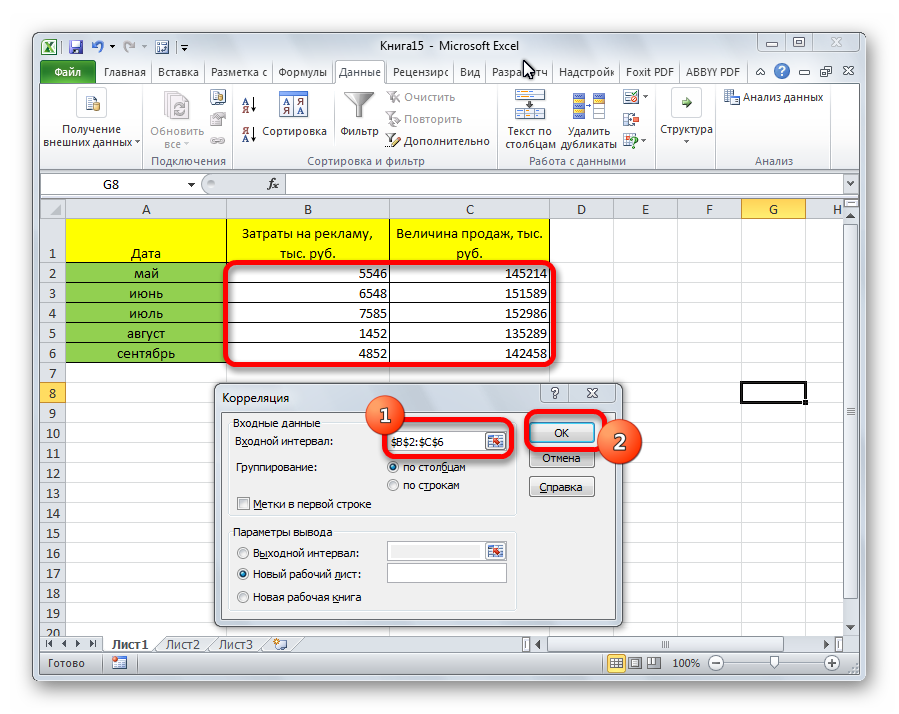
Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».
Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».
В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».
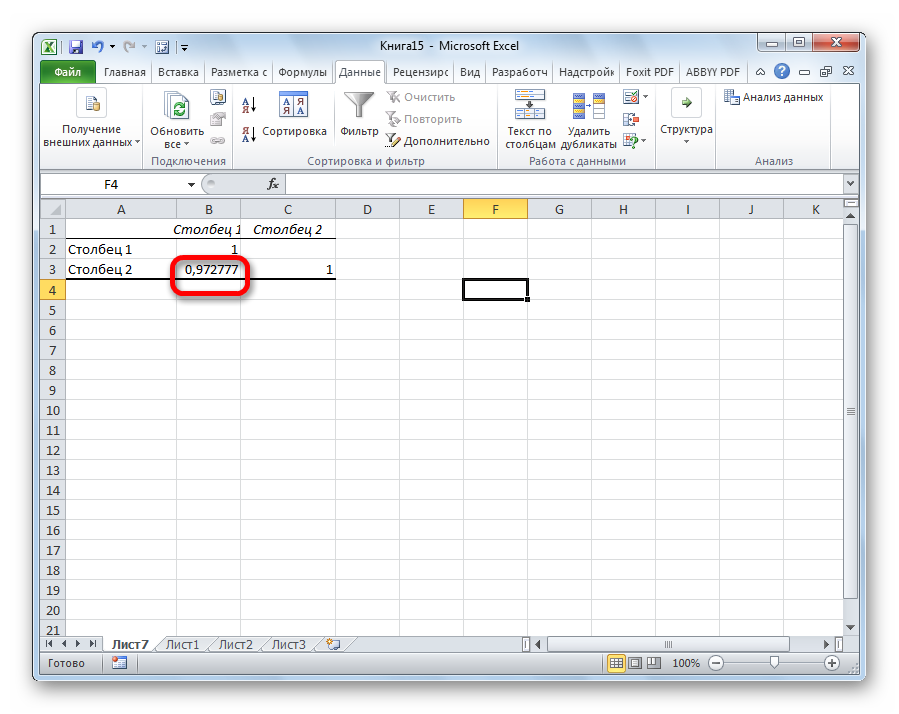
Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более.
Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.
Как построить поле корреляции в Excel
Итак, давайте теперь разберемся, как построить поле корреляции. Для начала нужно разобраться, что это вообще такое. Под корреляционным полем подразумевается фактически график корреляции. Главное требование к такой диаграмме – каждая точка должна соответствовать единице совокупности. Поле корреляции поможет установить более глубокие связи и проанализировать данные более качественно. Для начала нам нужно найти коэффициент корреляции между двумя диапазонами, используя функцию КОРРЕЛ.
После того, как мы это сделали, мы теперь можем сделать поле корреляции. Для этого выполняем следующие действия:
Этот график можно построить не только на основе корреляции, определенной через функцию КОРРЕЛ.
Диаграмма рассеивания. Поле корреляции
До сих пор часть пользователей сидит на старой версии Word. Как построить корреляционное поле в этом случае? Для этого существует специальный инструмент, который называется мастером диаграмм. Найти его можно на панели инструментов по специфическому изображению диаграммы. Если навести на эту иконку мышкой, то появится всплывающая подсказка, которая поможет нам убедиться в том, что это действительно мастер диаграмм.
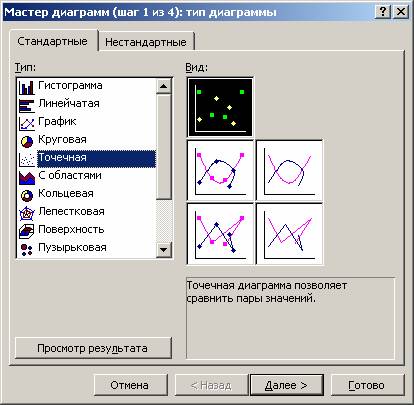
После этого появится диалоговое окно, в котором нам надо выбрать точечный тип диаграммы. Видим, что логика действий в старых версиях офисного пакета в целом остается той же самой, просто немного другой интерфейс. Немного правее мы можем увидеть, как будет выглядеть точечная диаграмма и выбрать подходящий вид, а также прочитать описание этого типа диаграммы. После этого нажимаем на кнопку «Далее».
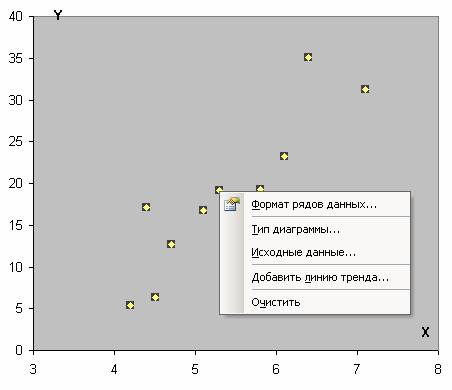
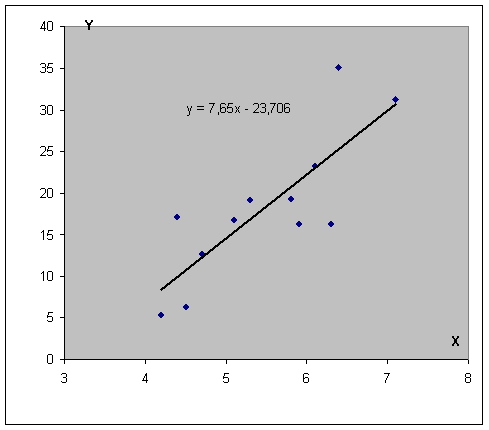
Затем выбираем диапазон данных, и наша линия появляется. После этого можно добавить линию регрессии к графику. Для этого необходимо сделать клик правой кнопкой мыши по одной из точек и в появившемся перечне найти «Добавить линию тренда» и сделать клик по этому пункту.
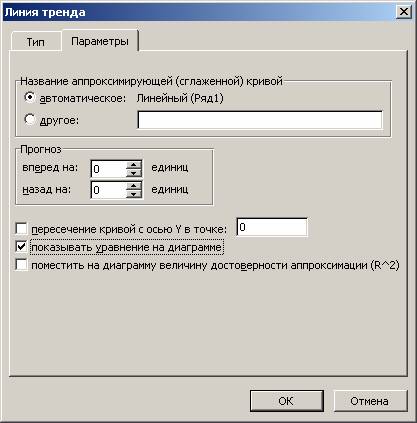
Далее выставляем настройки. Нас интересует тип «Линейная», а в окне параметров нужно поставить флажок «Показывать уравнение на диаграмме».
После подтверждения действий у нас появится что-то типа такого графика.
Как видим, возможных вариантов построения может быть огромное количество.