Как посчитать корень в питоне

Python sqrt (): практическое руководство

Если вы не гений математики, вы не запомните все квадратные корни. И даже если вы это сделали, кто-то другой, глядя на ваш код, может не знать, что вы. Это означает, что им, возможно, придётся перепроверить, что вы написали правильные квадратные корни — это просто переделка работы.

Если вы использовали функцию квадратного корня Python, ясно, что вычисляется квадратный корень. Другой человек, смотрящий на ваш код, знает, что он точен. В качестве дополнительного бонуса никто не должен открывать свой калькулятор!

Что такое Python sqrt ()?

Независимо от того, используете ли вы теорему Пифагора или работаете над квадратным уравнением, функция квадратного корня Python — sqrt () — может помочь вам решить ваши проблемы. Как вы уже догадались, sqrt()вернёт квадрат числа, переданного вами в качестве параметра.

sqrt()Метод может быть полезен, потому что это быстро и точно. В этом кратком руководстве рассматривается, что вы можете передать в качестве параметра sqrt(), способы обхода недопустимых параметров и пример, который поможет вам понять. Вы можете получить квадратный корень из числа, возведя его в степень 0,5 с помощью оператора экспоненты Python (**) или pow()функции.

Когда вы работаете с несколькими числами, требующими квадратного корня, вы обнаружите, что использование sqrt()функции более элегантно, чем использование нескольких операторов экспоненты с «0,5». Кроме того, это более понятно. Можно легко забыть или пропустить лишнюю звёздочку (’*’), которая полностью превратит оператор в оператор умножения, что даст вам совершенно другой результат.

Синтаксис функции квадратного корня Python

Общий синтаксис, используемый для вызова sqrt()функции:

В приведённом выше фрагменте кода «x» — это число, квадратный корень которого вы хотите вычислить. Число, которое вы передаёте в качестве параметра функции извлечения квадратного корня, может быть больше или равно 0. Обратите внимание, что вы можете передать только одно число.

Но к чему относится «математическая» часть синтаксиса выше? Математический модуль — это библиотека Python, которая содержит множество полезных математических функций, одна из которых является sqrt()функцией. Для использования sqrt()вам нужно будет импортировать математический модуль, поскольку именно там хранится код для выполнения функции. Приставляя «math» к префиксу sqrt(), компилятор знает, что вы используете функцию sqrt(), принадлежащую библиотеке «math».

Способ импорта математического модуля состоит в том, чтобы написать ключевое слово «импорт» вместе с именем модуля — в данном случае «математика». Оператор импорта — это простая строка, которую вы пишете перед кодом, содержащим sqrt()функцию:

Результатом функции извлечения квадратного корня является число с плавающей запятой (float). Например, результатом использования sqrt()81 будет 9,0, что является числом с плавающей запятой.

Включите математический оператор импорта в начало любого сеанса файла или терминала / консоли, который содержит код, который использует sqrt().

Как использовать метод Python sqrt ()

Вы можете передавать положительные числа типа с плавающей запятой или целочисленного типа int. В предыдущем примере мы видели int 81 в качестве параметра. Но мы также можем передать число с плавающей запятой, 70,5, например:

Результат этого расчёта: 8,916277250063503. Как видите, результат довольно точный. Теперь вы можете понять, почему имеет смысл, что результат всегда будет двойным, даже если квадратный корень из числа такой же простой, как «9».

Вы также можете передать переменную, представляющую число:

yourValue= 90
math.sqrt(yourValue)
# 9.486832980505138

И вы также можете сохранить результат в переменной:

Сохранение этого в переменной упростит вывод на экран:

Работа с отрицательными числами с помощью abs ()

Квадратный корень из любого числа не может быть отрицательным. Это потому, что квадрат является произведением самого числа, и если вы умножите два отрицательных числа, отрицательные числа уравняются, и результат всегда будет положительным. Если вы попытаетесь передать отрицательное число sqrt(), вы получите сообщение об ошибке, и ваш расчёт не будет выполнен.

abs()Функция возвращает абсолютное значение заданного числа. Абсолютное значение −9 будет 9. Аналогично, абсолютное значение 9 равно 9. Поскольку sqrt()оно предназначено для работы с положительными числами, отрицательное число вызовет исключение ValueError.

Предположим, вы передаёте переменные sqrt()и не можете узнать, все ли они положительны, не просматривая длинные строки кода, чтобы найти значения переменных. В то же время вы также не хотите, чтобы вам выдавалось исключение ValueError. Даже если вы посмотрите, может войти другой программист и непреднамеренно добавить отрицательную переменную, тогда ваш код выдаст ошибку. Чтобы предотвратить это безумие, вы можете использовать abs():

abs()Функция будет принимать в своём значении и перевести его к абсолютному значению (81 в данном случае). Затем в sqrt()функцию будет передано неотрицательное абсолютное значение, что нам и нужно, чтобы не получить надоедливых ошибок!

Понимание списка и sqrt ()

Что делать, если у вас есть несколько чисел, квадратные корни которых вы хотели бы получить? Вы можете вычислить квадратный корень для всего в одной строке с помощью встроенного цикла for, который называется составлением списка.

Сначала составьте список значений, квадратные корни которых вы хотите получить.

Во-вторых, давайте переберём список с помощью выражения для цикла, чтобы получить квадратный корень для каждого значения. Синтаксис встроенного выражения цикла for — это число в числах, где «число» — это каждый член списка, который мы назвали «числами». Мы сохраним результаты в списке, который мы назовём «квадратные числа».

squaredNumbers = [ math.sqrt(number) for number in numbers]

Используйте print()оператор, чтобы увидеть результаты возведения списка чисел в квадрат.

for-утверждения и sqrt ()

Вы также можете использовать типичный цикл for. Хотя использование типичного цикла for означает, что вам нужно написать больше строк кода, чем в приведённом выше примере, некоторые люди могут легче читать циклы for.

Сначала объявите список, в котором вы хотите сохранить вычисленные значения.

Мы будем использовать тот же список значений («числа»), что и в предыдущем примере, и перебираем каждый из его элементов, которые мы назвали «число».

for number in numbers:
squaredNumbers.append(math.sqrt(number))

Теперь, если вы распечатаете этот новый список чисел в квадрате, вы получите тот же результат, что и в предыдущем примере.

Пример с sqrt (): диагональные расстояния

Есть много вариантов использования sqrt(). Одним из примеров является то, что вы можете использовать его для определения диагонального расстояния между двумя точками, которые пересекаются под прямым углом, например, углами улиц или точками на поле или на схеме.

Это потому, что диагональное расстояние между двумя точками, которые пересекаются под прямым углом, было бы эквивалентно гипотенузе треугольника, и для этого вы можете использовать теорему Пифагора (a 2 + b 2 ) = c 2, которая, как правило, использует квадратные корни. Эта формула очень удобна, потому что на городских улицах, домашних чертежах и в полях можно легко получить измерения длины и ширины, но не для диагоналей между ними.

Вам нужно будет использовать sqrt()гипотенузу c 2, чтобы получить длину. Другой способ переписать теорему Пифагора — c = √a 2 + b 2. Давайте представим, что мы проехали по трассе в нашем местном парке в форме треугольника.

Мы пробежали по длине и ширине, а затем вернулись к исходной точке. Чтобы точно подсчитать, сколько футов вы пробежали, вы можете рассчитать футы диагонального пути, который вы пересекаете, используя длину и ширину (чью длину в футах вы можете сохранить как переменные «a» и «b») парк:

Результатом будет 47.43416490252569. Итак, когда вы добавляете это к двум другим длинам, вы знаете, и вот оно. Общее количество футов, которое вы пробежали по дорожке в форме прямоугольного треугольника в парке.

Что ещё можно сделать с помощью Sqrt ()?

Теперь, когда вы знаете основы, возможности безграничны. Например:

В этой статье вы узнали, как использовать sqrt()списки с положительными и отрицательными числами и как переработать теорему Пифагора, чтобы выполнить четыре математических вычисления sqrt().

Источник

Как вычислить квадратный корень в Python

В Python есть предопределенная функция sqrt(), которая возвращает квадратный корень числа. Она определяет квадратный корень из значения, которое умножается на само себя и дает число. Функция sqrt() не используется напрямую для нахождения квадратного корня из заданного числа, поэтому нам нужно использовать математический модуль для вызова функции sqrt() в Python.

Например, квадратный корень из 144 равен 12.

Использование метода math.sqrt()

Функция sqrt() – это встроенная функция, которая возвращает квадратный корень из любого числа. Ниже приведены шаги, чтобы найти квадратный корень из числа.

Давайте напишем программу на Python.

Давайте создадим программу на Python, которая находит квадратный корень десятичных чисел.

В следующей программе мы прочитали число от пользователя и нашли квадратный корень.

Использование функции math.pow()

Pow() – это встроенная функция, которая используется в Python для возврата степени числа. У него два параметра. Первый параметр определяет число, а второй параметр определяет увеличение мощности до этого числа.

Использование оператора **

Мы также можем использовать оператор экспоненты, чтобы найти квадратный корень из числа. Оператор может применяться между двумя операндами. Например, x ** y. Это означает, что левый операнд возведен в степень правого.

Ниже приведены шаги, чтобы найти квадратный корень из числа.

Давайте реализуем вышеуказанные шаги.

Как мы видим в приведенном выше примере, сначала мы берем ввод(число) от пользователя, а затем используем оператор степени **, чтобы узнать степень числа. Где 0,5 равно √(символ корня), чтобы увеличить степень данного числа.

Давайте создадим программу Python, которая находит квадратный корень из указанного диапазона, в следующей программе вычисление из всех чисел от 0 до 50.

Источник

Как извлечь корень в Python (sqrt)

Но обо всём по порядку.

Что такое квадратный корень

Корнем квадратным из числа «X» называется такое число «Y», которое при возведении его во вторую степень даст в результате то самое число «X».

Операция нахождения числа «Y» называется извлечением квадратного корня из «X». В математике для её записи применяют знак радикала:

Нотация питона отличается в обоих случаях, и возведение в степень записывается при помощи оператора » ** «:

a = 2 b = a ** 2 print(b) > 4

import math import random # пример использования функции sqrt() # отыщем корень случайного числа и выведем его на экран rand_num = random.randint(1, 100) sqrt_rand_num = math.sqrt(rand_num) print(‘Случайное число = ‘, rand_num) > Случайное число = 49 print(‘Корень = ‘, sqrt_rand_num) > Корень = 7.0

Квадратный корень

Положительное число

import math print(math.sqrt(100)) > 10.0

А можете — из вещественных:

import math print(math.sqrt(111.5)) > 10.559356040971437

Легко проверить корректность полученных результатов с помощью обратной операции возведения в степень:

print(math.sqrt(70.5)) > 8.396427811873332 # возвести в степень можно так print(8.396427811873332 ** 2) > 70.5 # а можно с помощью функции pow() print(pow(8.396427811873332, 2)) > 70.5

Отрицательное число

Функция sqrt() не принимает отрицательных аргументов. Только положительные целые числа, вещественные числа и ноль.

Такая работа функции идёт вразрез с математическим определением. В математике корень спокойно извлекается из чисел меньше 0. Вот только результат получается комплексным, а таким он нужен для относительно узкого круга реальных задач, вроде расчетов в сфере электроэнергетики или физики волновых явлений.

print(math.sqrt(-1)) > ValueError: math domain error

Функция sqrt() корректно отрабатывает с нулём на входе. Результат тривиален и ожидаем:

Кубический корень

Само название функции sqrt() намекает нам на то, что она не подходит для извлечения корня степени отличной от двойки. Поэтому для извлечения кубических корней, сначала необходимо вспомнить связь между степенями и корнями, которую продемонстрируем на корне квадратном:

# Квадратный корень можно извлечь с помощью операции возведения в степень «**» a = 4 b = a ** 0.5 print(b) > 2.0

👉 Таким образом, извлечь кубический корень в Python можно следующим образом:

Корень n-степени

То, что справедливо для корня третьей степени, справедливо и для корней произвольной степени.

# извлечём корень 17-й степени из числа 5600 x = 5600 y = 17 z = pow(x, (1/y)) print(z) > 1.6614284717080507 # проверяем корректность результата print(pow(z, y)) > 5600.0

Но раз уж мы разбираемся с математической темой, то попытаемся мыслить более обобщённо. С помощью генератора случайных чисел с заданной точностью будем вычислять корень случайной степени из случайного числа:

import random # точность можно задать на ваше усмотрение x = random.randint(1, 10000) y = random.randint(1, 100) z = pow(x, (1 / y)) print(‘Корень степени’, y, ‘из числа’, x, ‘равен’, z) # при проверке вероятны незначительные расхождения из-за погрешности вычислений print(‘Проверка’, pow(z, y)) # но специально для вас автор накликал целочисленный результат > Корень степени 17 из числа 6620 равен 1.6778624404513571 > Проверка 6620.0

Решение реальной задачи с использованием sqrt

Корень — дитя геометрии. Когда Пифагор доказал свою знаменитую теорему, людям тут же захотелось вычислять стороны треугольников, проверять прямоту внешних углов и сооружать лестницы нужной длины.

Соотношение a2 + b2 = c2, где «a» и «b» — катеты, а «c» — гипотенуза — естественным образом требует извлекать корни при поиске неизвестной стороны. Python-а под рукой у древних греков и вавилонян не было, поэтому считать приходилось методом приближений. Жизнь стала проще, но расчет теоремы Пифагора никто не отменял и в XXI веке.

📡 Решим задачку про вышку сотовой связи. Заказчик требует рассчитать высоту сооружения, чтобы радиус покрытия был 23 километра. Мы неспешно отходим на заданное расстояние от предполагаемого места строительства и задумчиво смотрим под ноги. В голове появляются очертания треугольника с вершинами:

Модель готова, приступаем к написанию кода:

Расчёт выполнен, результат заказчику предоставлен. Можно идти пить чай и радоваться тому, что теперь ещё больше людей смогут звонить родным и сидеть в интернете.

Источник

Извлечение корня в Python

В этой статье мы рассмотрим, как извлечь корень в Python, а также какой модуль и функция для этого используется. Но давайте обо всем по порядку.

Если мы знаем только общую площадь квадрата и хотим узнать размер одной его стороны либо же собираемся рассчитать расстояние между 2-мя точками в декартовых координатах, нам потребуется квадратный корень. Это не проблема, если речь идет о математике. Но что делать, когда речь идет о языке программирования? К нашему счастью разработчики Python предусмотрели для решения вышеописанной задачи специальную функцию. Но прежде чем продолжить, давайте немного вспомним теорию.

Квадратный корень — что это?

Квадратным корнем, полученным из числа «A», называют число «B», которое при возведении во 2-ю степень даст в итоге то самое изначальное число «A».

Непосредственную операцию, позволяющую найти значение «B», называют извлечением корня из «A». Математики применяют для обозначения этой операции специальный знак (его еще называют знаком радикала):

Когда речь идет о корне в «Питоне», ситуация обстоит иначе, причем в обоих случаях. К примеру, само возведение числа в степень записывают посредством оператора «**«:

Ответ в консоли «Пайтона» будет равняться четырем.

Касаемо квадратного корня, то он в Python представлен функцией sqrt(). Однако она существует не сама по себе, а в рамках соответствующего математического модуля math. Таким образом, перед началом работы этот модуль надо будет импортировать, но это абсолютно не сложно сделать на практике:

import math

Идем дальше. Наша функция sqrt() принимает лишь один параметр – значение, из которого нам надо извлечь √. Давайте напишем простенький код и задействуем float в качестве типа данных возвращаемого значения.

import math

import random

# попробуем функцию sqrt() на практике

# найдем корень случайного числа с последующим выводом его на экран

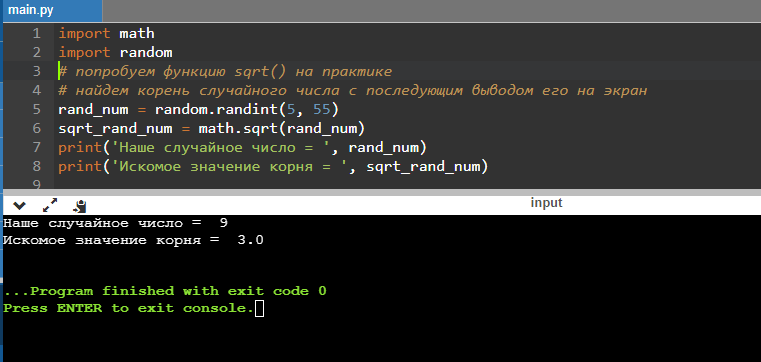
rand_num = random.randint(5, 55)

print(‘Наше случайное число = ‘, rand_num)

print(‘Искомое значение корня = ‘, sqrt_rand_num)

Вы можете попробовать работу этого кода у себя на компьютере или на любом онлайн-компиляторе. Вот, к примеру, компилятор для Python 3.

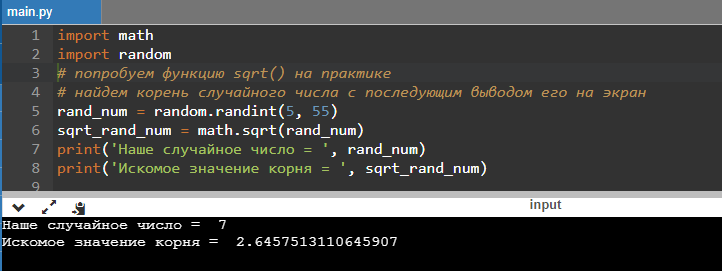
Результат может быть таким:

Так как мы используем модуль random, результат будет различаться при каждом выполнении кода.

Но никто не мешает сделать все намного проще:

Положительные числа

Функция sqrt() предназначена для работы с положительными значениями. Если число больше либо равно нулю, то неважно, какой тип данных у него, ведь извлечение корня возможно как из целых, так и из вещественных чисел.

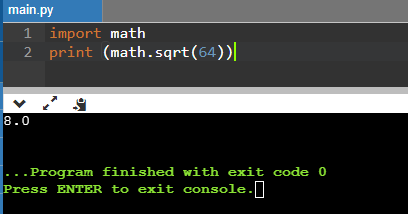
Из целых:

Из вещественных:

Сомневаетесь в корректности итоговых результатов предыдущего примера? Просто выполните обратное возведение в степень:

Также не забывайте, что сделать это можно и посредством специальной функции pow:

Отрицательные значения и ноль

Функция sqrt в «Питоне» — вещь полезная и знать ее нужно, однако она не принимает отрицательного числа — лишь положительные (целые и вещественные), а также ноль.

Такая ограниченная возможность использования не соответствует математическим канонам, ведь в реальной жизни специалисты по математике без проблем извлекают √ и из отрицательных значений. Да, результат будет комплексным и пригодится лишь для решения довольно узкого спектра задач, типа расчетов волновых явлений в физике либо вычислений в энергетической сфере.

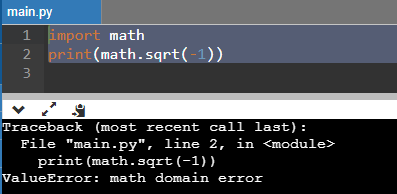
Учитывайте вышесказанное, если пытаетесь извлекать корни в Python посредством этой функции. Передав отрицательное значение, вы получите error:

А вот если говорить про ноль, то ошибки не будет, так как код отработает корректно. Однако результат тут очевиден, поэтому практическая ценность данной возможности весьма условна:

Хотите знать о «Питоне» намного больше? Добро пожаловать на специализированный курс в «Отус»!

Источник

Три или четыре способа извлечь корень

Речь в первую очередь идёт о корректности (точности вычислений). Производительность на втором месте.

2 ответа 2

Ещё можно посмотреть в какой код переводятся эти варианты и убедиться, что код разный:

P.S. Ну и, конечно, если нужно получить сразу много корней, то лучше использовать векторизованный Numpy для этого. Использование для задачи range/sqrt/sum векторизированных функций даёт 50-кратное ускорение:

Если коротко, то разница в реализации. И очевидно в скорости выполнения, входных и выходных параметрах. А вообще-то интересно заглянуть, что там во встроенных функциях.

pow(x, n)

math.sqrt()

math.pow()

И немного документации math.pow(). Здесь хотелось бы перевести одно заключение из документации:

В отличие от встроенного оператора **, math.pow () преобразует оба своих аргумента в тип float. Используйте ** или встроенную функцию pow () для вычисления точных целочисленных степеней.

Можно сделать вывод, что под каждую конкретную задачу может быть подобран оптимальная функция для вычислений. Думаю, что тема достаточно обширна и можно исследовать, например, скорости для вычисления в том или ином случае.

Все вышеописанное для версии python 3.х.x.

Для pow() были найдены данные строки

Для math.pow() реализация немного интересней:

Можно копать дальше, не уверен есть ли необходимость. Но инетересно же) можно так же увидеть еще одну интересную реализацию для long_pow() здесь

Источник