Как посчитать количество изоморфных графов
4. Изоморфные графы. Алгоритм распознования изоморфизма графов.
Изоморфные графы.
Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.
Из определения следует, что изоморфные графы можно одинаково изображать графически и отличаться они будут только метками вершин.
Изоморфизм графов есть отношение эквивалентности.
Алгоритм распознования изоморфизма графов.
Критерий изоморфности неориентированных графов
Неориентированные графы G и H с конечным числом вершин изоморфны тогда и только тогда, когда матрицы смежности A(G) и A(H) этих графов связаны соотношением 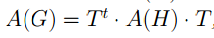
Теорема. Для того, чтобы граф G1 был изоморфен графу G2, необходимо и достаточно выполнения следующих условий:
1. Полустепени входа и исхода соответствующих вершин равны.
2. Существует подстановка, переводящая граф G1 в граф G2.
Cформулируем алгоритм распознавания изоморфизма двух графов G1 и G2:
Как посчитать количество изоморфных графов
Рассматривается эвристический алгоритм проверки графов на изоморфность. Проведён анализ работы алгоритма и проверка корректности на персональном компьютере.
Граф или неориентированный граф G — это упорядоченная пара G := (V,E), для которой выполнены следующие условия:
Один из способов представления графов – матрица смежности. Пусть граф имеет N вершин. Тогда матрица смежности будет иметь размер N x N, где значение ячейки в i-ой строке и j-ом столбце равно единице в случае достижимости j-ой вершины из i-той через одно ребро или нулю, если i-ая вершина не связана ребром с j-ой вершиной.
Граф G называется изоморфным графу H, если существует биекция f из множества вершин графа G в множество вершин графа H, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f(A) в вершину f(B) и наоборот — если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f − 1(A) в вершину f − 1(B). В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра. Здесь будут рассмотрены только неориентированные невзвешенные графы.
Полный перебор
Находятся все перестановки вершин одного из графов. Для каждой перестановки сравниваются множества рёбер графов. Если хотя бы одна перестановка даст полное совпадение множеств рёбер – графы изоморфны.
Оптимизация для частных случаев. Очевидно, что нет смысла ставить в соответствие вершины с различными степенями. Тогда перестановки будем делать только для вершин с одинаковыми степенями
Степень вершины – количество рёбер, содержащих данную вершину.
Эвристический алгоритм проверки графов на изоморфность
Алгоритм использует одно из свойств матрицы смежности. Значение в ячейке (i, j) показывает количество различных путей, содержащих ровно одно ребро, по которым можно попасть из i-ой вершины в j-ую вершину. При возведении матрицы в N-ую степень значение в ячейке (i, j) будет показывать количество различных путей длиной в N рёбер, по которым можно попасть из i-ой вершины в j-ую вершину.
Путь в графе G = (V,E) — последовательность вершин при \(v_i\) принадлежащем к V при i = 1, …, k, таких, что две любые последовательные вершины соединены хотя бы одной дугой из E.
Введём несколько понятий.
Уникальная характеристика ребра – набор из N чисел, которые показывают количество путей ведущих из одной вершины ребра в другую вершину ребра и содержащих ровно 1, 2 … N рёбер для каждого из N чисел соответственно.
Уникальная характеристика вершины – сортированный набор из N уникальных характеристик рёбер, содержащих данную вершину и вершины от 1-ой до N-ой вершины соответственно.
Уникальная характеристика графа – сортированный набор из N уникальных характеристик вершин от 1-ой до N-ой вершины соответственно.
Для определения изоморфности двух графов достаточно проверить на равенство их уникальные характеристики.
Сравнение работы переборного и эвристического алгоритма
Переборный алгоритм находит все перестановки вершин. Количество перестановок из N вершин – N! Следовательно, время работы алгоритма прямопропорционально факториалу количества вершин. Дополнительной памяти алгоритм не требует.
Время работы алгоритма с полным перебором:
| Количество вершин | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Время проверки | 1мс | 1мс | 3мс | 3мс | 39мс | 281мс | 2с 503мс | 30с 439мс | 6м 28с |
Время работы эвристического алгоритма:
| Количество вершин | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Время проверки | 4мс | 113мс | 472мс | 1c 677мс | 4c 624мс | 11с | 22с | 42c | 1м 12c | 3м 29c |
Проверка корректности работы эвристического алгоритма на персональном компьютере
Если эвристический алгоритм дал отрицательный результат, значит, графы точно не изоморфны. Иначе требуется дополнительная проверка.
1) Проверка сравнением результатов, полученных полным перебором и эвристическим алгоритмом.
Даёт абсолютно точную оценку. Недостаток метода – невозможность проверки алгоритма на больших графах в связи с медленной работой переборного алгоритма.
2) Проверка нахождением биекции (перестановки) вершин.
Возьмём две вершины, у которых уникальные характеристики равны. Пусть это будет первая вершина. Следующие вершины будем выбирать так, чтобы они имели одинаковые уникальные характеристики для всех рёбер между уже выбранными вершинами.
Понятно, что если графы не изоморфны, то никакой алгоритм не сможет найти биекцию, ставящую графы в соответствие. Остаётся рассмотреть один случай, когда эвристический алгоритм дал положительный результат, а биекция, ставящая граф в соответствие другому не найдена.
Находились все графы данной размерности, сортировались по уникальным характеристикам, сравнивались между собой только характеристики находящиеся в списке рядом.
Зависимость количества графов, имеющих различные матрицы смежности от количества вершин в графе
| Количество вершин | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Количество графов | 1 | 2 | 8 | 64 | 1 024 | 32 768 | 2 097 152 | 268 435 456 | 68 719 476 736 |
Для более эффективной проверки вводились следующие оптимизации:
1) Пред. расчёт уникальных характеристик графа для уменьшения времени проверки (не надо повторно вычислять уникальные характеристики для сравниваемых графов).
2) Проверка наборов графов только с одинаковым возрастающим набором степеней вершин для уменьшения используемой памяти (не надо хранить в памяти все графы одновременно).
| Все графы | Только с одинаковым возрастающим набором степеней вершин | |
|---|---|---|
| Пред. расчёт уникальных характеристик графа | Метод 1 | Метод 3 |
| Сравнение «на лету» | Метод 2 | Метод 4 |
Время проверки при различных методах:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Метод 1 | 5мс | 7мс | 12мс | 34мс | 410мс | -память | |||
| Метод 2 | 3мс | 7мс | 14мс | 53мс | 1с 730мс | 2м 38с | -память | ||
| Метод 3 | 6мс | 7мс | 15мс | 20мс | 56мс | 630мс | 19с 687мс | -память | |
| Метод 4 | 8мс | 9мс | 14мс | 20мс | 67мс | 1с 230мс | 1м 6с | 1ч 46м | -время |
При проведении проверки не нашлось ни одной пары графов, для которой бы алгоритм дал неверный результат.
Проверка изоморфности двух графов и поиск изоморфных подграфов: подход на основе анализа NB-Paths
Есть такая задача – проверить, являются ли два графа изоморфными друг другу. Т.е., говоря по-простому, узнать, являются ли оба эти графа «одним и тем же» графом, но с разной нумерацией вершин и, в случае задания графов графически, с разным их пространственным расположением. Решение этой задачи не является таким уж очевидным, как может кому-то показаться на первый взгляд: даже для небольших графов взгляд на их графическое представление не всегда даст однозначный ответ. См., например, рисунок в той же Вики: ru.wikipedia.org/wiki/Изоморфизм_графов#Пример.
А есть и более сложная задача: поиск в некотором «большом» графе всех подграфов, изоморфных некоторому другому графу «поменьше». Это еще более «темный лес». То есть, конечно, не совсем темный, но задача, согласитесь, не самая простая.
Итак, что же мы имеем?
1. Зачем вообще все это надо
И хотя задача про изоморфные (под)графы, как мы уже упомянули, сложная, она довольно нужная и полезная. А зачем? А затем, например, чтобы искать в базе данных химические соединения, подобные некоторой заданной молекуле по ее структурной формуле. Ведь ее можно представить себе в виде графа, не так ли? Этим занимается хемоинформатика – есть такая наука. А ведь есть еще задачи сопоставления с образцом, различные биоинформатические задачи, да много всего интересного.
2. Как решают эту задачу?
Классический подход к решению данной задачи был заложен Дж. Ульманом в 1976 году [3], впоследствии он существенно доработал свой алгоритм [4]. Также данный подход получил дальнейшее развитие в работах многих других авторов, например, Корделлы и соавторов [2] (алгоритм VF2), Бонници и соавторов [1] (алгоритм RI), и др.
Если кратко, то суть этого подхода заключается в «умном переборе» возможных соответствий вершин графа-образца B и графа A, в котором идет его поиск. «Умным» этот перебор делает ввод различных условий и ограничений, которые позволяют как можно раньше отсечь неподходящие варианты. Также для этих целей может проводиться различная предварительная обработка исходных данных.
Не будем здесь заниматься пересказом данных работ, а предложим читателю познакомиться с ними самостоятельно. Однако «показ лучше наказа», и, нужно отметить, что в Сети есть и неплохие графические примеры и объяснения этих алгоритмов. См., например, следующие:
coderoad.ru/17480142/Есть-ли-простой-пример-для-объяснения-алгоритма-Ульмана – очень хорошее и понятное объяснение с примером,
issue.life/questions/8176298 – шаги алгоритма VF2 с примером.
Однако возникает вопрос – возможны ли также еще какие-либо иные пути и подходы для решения этой задачи, пусть и для каких-то частных случаев? И вот с одним из возможных ответов на этот вопрос и хотелось бы Вас познакомить.
3. Изоморфизм графов и NB-пути
Давайте сразу договоримся: под NB-путями (и не из англомании, а просто потому, что так – короче) мы будем называть maximal non-branching paths, т.е. максимально протяженные неразветвляющиеся пути некоторого графа.
Итак, если у нас если два графа изоморфны друг другу, то для любого представления первого графа в виде последовательности максимально протяженных неразветвляющихся путей (т.е. этих наших NB-путей) всегда существует соответствующее ему такое же представление второго графа, и при этом:
Таким образом, задачу проверки изоморфизма двух графов можно решить нахождением таких соответствующих друг другу путей и, затем, проверкой равенства друг другу матриц смежности, построенных исходя их сохранения порядка вершин в полученных последовательностях путей (при этом каждая вершина добавляется в порядок следования единожды, при ее первом «упоминании»). В нашем примере для построения матриц смежности будут использоваться следующие порядки вершин:
A: 1, 2, 6, 4, 5, 3
B: 3, 4, 5, 1, 2, 6
Матрица смежности для A для заданного порядка вершин:
Матрица смежности для B для заданного порядка вершин:
Матрицы равны, следовательно, графы A и B – изоморфны.
При этом данный подход (1) применим как для ориентированных, так и неориентированных графов, (2) применим для графов, содержащих более одной компоненты связности/ сильной связности, (3) применим для графов, содержащих кратные (множественные) ребра и петли, однако (4) не учитывает вершины, для которых отсутствуют инцидентные им ребра.
4. Ну хорошо, проверили изоморфизм графов. А что же с поиском подграфов?
А тут, честно признаюсь, все значительно сложнее. Тут у нас будет следующее ограничение: исходя из самой сути метода можно находить не любые, но лишь «вписанные» подграфы. А «вписанным» подграфом графа A мы будем называть такой его подграф, который может быть «приклеен» к другим частям графа A только за счет ребер, инцидентных лишь граничным вершинам его (подграфа) неразветвляющихся путей максимальной длины (при этом граф A может содержать и иные компоненты связности). Не волнуйтесь, ниже будет пример, и все будет понятней. Прим. С 12.2020 все же удалось доработать данный метод для поиска всех (а не только «вписанных») подграфов, изоморфных данному. Но об этом в самом конце (см. Раздел 8. Вместо послесловия – Продолжение).
Кроме того, при решении данной задачи, помимо поиска соответствий NB-путей графов A и B по длине (как это было в рассмотренном выше примере с проверкой изоморфизма), также необходимо отдельно искать и следующие возможные соответствия между ними:
При поиске «вписанного» изоморфного подграфа графа B в графе A (см. рис. выше) будут обнаружены следующие соответствия:
A1 = <0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 9->10>
A2 = <0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 10->11>
A3 = <0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 12->13>
A4 = <0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 13->14>
A5 = <0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 14->12>
Однако, если мы добавим к графу A дополнительное ребро 3->8, у нас получится граф A’ (ниже на том же рисунке). И в A’ уже будет не найти «вписанных» подграфов, изоморфных графу B. Действительно: ребро 3->8 «разбивает» путь 2->3->4 графа A на два и, значит, путей-кандидатов для внутреннего пути 2->3->4 графа B обнаружено не будет.
5. Теперь сам алгоритм
Теперь мы можем перейти к более детальному рассмотрению алгоритма поиска «вписанных» в граф А подграфов, изоморфных некоторому графу B.
Итак, алгоритм будет состоять из 4-х этапов:
Этап I. Препроцессинг
На данном этапе мы находим все NB-пути по каждому из графов, а также оцениваем факторы, ограничивающие пространство выбора при переборе. Т.е. мы делаем следующее:
Этап II. Сопоставление
На данном этапе мы будем подбирать NB-пути-кандидаты (далее – просто «пути-кандидаты») из графа A для каждого из NB-путей графа B. Отметка о каждом пути-кандидате из PathsA для каждого i-го пути PathsB[i] будет записываться в двумерный динамический массив (в C++ – в вектор векторов) NPaths – соответственно в i-й вектор (i-ю строку) – в виде упорядоченного триплета чисел: номер соответствующего пути в PathsA – номер стартовой позиции в нем – длина пути.
Например, PathsB[2] = <1, 0, 3, 3, 1, 3>означает, что пути PathsB[2] сопоставлено 2 пути-кандидата из A: из PathsA[1] – 3 первых элемента пути начиная с нулевого (начального), и из PathsA[3] – также 3 элемента начиная с первого (следующего за начальным).
При этом поиск (подбор) путей-кандидатов мы будем производить по 4-м направлениям:
Предварительное прореживание
Теперь давайте попробуем «ужать» граф A. Оставим в нем лишь те ребра, которые вошли в найденные нами пути-кандидаты. Если при этом граф A потерял хоть бы одно ребро по сравнению с его изначальным состоянием – возвращаемся на этап I “Препроцессинг”: степени вершин графа A и, соответственно, перечень путей-кандидатов может быть уменьшен и, соответственно, может быть сокращено пространство поиска.
Этап III. Прореживание перечня путей-кандидатов
Целью настоящего этапа является дальнейшее максимально возможное исключение неподходящих путей кандидатов. Для этого осуществим следующие действия.
Т.е., грубо говоря, мы выкидываем те пути-кандидаты, которые заведомо не войдут в искомые подграфы – исходя из расстояния до всех прочих путей-кандидатов (страшно далеки эти пути от всех прочих), исходя из их цикличности/ нецикличности, а также исходя из должного равенства/ неравенства их граничных вершин с граничными вершинами других путей-кандидатов.
Если по результатам этапа III хотя бы 1 путь-кандидат был удален из PathsA, то – опять же – обновляется граф А – в нем остаются только те ребра, которые вошли в оставшиеся пути-кандидаты. И, опять же, если при этом граф A «похудел» хотя бы на одно ребро – снова возвращаемся на этап I “Препроцессинг”: степени вершин графа A и, соответственно, перечень путей-кандидатов может быть уменьшен и, соответственно, может быть сокращено пространство поиска.
Этап IV. Заключение
Каждое возможное сочетания всех оставшихся путей-кандидатов задает подграф графа A. Для каждого такого подграфа строится матрица смежности с учетом порядка следования путей кандидатов таким же образом, как была построена матрица смежности B0 для графа B, а затем эти матрицы смежности сравниваются между собой.
Если они равны, то сравниваются кратности ребер (см. п. 3 Этапа I Препроцессинг). Если все эти условия выполнены – найденный подграф считается изоморфным графу B и добавляется в множество найденных результатов.
При проведении этапа IV “Заключение” возможно применение различных дополнительных проверок, ускоряющих выявление и отбрасывание неподходящего подграфа.
6. Как все запутано… Рассмотрим пример работы алгоритма
Не знаю как Вам, а мне без примера было бы непонятно. Давайте рассмотрим все на примере.
На рис. ниже приведены графы A = <1->2, 2->5, 5->15, 16->15, 5->5, 5->5, 5->4, 5->6, 7->6, 6->8, 6->6, 6->9, 9->10, 9->11, 12->0, 0->12, 4->13, 13->14, 14->4> и B = <1->1, 4->5, 5->1, 1->3, 3->3, 3->2, 2->7, 2->8, 9->10, 10->9, 1->6, 6->11, 11->12, 12->6>. Нашей задачей является нахождение в графе A всех «вписанных» подграфов, изоморфных графу B. Результат также отражен на рисунке: найденные вершины и ребра графа A выделены толстой линией, а номера соответствующих вершин графа B указаны в скобках (если вариантов несколько – они указываются через дробь).
При решении задачи поиска в графе A «вписанных» подграфов, изоморфных графу B, имеем следующие результаты работы алгоритма.
Этап I: Выполнены все действия и расчеты по п.п. 1-5 данного этапа, ниже приводятся полученные PathsA и PathsB.
Этапы II-III. Сопоставление показало, что для каждого пути из PathsA находится как минимум один путь-кандидат из PathsB, а по результатам предварительного прореживания PathsA был сокращен. На этапе основного прореживания (III) дальнейшего сокращения PathsA не произошло. В результате PathsA и PathsB приняли вид:
Итоговое сопоставление NPaths имеет вид:
NPaths:
i=0: 3 0 2
i=1: 4 0 2
i=2: 2 0 2
i=3: 7 0 2 8 0 2
i=4: 7 0 2 8 0 2
i=5: 6 0 2
i=6: 5 0 2
i=7: 0 0 3
i=8: 1 0 4
i=9: 9 0 3
Здесь самое время вспомнить, что каждый упорядоченный триплет чисел в NPaths[i] задает соответствующий PathsB[i] путь-кандидат из A в формате: номер соответствующего пути из PathsA – стартовая позиция отрезка из данного пути – длина отрезка. Таким образом, нетрудно убедиться, что пути PathsB[0] = <1->1> (i=0: 3 0 2) соответствует единственный путь из A, а именно: отрезок из пути PathsA[3], начинающийся с его самого начала и имеющий длину 2.
Этап IV. В результате в графе A был найден единственный подграф A1, изоморфный графу B. A1 = <0->12, 1->2, 2->5, 4->13, 5->4, 5->5, 5->6, 6->6, 6->9, 9->10, 9->11, 12->0, 13->14, 14->4>.
7. Что же дальше?
А, дальше, в принципе, и все. Хотя не совсем: автор должен признаться, что алгоритм может еще дорабатываться и дорабатываться. Что тут нужно добавить?
8. Вместо послесловия – Продолжение
В декабре 2020 случилось то, что должно было случиться: удалось как адаптировать данный подход для поиска всех (а не только «вписанных») подграфов в графе по образцу, так и воплотить это на практике. Решение, в принципе, лежало на поверхности: вместо non-branching paths (нет короткого аналога термина по-русски) были взяты сами ребра графов. И с января 2021 также на практике была реализована функция, позволяющая искать изоморфные подграфы с учетом меток вершин, причем произвольного типа (в т.ч. — строкового, что позволяет использовать «многогранные» метки; возможно, это может оказаться полезным для различных задач, в том числе, в области химии).
Как проверить на изоморфизм 2 графа?
Проверить планарность графа
Проверить нужно граф на то, что он планарный или нет (если да, то по возможности нарисовать без.
Нахождение фактора графа и остова графа для некоторого произвольного графа (5-6 вершин)
Форумчане прошу помощь в выполнение задания по деск. мат. Задание: Нахождение фактора графа и.
Либо найти преобразование из одного графа в другой, либо найти инвариант, разный у двух графов.
В данном случае, например, у первого графа есть цикл длины 3, а все циклы второго графа исключительно чётной длины.
Хотя для меня более наглядным является то замечание, что второй граф является двудольным, а первый — нет.
Добавлено через 4 минуты
Задача об эффективном алгоритме может обсуждаться в разделе Алгоритмы и является одной из самых сложных задач.
А неэффективный алгоритм очевиден:
1. составляются матрицы смежности nxn
2. для каждой перестановки n из n! вариантов проверяется, что
3. переименование вершин первого графа не даст второй, т.е. Q T AQ=B, где A и B — матрицы смежности, Q — единичная матрица с переставленными строками в соответствии с перестановкой.
Поднимаю тему, есть рекурсивный алгоритм проверки на изоморфизм 2-х графов.
Пусть есть 2 графа, с матрицами смежности вершин.
X=
01 11111000000000
10 11000111000000
1101000000111000
1110000000000111
1000011100100100
1000101010010010
1000110001001001
0100100011100100
0100010101010010
0100001110001001
0010100100011100
0010010010101010
0010001001110001
0001100100100011
0001010010010101
0001001001001110
Y=
01 11111000000000
10 11000111000000
1100100100110000
1100010010001100
1010001000101010
1001001000010101
1000110001000011
0110000001010110
0101000001101001
0100001110000011
0010100010011001
0010010100100101
0001100010100110
0001010100011010
0000101101001100
0000011011110000
и проверяется соответствие между вершинами-
Если соответствующие элементы матриц подграфов равны, то переходим к следующему подграфу из 3-х вершин
Здесь же мы откатываемся к n-1 вершинам в случае если соответствующие элементы матриц подграфов не равны, т.е. к двум вершинам и производим перестановку.
и т.д. для любых подграфов до n вершин производим проверку на изоморфизм. Т.е. на подграфах с k вершинами, в случае отсутствия соответствия переходим к подграфам с k-1 вершинами и делаем перестановки, проверяя равенство A T *A*X = Y,
Поправьте, если я не прав, т.к. сомневаюсь что это верно.
Но ведь, если каждая строка матрицы Q содержит только один элемент = 1, в то время, как все остальные элемент = 0, то мы не получим те же строки (с элементами равными соответствующим им элементам в матрице A) в матрице B.
Приведу щас свой алгоритм написанный на python (это алгоритм Ульмана)

