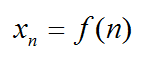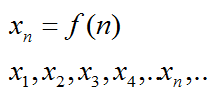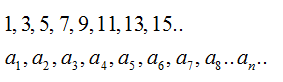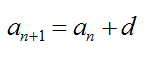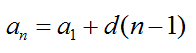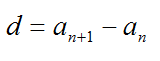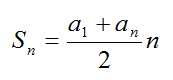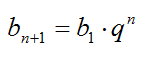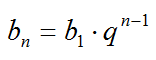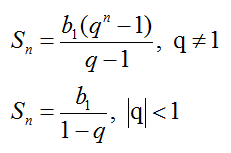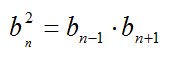Как посчитать количество чисел в последовательности
Количество чисел в последовательности
С клавиатуры вводится последовательность целых чисел. Признаком окончания ввода является отрицательное число в потоке ввода. Определите количество чисел в введенной последовательности.
Выходные данные
Вывести количество чисел в последовательности.
Дана последовательность из 11 чисел. Вычислить количество тех элементов последовательности, которые меньше 2
Нужна помощь с решением: Дана последовательность из 11 чисел. Вычислить количество тех элементов.
Определить в заданной последовательности целых чисел количество чисел Фибоначчи
Определить в заданной последовательности целых чисел количество чисел Фибоначчи.
Вывести количество отрицательных чисел последовательности
Помогите составить програмку в JAVA Eclipse,которая бы выводила количество отрицательных чисел.
Определить какое количество отрицательных чисел записано в начале последовательности
дана последовательность из N вещественных чисел, начинающихся с отрицательного числа. Определить.
Числовая последовательность
Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: \(2; 4; 6; 8; 10. \) А правило «первое число равно \(3\), а каждое следующее число в два раза больше предыдущего» формирует последовательность: \(3; 6; 12; 24; 48. \)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами (или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности \(3; 6; 12; 24; 48…\) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность \(3; 6; 12; 24; 48…\) обозначить как \(a_n\), то можно записать, что \(a_1=3\), \(a_2=6\), \(a_3=12\), \(a_4=24\) и так далее.
порядковый номер элемента
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
— I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Отметим, что последовательности в начале статьи заданы именно словесным способом.
— II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: \(b_n=\frac
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: \(a_n=8+5n-n^2\). Вычислите \(a_9\).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер \(n=9\). Подставляем в формулу: \(a_9=8+5·9-9^2=8+45-81=-28\).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: \(c_1=4\), \(c_
Решение: Первый член нам известен: \(c_1=4\).
Второй мы получим, подставив в формулу вместо \(n\) единицу: \(c_<1+1>=c_1+3\)
\(c_2=c_1+3=4+3=7\)
Третий (\(n=2\)): \(c_<2+1>=c_2+3 \)
\(c_3=c_2+3=7+3=10\).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула \(c_
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента \(z_1=2;\) \(z_2=5\). Так же известна формула следующего элемента \(z_
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
Последовательность на данный момент:
Так как формула дана для элемента с номером \(n+2\), то чтобы найти \(z_3\) нужно подставлять вместо \(n\) единицу:
\(z_<1+2>=3z_<1+1>-z_1\)
\(z_3=3z_2-z_1=3·5-2=13\)
| \(z_1\) | \(z_2\) | \(z_3\) | \(z_4\) | \(z_5\) | \(. \) |
| \(2\) | \(5\) | \(13\) | ? | ? | \(. \) |
\(z_<2+2>=3z_<2+1>-z_2\)
\(z_4=3z_3-z_2=3·13-5=34\)
| \(z_1\) | \(z_2\) | \(z_3\) | \(z_4\) | \(z_5\) | \(. \) |
| \(2\) | \(5\) | \(13\) | \(34\) | ? | \(. \) |
\(z_<3+2>=3z_<3+1>-z_3\)
\(z_5=3z_4-z_3=3·34-13=89\)
| \(z_1\) | \(z_2\) | \(z_3\) | \(z_4\) | \(z_5\) | \(. \) |
| \(2\) | \(5\) | \(13\) | \(34\) | \(89\) | \(. \) |
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности \(a_n=n^2-n\):
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
\(a_2=2^2-2=2\) – тоже не то.
Нужный элемент найден.
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
Если число \(3\) – член последовательности, то значит при некотором значении \(n\), формула \(\frac<51+2n>
Подставляем тройку вместо \(a_n\).
Числовые последовательности для чайников: определение, формулы
По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.
Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.
Последовательности чисел
Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.
Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.
Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.
Что такое числовая последовательность?
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.
Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.
На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.
Какие бывают последовательности
Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.
Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.
Арифметическая прогрессия
Посмотрим на числа:
Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.
Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:
Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.
Сумма первых n членов прогрессии вычисляется по формуле:
Также африфметическая прогрессия обладает характреристическим свойством:
Геометрическая прогрессия
Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:
Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:
Сумма первых n членов прогрессии:
Характеристическое свойство геометрической прогрессии:
Способы задания последовательностей
Последовательность можно задать несколькими способами:
Предел последовательности
Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.
Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.
Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.
Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел.
Что нужно помнить, вычисляя пределы последовательностей
Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.
Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором.
Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.
Подсчитать количество каждого числа в последовательности
Для каждого числа от M до N подсчитать количество его делителей
Для каждого числа от M до N подсчитать количество его делителей. Добавлено через 45 минут.
Zodt, это я сам учу
Добавлено через 1 минуту
Даценд, а вы можете мой код посмотреть и подсказать что добавить после присваивания k? Пожалуйста.
Согласен, мне следовало удалить повторы в последовательности.
я не являюсь профессиональным программистом.
Для каждого числа последовательности найти количество цифр 0 и 1.
Поступает последовательность целых положительных чисел, 0—конец последовательности. Для каждого.
Для каждого числа последовательности найти количество цифр 5
Вводится последовательность из N целых чисел. Для каждого числа последовательности найти количество.
Как указать количество повторений каждого числа в последовательности?
Подскажите, как указать количество повторений каждого числа в последовательности? Задача С.
Для каждого числа последовательности найти количество его делителей
Доброго времени суток всем! Возникла проблема с данной программой : Вводится последовательность.
За один проход
Среди задач по программированию часто попадаются такие: дана последовательность однотипных элементов (обычно это числа), требуется за один проход по ней найти какую-нибудь характеристику (среднее квадратическое отклонение, количество минимальных элементов, непрерывный участок с наибольшей суммой. ) Дополнительное ограничение — последовательность может быть очень длинной, и в память не поместится. Других ограничений на элементы последовательности, обычно, не накладывается.
С этими задачами всё, более или менее, понятно: нужно найти то, что на мехмате МГУ называют «индуктивным расширением» искомой функции, и реализовать её вычисление. Если найти не удалось (требуемый объём памяти слишком велик), то задача не решается.
Но попадаются и другие задачи. В них есть дополнительные ограничения на элементы последовательности в совокупности, и эти ограничения приходится существенно использовать для решения (и проверять их не надо). Простейшая такая задача выглядит так:
Задача 1. В последовательности записаны целые числа от 1 до N в произвольном порядке, но одно из чисел пропущено (остальные встречаются ровно по одному разу). N заранее неизвестно. Определить пропущенное число
Решение очевидно: просматриваем числа, находим их количество K и сумму S. По условию, N=K+1, значит, сумма чисел от 1 до N будет равна (K+1)*(K+2)/2, и пропущенное число равно (K+1)*(K+2)/2-S. Если вы почему-то боитесь переполнений, то работайте с беззнаковыми числами (там переполнения не страшны — но будьте осторожны при вычислении (K+1)*(K+2)/2 🙂 ), или вместо суммы ищите XOR всех чисел.
Задача 2. В последовательности записаны целые числа. Одно из чисел встречается ровно один раз, остальные — по два раза. Найти число, которое встречается один раз.
Здесь тоже всё просто: найдем XOR всех чисел — он и будет ответом. В самом деле, если какой-то бит в искомом числе равен нулю, то во всей последовательности он будет равен 1 в чётном числе элементов, и его значение в XOR равно нулю. В противном случае, аналогично, его значение в XOR равно 1. Или, проще говоря, одинаковые элементы при суммировании взаимоуничтожатся.
Слегка усложним задачу:
Задача 3. В последовательности записаны целые числа. Число X встречается один или два раза, остальные числа — по три раза. Найти число X. Для простоты считаем, что числа неотрицательные.
А если сделать ещё один шаг?
Задача 4. В последовательности записаны целые числа. Число X встречается 1,2 или 3 раза, остальные числа — по 4 раза. Найти число X.
Предыдущий подход здесь уже не сработает: если мы возьмём систему счисления с основанием 4, и найдём поразрядные суммы, то для случаев, когда X встретился один или три раза, всё будет хорошо. Но если X встретился дважды, мы уже не сможем узнать, была ли очередная цифра равна 0 или 2 — значение суммы si для этого разряда в обоих случаях будет равно нулю. Что делать?
На самом деле, в прошлый раз я вас обманул. Совершенно незачем возиться с троичной системой — достаточно было посчитать сумму битов в каждом двоичном разряде, и если она делилась на 3, то в числе X соответствующий бит равнялся нулю. Если нет — то единице.
В этой задаче делаем точно так же, но проверяем делимость на 4. Например, эти задачи можно решить так:
Задача 5. В длинной очереди стоят люди. Для каждого из них, кроме последнего, записали его имя и имя того, кто стоит за ним. Полученные записи перемешали и записали в файл. Требуется за один просмотр файла определить имена первого и последнего человека. Известно, что эти имена различны (иначе задача неразрешима), но, в общем, имена могут повторяться. Имя каждого человека состоит из шестнадцати 8-битных символов.
С помощью этого приёма можно, также, найти разность множеств, одно из которых получается из другого добавлением двух или даже трёх элементов (или добавлением двух и удалением одного). Если различия более сильные, приходится хранить суммы конъюнкций не только пар, но и троек битов. И XOR там уже недостаточно — приходится считать хотя бы трёхбитные знакопеременные суммы.
UPD: В обсуждении этой задачи в комментариях SeptiM предложил более простое решение. Рассматриваем имена как 128-битные целые числа (xi,yi), и считаем суммы S1=sum(xi-yi), S2=sum(xi^2-yi^2) (первая сумма должна быть знаковой 129-битной, вторая — знаковой 257-битной. Переполнения игнорируем, работаем по модулю 2^129 и 2^257 соответственно). Понятно, что их значения равны S1=x1-xn, S2=x1^2-xn^2, где x1 — первое имя, xn — последнее. Отсюда легко находим x1=(S1+S2/S1)/2, xn=x1-S1.
Задача 6. В последовательности записаны целые числа, больше половины из которых равны одному и тому же числу X. За один просмотр последовательности найти это число.
Заметим, что если мы вычеркнем из последовательности два различных числа, то условие задачи останется верным. Поэтому мы можем вычёркивать пары различных чисел до тех пор, пока все элементы не станут равными одному и тому же числу. Это число и будет X.
Чтобы реализовать этот метод, заведём ячейку, в которой будет храниться какой-то элемент последовательности, и счётчик — сколько копий этого элемента у нас просмотрено и пока не вычеркнуто.
Когда мы читаем очередной элемент, у нас есть три варианта:
— Счётчик равен нулю. Кладём прочитанный элемент в ячейку, увеличиваем счётчик на 1.
— Элемент равен значению ячейки. Увеличиваем счётчик на 1.
— Элемент не равен значению ячейки. Уменьшаем счётчик на 1.
После того, как мы просмотрим всю последовательность, в ячейке окажется искомое число.
К сожалению, обобщить это решение на случай, когда число X встречается больше, чем в 1/k случаев (k известно), не удаётся. Мы можем так же завести k-1 ячейку со счётчиком, удалять за один раз по k различных элементов, получим в конце k-1 кандидата на роль X, но опознать его нам не удастся — даже значение счётчика у него будет не самым большим. Зато если нам разрешат сделать второй проход, мы можем посчитать, сколько раз каждый из кандидатов встретился в последовательности, и выдать гарантированно самого частого.
У исходной задачи есть ещё одно решение. Для каждого бита считаем, сколько раз он равнялся 0, а сколько — 1, и выдаём более частое значение. Возможно, его удастся обобщить на случай, когда X встречается больше, чем в 1/3 случаев — посчитаем статистику для каждой пары битов… вдруг поможет?
Следующие две очень похожие задачи за один проход решить вряд ли получится. Но для них есть интересное решение за log(M) проходов.
Задача 7. В последовательности записаны целые неотрицательные числа, меньшие M, причём известно, что каждое число встречается не более одного раза. Найти наименьшее число, которое в этой последовательности не встречается.
Задача 8. В последовательности записано M+1 целое неотрицательное число, все числа меньше M. Найти какое-нибудь число, которое встречается хотя бы дважды.
Есть ещё задачка, которая меня давно интересует, но решения которой я не знаю.
Задача 9. В последовательности записаны числа от 1 до N в каком-то порядке. Каждое число встречается один раз. N заранее известно. Требуется за один просмотр последовательности определить чётность записанной в ней перестановки. Какой минимальный объём памяти для этого требуется?
Парадокс заключается в том, что в любой заранее выбранный момент нам достаточно помнить 1 бит информации. Но после этого будет необходимо иметь N+1 бит — чтобы запомнить, какие элементы идут в последовательности после этого момента.