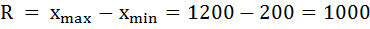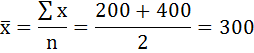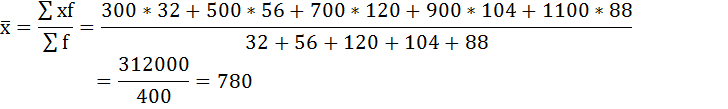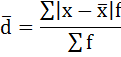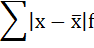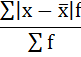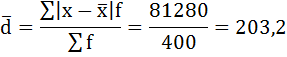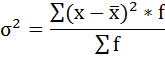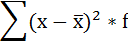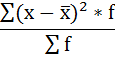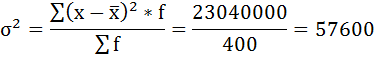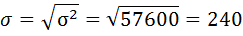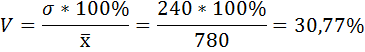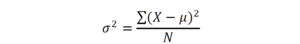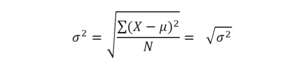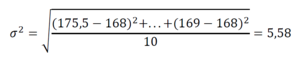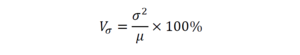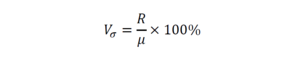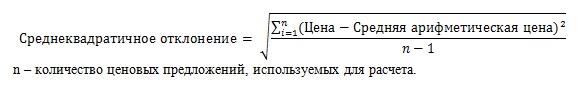Как посчитать коэффициент вариации пример
Задача №6. Расчёт показателей вариации
По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
Определите:
2) средний размер вклада;
3) среднее линейное отклонение;
5) среднее квадратическое отклонение;
6) коэффициент вариации вкладов.
Решение:
Данный ряд распределения содержит открытые интервалы. В таких рядах условно принимается величина интервала первой группы равна величине интервала последующей, а величина интервала последней группы равна величине интервала предыдущей.
Величина интервала второй группы равна 200, следовательно, и величина первой группы также равна 200. Величина интервала предпоследней группы равна 200, значит и последний интервал будет иметь величину, равную 200.
1) Определим размах вариации как разность между наибольшим и наименьшим значением признака:
Размах вариации размера вклада равен 1000 рублей.
2) Средний размер вклада определим по формуле средней арифметической взвешенной.
Предварительно определим дискретную величину признака в каждом интервале. Для этого по формуле средней арифметической простой найдём середины интервалов.
Среднее значение первого интервала будет равно:
Занесём результаты вычислений в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Итого | 400 | — | 312000 |
Средний размер вклада в Сбербанке города будет равен 780 рублей:
3) Среднее линейное отклонение есть средняя арифметическая из абсолютных отклонений отдельных значений признака от общей средней:
Порядок расчёта среднего линейонго отклонения в интервальном ряду распределения следующий:
1. Вычисляется средняя арифметическая взвешенная, как показано в п. 2).
2. Определяются абсолютные отклонения вариант от средней:
3. Полученные отклонения умножаются на частоты:
4. Находится сумма взвешенных отклонений без учёта знака:
5. Сумма взвешенных отклонений делится на сумму частот:
Удобно пользоваться таблицей расчётных данных:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | 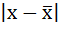 | 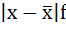 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Итого | 400 | — | — | — | 81280 |
Среднее линейное отклонение размера вклада клиентов Сбербанка составляет 203,2 рубля.
Расчёт дисперсии в интервальных рядах распределения производится по формуле:
Порядок расчёта дисперсии в этом случае следующий:
1. Определяют среднюю арифметическую взвешенную, как показано в п. 2).
2. Находят отклонения вариант от средней:
3. Возводят в квадрат отклонения каждой варианты от средней:
4. Умножают квадраты отклонений на веса (частоты):
5. Суммируют полученные произведения:
6. Полученная сумма делится на сумму весов (частот):
Расчёты оформим в таблицу:
| Размер вклада, руб. | Число вкладчиков, f | Середина интервала, х |  | 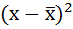 | 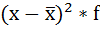 |
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Итого | 400 | — | — | — | 23040000 |
5) Среднее квадратическое отклонение размера вклада определяется как корень квадратный из дисперсии:
По величине коэффициента вариации можно судить о степени вариации признаков совокупности. Чем больше его величина, тем больше разброс значений признаков вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя.
Расчет коэффициента вариации
Понятие коэффициента вариации
В статистике под вариацией величин того или иного показателя в совокупности понимается различие его уровней у тех или иных единиц анализируемого состава в один и тот же период либо момент исследования. В том случае, когда выполняется анализ отличий величин показателя у одного и того же предмета, у одной и той же единицы совокупности в различные периоды или моменты времени, то это будет уже именоваться не вариацией, а колебаниями или изменениями в течении определенного периода.
Размещено на www.rnz.ru
Формула расчета коэффициента вариации
Являясь отношением среднего квадратического отклонения к средней величине, в общем случае анализируемый показатель вычисляется по следующей формуле:
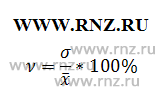
Вычисление рассматриваемого показателя посредством расчета отклонений от средней величины отражает его объективное содержание, но его получение достаточно трудоемко, и для повышения точности выводов требуются расчеты среднего показателя и отклонений без округлений или со значительным количеством цифр после запятой. Поэтому в практических вычислениях делимое может быть вычислено с использованием другой, полученной из общей, формуле вычисления среднего квадратического отклонения в форме разности среднего квадрата элемента и квадрата среднего значения. Таким образом, формула расчета исследуемого показателя, дающая более точный результат, выглядит следующим образом:

Пример расчета коэффициента вариации
Приведем пример расчета коэффициента вариации цены. Исходные данные для вычисления коэффициента вариации и необходимые промежуточные расчеты приведены в таблице:
Для вычисления используем следующую формулу:
Определим средне значение: хсреднее = (17,74 + 13,69 + 16 + 11,87 + 11,21 + 15,09 + 19,49 + 19,97 + 17,03) / 9 = 15,79 руб.
Среднее квадратическое отклонение: σ = √(77,79 / 9) = 2,94.
Коэффициент вариации: ν = 2,94 / 15,79 * 100 = 18,62%.
Интерпретация. Полученное значение исследуемого показателя показывает, что колеблемость цены относительно небольшая и составляет 18,62% среднего уровня. Полученное значение также указывает на однородность исследуемой совокупности, т.к. полученное значение коэффициента вариации менее 33%.
Внимание! Расчет коэффициента вариации по 44 ФЗ имеет свои особенности, поэтому приводим отдельный пример расчета коэффициента вариации по 44 ФЗ
Онлайн калькулятор расчета коэффициента вариации
В заключении приводим небольшой онлайн калькулятор расчета коэффициента вариации онлайн, используя который, Вы можете самостоятельно выполнить расчет указанного показателя онлайн. При заполнении формы калькулятора расчета коэффициента вариации онлайн внимательно соблюдайте размерность полей, что позволит выполнить вычисления онлайн быстро и точно. Дробные величины должны вводиться с точкой, а не с запятой! В форме онлайн калькулятора уже содержатся данные условного примера, чтобы пользователь мог посмотреть, как работает онлайн калькулятор расчета коэффициента вариации. Для расчета данного показателя по своим данным просто внесите их в соответствующие поля формы онлайн калькулятора и нажмите кнопку «Выполнить расчет». Обратите внимание, что расчет коэффициента вариации онлайн калькулятором осуществляется только по несгруппированным данным.
Онлайн-калькулятор расчета коэффициента вариации:
Коэффициент вариации в статистике: примеры расчета

Показатели описательной статистики
Существует несколько показателей, которые использует описательная статистика.
Среднее арифметическое
Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):
168, 171, 175, 177, 179, 187, 174, 176, 179, 169.
Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:
Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться. Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического. Если обратиться к росту студентов, то формула будет выглядеть следующим образом:
Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)
Если свести все к строгим математическим терминам, то определение среднего арифметического (обозначается греческой буквой – μ («мю»)) будет звучать так:
Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).
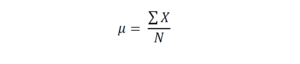
Стандартное отклонение
Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.
На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:
Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:
Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:
Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.
Коэффициент вариации
Среднее квадратичное отклонение хорошо работает с рядами, в которых разброс значений не очень велик (это хорошо прослеживалось на примере роста, где интервал был всего 18 см). Если бы ряд наших измерений был значительнее, а варьирование роста было сильнее, то стандартное отклонение стало непоказательным и нам потребовался бы критерий, который может отразить разброс в относительных единицах (т. е. в процентах, относительно средней величины).
Для этих целей предусмотрены абсолютные и относительные показатели вариации в статистике, характеризующие вариационные масштабы:
Квадратический коэффициент вариации (обозначается как Vσ) – это отношение среднеквадратичного отклонения к среднеарифметическому значению, выраженное в процентах.
Для нашего примера со студентами, определить Vσ несложно — он будет равен 3,18%. Основная закономерность – чем больше будет изменяться значение коэффициента, тем больше разброс вокруг среднего значения и тем менее однородна выборка.
Преимущество коэффициента вариации в том, что он показывает однородность значений (асимметрия) в ряду наших измерений, кроме того, на него не оказывают влияния масштаб и единицы измерения. Эти факторы делают коэффициент вариации особенно популярным в биомедицинских исследованиях. Будет считаться, что эксцесс значения Vσ =33% отделяет однородные выборки от неоднородных.
Если найти в ряду значений роста (первый пример) максимальное и минимальное значения, то получим размах вариации (обозначается как R, иногда ещё называется колеблемостью). В нашем примере – это значение будет равно 18 см. Эта характеристика используется для расчёта коэффициента осцилляции:
Коэффициент осцилляции – показывает как размах вариации будет относиться к среднему арифметическому ряда в процентном отношении.
Расчёты в Microsoft Ecxel 2016
Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:
| Наименование показателя | Расчёт в Excel 2016* |
| Среднее арифметическое | =СРГАРМ(A1:A10) |
| Дисперсия | =ДИСП.В(A1:A10) |
| Среднеквадратический показатель | =СТАНДОТКЛОН.В(A1:A10) |
| Коэффициент вариации | =СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10) |
| Коэффициент осцилляции | =(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10) |
* в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.
Итак, обобщим информацию:
Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила коэффициент вариации, который является мерой однородности данных.
Коэффициент вариации по 44-ФЗ. Пример расчёта, формула
Одной из ключевых стадий подготовки закупочной документации становится расчет начальной максимальной цены контракта (НМЦК). Законодательно предусмотрено несколько способов, с помощью которых можно производить расчеты. Чаще всего используется метод сопоставимых рыночных цен. При этом итоговая НМЦК должна определяться с учетом коэффициента вариации. Поэтому всем заказчикам необходимо понять, что включает в себя этот показатель и как его правильно определить.
Что такое коэффициент вариации
Размер НМЦК определяется еще на этапе планирования. Эта сумма должна быть отражена в плане и план-графике. Непосредственно перед подготовкой извещения она корректируется с учетом сложившейся на тот момент экономической обстановки. Вопросы, связанные с НМЦК рассматриваются в статье 22 44-ФЗ. Методики ее расчета описаны в Приказе Министерства экономики и развития № 567 от 02 октября 2013 года. В этом же документе приводятся правила определения коэффициента вариации.
Разработано несколько методик выявления НМЦК: нормативная, тарифная, проектно-сметная, затратная. Самым приоритетным считается метод сопоставимых рыночных цен. Именно его рекомендуется использовать при определении стартовой цены. Он предполагает сравнение коммерческих предложений, предоставляемых потенциальными поставщиками по запросу заказчика. Для проведения такого анализа и применяется коэффициент вариации. Он выражается в процентах.
Под коэффициентом вариации понимается мера относительного разброса предлагаемых цен. Он показывает, какую долю занимает средний разброс цен от среднего значения цены. Этот показатель может принимать следующие значения:
Для определения коэффициента разработана специальная формула. По ней легко подсчитать параметр, подставив соответствующие данные. Упростить себе задачу можно, используя калькуляторы, которые сегодня широко представлены в интернете.
Что делать, если коэффициент завышен
Если при расчете коэффициента вариации получилось значение меньше 33%, то выборка признается однородной. Следовательно, полученное значение можно использовать для определения НМЦК.
Если возникла такая ситуация, что значение коэффициента оказывается выше 33 процентов, тогда потребуется внесение корректировок в используемые данные. Для этого проводится дополнительное исследование рынка. Необходимо собрать коммерческие предложения от большего количества поставщиков и повторить расчет на основе новых данных. Если собрать дополнительные предложения не получается, можно воспользоваться сведениями из ранее заключенных договоров, которые хранятся в реестре контрактов.
В крайней ситуации, когда никак не получается добиться нужного коэффициента вариации можно исключить из выборки неподходящие предложения. Вы также можете попросить поставщика указать в своем предложении нужную вам сумму.
Правила расчета
Методика расчета коэффициента вариации прописана в приказе Минэкономразвития № 567. Согласно действующим нормам заказчик должен направить не менее пяти запросов коммерческих предложений потенциальным поставщикам. Для расчета используются не менее трех предложений, полностью соответствующих требованиям заказчика.
Стоит отметить, что приказ № 567 не является нормативным актом, следовательно, его исполнение не обязательно. За его нарушение никаких штрафных санкций не предусматривается. Однако во избежание спорных ситуаций заказчика рекомендуется пользоваться именно этими правилами расчета.
Для определения коэффициента вариации применяется следующая формула:
Среднеквадратичное отклонение позволяет определить разброс данных. Для его определения выбирают среднюю цену и меру разброса. Вычислить среднеквадратичное отклонение удается по следующей формуле:
В ситуациях, когда закупка включает в себя одновременно несколько позиций, расчет ведется по каждой из них. Это позволяет выявить товары с наибольшим разбросом цен.
Пример расчета
Предположим, что государственное учреждение проводит закупку принтеров для собственных нужд. Потенциальным поставщикам были отправлены соответствующие запросы. Было получено четыре коммерческих предложения цен: 2500 рублей, 2800 рублей, 2450 рублей и 2600 рублей.
В первую очередь необходимо рассчитать среднеарифметическое значение цены
Следующим шагом становится расчет среднеквадратичного отклонения
Осталось только рассчитать коэффициент вариации
Полученное значение коэффициента меньше 33%, следовательно, все собранные данные подходят для расчета стартовой цены контракта. Расчет НМЦК и коэффициента вариации оформляются в форме отчета, который становится обязательной частью закупочной документации.
Коэффициент вариации – важный инструмент, позволяющий оценить правильность ценовых предложений, полученных от поставщиков. Поэтому при составлении документации заказчикам необходимо учитывать правила расчета этого показателя и особенности его применения.