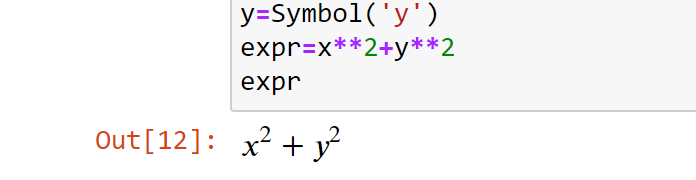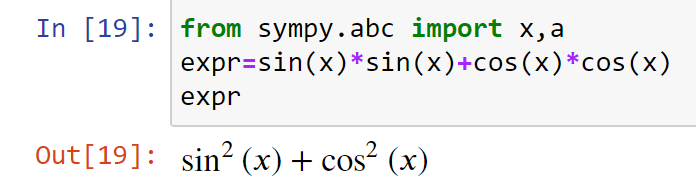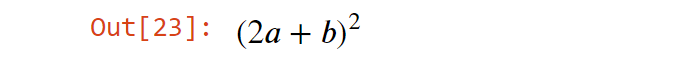Как посчитать интеграл в питоне
Библиотека Sympy: символьные вычисления в Python
Документацию и исходный код этой библиотеки можно найти на ее официальной странице.
Первые шаги с SymPy
Используем SymPy как обычный калькулятор
Как можно заметить, функция evalf() дает на выходе число с плавающей точкой.
Символы
В отличие от ряда других систем компьютерной алгебры, в SymPy можно в явном виде задавать символьные переменные. Это происходит следующим образом:
После их задания, с ними можно производить различные манипуляции.
Библиотека SymPy позволяет задавать форму вывода результатов на экран. Обычно мы используем формат такого вида:
Алгебраические преобразования
SymPy способна на сложные алгебраические преобразования. Здесь мы рассмотрим наиболее востребованные из них, а именно раскрытие скобок и упрощение выражений.
Раскрытие скобок
Чтобы раскрыть скобки в алгебраических выражениях, используйте следующий синтаксис:
При помощи ключевого слова можно добавить поддержку работы с комплексными переменными, а также раскрытие скобок в тригонометрических функциях.
Упрощение выражений
Вычисления
Вычисления пределов
Также можно вычислять пределы, которые стремятся к бесконечности.
Дифференцирование
Проверим результат последней функции при помощи определения производной через предел.
tan 2 (𝑥)+1 Результат тот же.
Разложение в ряд
Интегрирование
Также несложно посчитать интеграл и от специальных функций. Возьмем, например, функцию Гаусса:
Результат вычисления можете посмотреть сами. Вот примеры вычисления определенных интегралов.
Также можно вычислять определенные интегралы с бесконечными пределами интегрирования (несобственные интегралы).
Решение уравнений
Системы линейных уравнений
Факторизация
Булевы уравнения
Линейная алгебра
Матрицы
Матрицы в SymPy создаются как экземпляры класса Matrix :
И производить с ними разные манипуляции:
Дифференциальные уравнения
Теперь решим следующее дифференциальное уравнение:
Вычисление определённых интегралов: базовые алгоритмы

В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают «под капотом», и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.
Определение интеграла
Интегралом (по Риману) от функции на отрезке
называется следующий предел:
где — мелкость разбиения,
,
,
— произвольное число на отрезке
.
Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким. 
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).
Квадратурные формулы
Определение интеграла (1) можно переписать в виде
где — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа
точек, в которых вычисляется функция.
Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки и веса
таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.
Вычислительная задача
Задана функция , для которой есть алгоритм вычисления значений в любой точке отрезка
(имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).
Требуется найти приближённое значение интеграла .
Решения будут реализованы на языке Python 3.6.
Для проверки методов используется интеграл .
Кусочно-постоянная аппроксимация
Идейно простейшие квадратурные формулы возникают из применения выражения (1) «в лоб»:
Т.к. от метода разбиения отрезка точками и выбора точек
значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1)
; 2)
; 3)
.
Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.
Для анализа производительности квадратурных формул построим график погрешности в координатах «число точек — отличие численного результата от точного».
Что можно заметить:
Кусочно-линейная аппроксимация
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:

Иллюстрация метода трапеций для n=1 и n=2.
В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид
Построив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).
Контроль точности вычисления
Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.
Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.
Отсюда получаем следующий код для метода трапеций с контролем точности:
С таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.
Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.
Кусочно-параболическая аппроксимация

Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).
Приближая интеграл от функции на каждом из отрезков [xk;xk+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (xk+1=xk+h), получаем формулу Симпсона:
Из формулы (4) напрямую получается «наивная» реализация метода Симпсона:
Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.
Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :
Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.
Сравним эффективность метода трапеций и парабол:
Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).

Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.
Что дальше?
Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов wi в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.
Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:
На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.
Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.
Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.
Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:
Повторяя аналогичную процедуру для формулы Симпсона, получаем:
Если продолжить, вырисовывается такая таблица:
| 2 порядок | 4 порядок | 6 порядок | . |
|---|---|---|---|
| I0,0 | |||
| I1,0 | I1,1 | ||
| I2,0 | I2,1 | I2,2 | |
| . | . | . |
В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).
Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:
Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.
Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.
Дополнительный метод добавляется в класс Quadrature
Проверим, как работает аппроксимация высокого порядка:
Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:
Некоторые замечания
Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.
Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:
7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.
Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла и эквивалентного ему
. Как говорится, почувствуйте разницу.
Заключение
Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования «обычных» функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.
Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).
Integration ( scipy.integrate )В¶
General integration ( quad )В¶
This could be computed using quad :
The first argument to quad is a “callable” Python object (i.e. a function, method, or class instance). Notice the use of a lambda- function in this case as the argument. The next two arguments are the limits of integration. The return value is a tuple, with the first element holding the estimated value of the integral and the second element holding an upper bound on the error. Notice, that in this case, the true value of this integral is
is the Fresnel sine integral. Note that the numerically-computed integral is within \(1.04\times10^<-11>\) of the exact result — well below the reported error bound.
If the function to integrate takes additional parameters, the can be provided in the args argument. Suppose that the following integral shall be calculated:
This integral can be evaluated by using the following code:
is desired (and the fact that this integral can be computed as special.expn(n,x) is forgotten). The functionality of the function special.expn can be replicated by defining a new function vec_expint based on the routine quad :
An example of using double integration to compute several values of \(I_
As example for non-constant limits consider the integral
This integral can be evaluated using the expression below (Note the use of the non-constant lambda functions for the upper limit of the inner integral):
The integral from above
can be calculated as
Non-constant integration bounds can be treated in a similar manner; the example from above
can be evaluated by means of
which is the same result as before.
Gaussian quadrature¶
Romberg Integration¶
Integrating using Samples¶
For an odd number of samples that are equally spaced Simpson’s rule is exact if the function is a polynomial of order 3 or less. If the samples are not equally spaced, then the result is exact only if the function is a polynomial of order 2 or less.
This corresponds exactly to
whereas integrating the second function
does not correspond to
because the order of the polynomial in f2 is larger than two.
Faster integration using Ctypes¶
2x for trivial functions such as sine but can produce a much more noticeable increase (10x+) for more complex functions. This feature then, is geared towards a user with numerically intensive integrations willing to write a little C to reduce computation time significantly.
2.) Now compile this file to a shared/dynamic library (a quick search will help with this as it is OS-dependent). The user must link any math libraries, etc. used. On linux this looks like:
4.) Now integrate the library function as normally, here using nquad :
And the Python tuple is returned as expected in a reduced amount of time. All optional parameters can be used with this method including specifying singularities, infinite bounds, etc.
Ordinary differential equations ( odeint )В¶
For example suppose it is desired to find the solution to the following second-order differential equation:
with initial conditions \(w\left(0\right)=\frac<1><\sqrt[3]<3^<2>>\Gamma\left(\frac<2><3>\right)>\) and \(\left.\frac
Математическая библиотека Python SymPy
SymPy — это библиотека Python для выполнения символьных вычислений. Это система компьютерной алгебры, которая может выступать как отдельное приложение, так и в качестве библиотеки для других приложений. Поработать с ней онлайн можно на https://live.sympy.org/. Поскольку это чистая библиотека Python, ее можно использовать даже в интерактивном режиме.
В SymPy есть разные функции, которые применяются в сфере символьных вычислений, математического анализа, алгебры, дискретной математики, квантовой физики и так далее. SymPy может представлять результат в разных форматах: LaTeX, MathML и так далее. Распространяется библиотека по лицензии New BSD. Первыми эту библиотеку выпустили разработчики Ondřej Čertík и Aaron Meurer в 2007 году. Текущая актуальная версия библиотеки — 1.6.2.
Вот где применяется SymPy:
Установка SymPy
Такие дистрибутивы, как Anaconda, Enthough, Canopy и другие, заранее включают SymPy. Чтобы убедиться в этом, достаточно ввести в интерактивном режиме команду:
Исходный код можно найти на GitHub.
Символьные вычисления в SymPy
Символьные вычисления — это разработка алгоритмов для управления математическими выражениями и другими объектами. Такие вычисления объединяют математику и компьютерные науки для решения математических выражений с помощью математических символов.
Система компьютерной алгебры же, такая как SymPy, оценивает алгебраические выражения с помощью тех же символов, которые используются в традиционных ручных методах. Например, квадратный корень числа с помощью модуля math в Python вычисляется вот так:
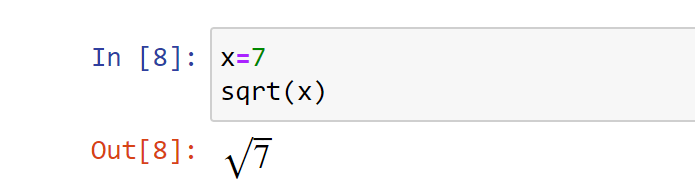
Как можно увидеть, квадратный корень числа 7 вычисляется приблизительно. Но в SymPy квадратные корни чисел, которые не являются идеальными квадратами, просто не вычисляются:
Это можно упростить и показать результат выражения символически таким вот образом:
В случае с модулем math вернется число, а вот в SymPy — формула.
Для рендеринга математических символов в формате LaTeX код SymPy, используйте Jupyter notebook:
Если выполнить эту команду в IDLE, то получится следующий результат:
Квадратный корень неидеального корня также может быть представлен в формате LaTeX с помощью привычных символов:
Символьные вычисления с помощью таких систем, как SymPy, помогают выполнять вычисления самого разного рода (производные, интегралы, пределы, решение уравнений, работа с матрицами) в символьном виде.
В пакете SymPy есть разные модули, которые помогают строить графики, выводить результат (LaTeX), заниматься физикой, статистикой, комбинаторикой, числовой теорией, геометрией, логикой и так далее.
Числа
Класс Float
Float представляет числа с плавающей точкой произвольной точности:
SymPy может конвертировать целое число или строку в число с плавающей точкой:
При конвертации к числу с плавающей точкой, также можно указать количество цифр для точности:
Для упрощения можно указать ограничение знаменателя:
Выведется дробь 1/5 вместо 3602879701896397/18014398509481984.
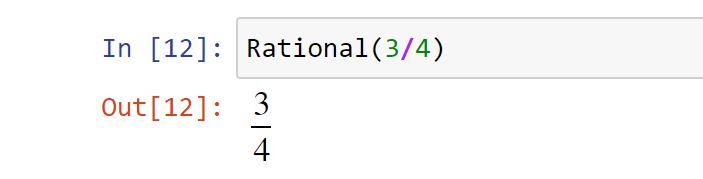
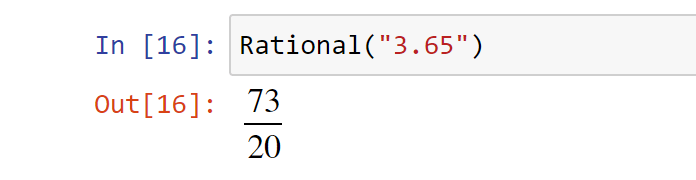
Если же в конструктор передать строку, то вернется рациональное число произвольной точности:
Также рациональное число можно получить, если в качестве аргументов передать два числа. Числитель и знаменатель доступны в виде свойств:
Класс Integer
Класс Integer в SymPy представляет целое число любого размера. Конструктор принимает рациональные и числа с плавающей точкой. В результате он откидывает дробную часть:
Бесконечность представлена в виде объекта-символа oo или как S.Infinity :
Символы
Аргумент функции Symbol() — это строка, содержащая символ, который можно присвоить переменной.
Код выше является эквивалентом этого выражения:
Символ может включать больше одной буквы:
В модуле abc можно найти элементы латинского и греческого алфавитов в виде символов. Таким образом вместо создания экземпляра Symbol можно использовать метод:
Смежные цифры справа берутся на 1 больше конечного значения.
Подстановка параметров
Одна из базовых операций в математических выражениях — подстановка. Функция subs() заменяет все случаи первого параметра на второй.
Этот код даст вывод, эквивалентный такому выражению.
Эта функция полезна, когда требуется вычислить определенное выражение. Например, нужно посчитать значения выражения, заменив a на 5 :
Это дает такой вывод:
Функция simplify()
Функция simplify() используется для преобразования любого произвольного выражения, чтобы его можно было использовать как выражение SymPy. Обычные объекты Python, такие как целые числа, конвертируются в SymPy.Integer и так далее. Строки также конвертируются в выражения SymPy:
Функция evalf()
Вычислим выражение с помощью evalf() и заменим r на 5:
По умолчанию точность после плавающей точки — 15, но это значение можно перезаписать до 100. Следующее выражение вычисляет, используя вплоть до 20 цифр точности:
Функция lambdify()
Функция lambdify() переводит выражения SymPy в функции Python. Если выражение, которое нужно вычислить, затрагивает диапазон значений, то функция evalf() становится неэффективной. Функция lambdify действует как лямбда-функция с тем исключением, что она конвертирует SymPy в имена данной числовой библиотеки, обычно NumPy. По умолчанию же она реализована на основе стандартной библиотеки math.
У выражения может быть больше одной переменной. В таком случае первым аргументом функции является список переменных, а после него — само выражение:
Логические выражения
Запросы
Следующие свойства предоставляют полезную информацию о выражении:
algebraic(x)
Чтобы быть алгебраическим, число должно быть корнем ненулевого полиномиального уравнения с рациональными коэффициентами. √2, потому что √2 — это решение x2 − 2 = 0. Следовательно, это выражения является алгебраическим.
complex(x)
Предикат комплексного числа. Является истиной тогда и только тогда, когда x принадлежит множеству комплексных чисел.
composite(x)
Предикат составного числа, возвращаемый ask(Q.composite(x)) является истиной тогда и только тогда, когда x — это положительное число, имеющее как минимум один положительный делитель, кроме 1 и самого числа.
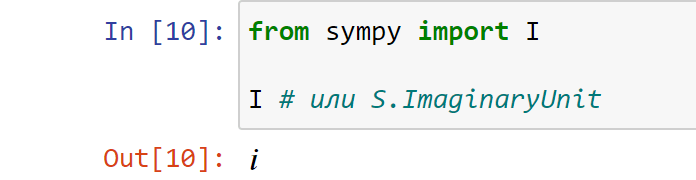
imaginary
Свойство представляет предикат мнимого числа. Является истиной, если x можно записать как действительное число, умноженное на мнимую единицу.
rational, irrational
Q.irrational(x) истинно тогда и только тогда, когда x — это любое реальное число, которое нельзя представить как отношение целых чисел. Например, pi — это иррациональное число.
positive, negative
Предикаты для проверки того, является ли число положительным или отрицательным.
zero, nonzero
Предикат для проверки того, является ли число нулем или нет.