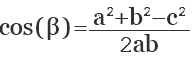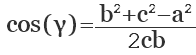Как посчитать градус угла в треугольнике

Углы треугольника

Геометрическая фигура из трех отрезков, соединенных между собой тремя точками, не лежащими на одной прямой, называется треугольником. Это — многоугольник с тремя углами. Сумма всех углов треугольника равна 180°. Если известна величина двух из них, третий угол определяем вычитанием из 180° величины двух известных углов.

α = 180°-β-γ

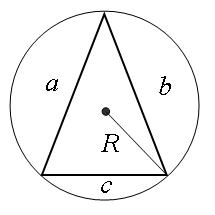
Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

a 2 = b 2 + c 2 + 2abc cos (α)

Отсюда, косинус искомого угла равняется сумме квадратов смежных сторон (b, с) минус квадрат третей стороны треугольника (а), противолежащей искомому углу, и все это делится на удвоенное произведение смежных сторон:

cos (α) = (b 2 + c 2 — a 2 ) / 2bc

,
где а, b, с — стороны треугольника.
Используя теорему косинусов, определяем косинусы остальных углов. Величины углов в градусах находим по тригонометрической таблице.

Источник

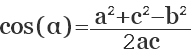
Решение треугольников онлайн

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

.

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:

.

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Источник

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Решение треугольников.

Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.

Эта математическая программа находит сторону \( c \), углы \( \alpha \) и \( \beta \) по заданным пользователем сторонам \( a, b \) и углу между ними \( \gamma \)

Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.

Введите стороны \( a, b \) и угол между ними \( \gamma \) Решить треугольник

Источник

Сторона треугольника через угол

Катет прямоугольного треугольника через угол и второй катет

Треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние.

Прямоугольный треугольник — это треугольник у которого один из углов прямой (равен 90°). Стороны треугольника образующие прямой угол называются катетами треугольника. Сторона противоположная прямому углу называется гиппотенузой.

Радиан — это угол, соответствующий дуге, длина которой равна её радиусу. Своё название данная едииница измерения получила от слова радиус. Имеет обозначение: рад, международное: rad.

Радианы являются основной единицей используемой в вичислениях.

Градус — общепринятая единица измерения плоского угла, которая равняется \dfrac<1> <90>части прямого угла или \dfrac<1> <360>часть окружности. В отличии от радиан, градусы являются чисто символическими единицами измерения, так сказать «взятые с потолка» и не имеют в своём значении ни какого математического основания.

Причина выбора градуса в качестве единицы измерения углов неизвестна. В быту измерение углов в градусах выглядит удобнее и понятнее, но что касается математических вычислений, то здесь основными единицами являются радианы.

Формула нахождения стороны через угол

Посчитать длину одного из катетов треугольника можно через второй катет и угол противолежащий искомой стороне:

Источник

Калькулятор сторон и углов треугольника

Треугольник ΔABC,
a = BC, b = AC, c = AB — стороны треугольника,

A = CAB, B = ABC, C = BCA − углы, противолежащие сторонам a, b, c соответственно.

Как пользоваться онлайн-калькулятором. В форме укажите три значения: одну сторону и 2 дополнительных параметра (например, угол и сторону, два угла или две стороны). Заполните поле «Текст с картинки». Нажмите «Решить».

Калькулятор треугольника нужен, если требуется найти решение треугольников – длины сторон и величину углов треугольника.

Решить треугольник − найти все углы и стороны треугольника. Данный калькулятор предназначен для нахождения элементов треугольника.

Как решить треугольник

Здесь размещен онлайн-калькулятор, с помощью которого можно решить треугольник по трем, двум сторонам и углам, по теореме синусов и косинусов, то есть показывается, как находить углы в треугольнике.

Решение треугольников можно находить с помощью таблицы Брадиса. Здесь ответ вычисляется автоматически компьютерной программой онлайн, быстро и удобно.

Если нужны формулы и решения задач на теоремы косинусов и синусов с ответами, то можно найти подробное и точное решение, если использовать бесплатный калькулятор треугольника.

В решении подробно показывается, как найти третью сторону по двум сторонам и углу между ними или как определить неизвестные стороны треугольника, если известна одна сторона.

Примеры решений практических задач

1) решить треугольник по двум сторонам и противолежащему углу, т.е. углу между ними. Даны стороны а = 12 см, b = 8 см, угол=60°. Для того, чтобы решить задачу, требуется указать в онлайн-форме на данной странице условия задачи. В поле для стороны «a» указывается 12, в поле для стороны «b» ставится 8, в поле для углов «A» указывается 60. Нажать «Решить».

В ходе решения задачи получаем ответ:
сторона c = 13,8 см;
угол B = 35,2644° = 35°15’52» = 35°16′ = 0,1959π = 0,6155 rad;
угол C = 84,7356° = 84°44’8» = 84°44′ = 0,4708π = 1,4789 rad;
Периметр = 33,8 см;
Полупериметр = 16,9 см;
Площадь = 47,7984 см 2 ;
Высота h_a = 7,9664 см;
Высота h_b = 11,9496 см;
Высота h_c = 6,9273 см;
Медиана m_a = 9,5513 см;
Медиана m_b = 12,2958 см;
Медиана m_c = 7,5107 см;
Радиус окружности R, описанной около треугольника = 6,9291 см;
Радиус окружности r, вписанной в треугольник = 2,8283 см.
Таким образом, был найден угол треугольника по двум сторонам и углу.

2) как найти угол треугольника, зная его стороны или решите треугольник по трем сторонам. Даны три стороны a = 2 см, b = 3 см, c = 4 см. В поле онлайн-формы «a» ставим 2, в поле «b» указываем 3, в поле «c» ставим 4. Далее следует нажать «Решить».

Используя теорему косинусов, получаем
угол A = 28,955° = 28°57’18» = 28°57′ = 0,1609π = 0,5054 rad;
угол B = 46,5675° = 46°34’3» = 46°34′ = 0,2587π = 0,8128 rad;
угол C = 104,4775° = 104°28’39» = 104°29′ = 0,5804π = 1,8235 rad;
Периметр = 9 см;
Полупериметр = 4,5 см;
Площадь = 2,9046 см 2 ;
Высота h_a = 2,9046 см;
Высота h_b = 1,9364 см;
Высота h_c = 1,4523 см;
Медиана m_a = 3,3912 см;
Медиана m_b = 2,7839 см;
Медиана m_c = 1,5811 см;
Радиус окружности R, описанной около треугольника = 2,0657 см;
Радиус окружности r, вписанной в треугольник = 0,6455 см.

Таким образом, были найдены все углы треугольника.

3) решить треугольник по двум углам и стороне. В треугольнике ABC сторона a = 5 см, два угла B = 30°, C = 45°.
Ответ:
сторона b = 2,59 см;
сторона c = 3,66 см;
угол A = 105° = 0,5833π = 1,8326 rad;
Периметр = 11,25 см;
Полупериметр = 5,625 см;
Площадь = 4,5785 см 2 ;
Высота h_a = 1,8314 см;
Высота h_b = 3,5355 см;
Высота h_c = 2,5019 см;
Медиана m_a = 1,9488 см;
Медиана m_b = 4,1857 см;
Медиана m_c = 3,537 см;
Радиус окружности R, описанной около треугольника = 2,588 см;
Радиус окружности r, вписанной в треугольник = 0,814 см.

Треугольники

Треугольник – многоугольник, который состоит из трех точек, соединенных тремя отрезками. Три точки в этом многоугольнике – вершины треугольника, а отрезки – стороны или ребра треугольника. На рисунке показан треугольник ΔABC, где A, B, C – его вершины, а AB, BC, AC – его стороны. Вершины треугольника дают треугольнику его обозначение. Угол при вершине A образуется сторонами AB и AC, обозначается как угол CAB.

Треугольники бывают разными. Название треугольников зависит от длины его сторон и величины его углов.

Стороны треугольника

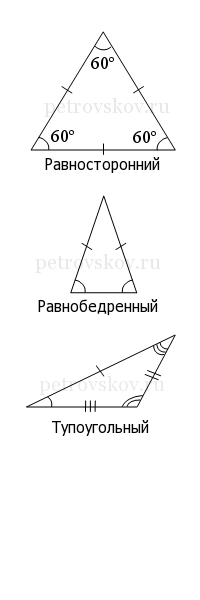
Равносторонний или правильный треугольник состоит из трех равных сторон и трех равных углов. Все три угла в равностороннем треугольнике равны 60 градусам.

Если в треугольнике две стороны имеют одинаковую длину, то это равнобедренный треугольник.
В равнобедренном треугольнике две равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.

Теоремы равнобедренных треугольников:
1) углы при основании равны,
2) если в треугольнике два угла равны, то это равнобедренный треугольник,
3) медиана, которая проведена к основанию, является биссектрисой и высотой.

Равные стороны в треугольниках обозначают одним, двумя или тремя штрихами или черточками, равные углы – одной, двумя или тремя дуговыми линиями.

Углы треугольника

Треугольники бывают остроугольными, тупоугольными и прямоугольными.

Треугольник является прямоугольным, если один из трех углов треугольника равен 90 градусам. Сторона, которая расположена напротив угла в 90 градусов, называется гипотенузой. Гипотенуза – самая большая сторона в прямоугольном треугольнике. Две другие стороны называются катетами.

Тупоугольный треугольник – треугольник, в котором один из углов больше 90 градусов.

Остроугольный треугольник – треугольник, в котором все три угла меньше 90 градусов.

Свойства треугольников

В треугольнике только один угол может быть больше 90 градусов.

В треугольнике сумма углов равна 180 градусам.

Внешний угол треугольника – смежный угол при этой вершине.
Варианты, как найти внешний угол при вершине:
а) суммировать два внутренних угла, не смежных с ним,
б) вычислить разность между 180 и внутренним углом этой вершины.

Если сложить любые две стороны треугольника, то сумма длин этих сторон всегда больше длины третьей стороны.

Радиус вписанной окружности

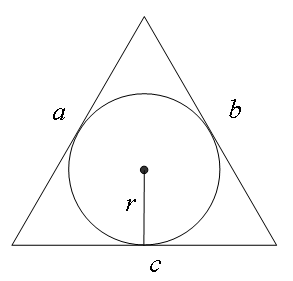
Окружность, вписанная в треугольник, – это круг, расположенный внутри треугольника.

Радиус этого круга (r) – отрезок, проведенный из центра вписанной окружности перпендикулярно к одной из сторон треугольника.

Центр вписанной окружности – точка пересечения двух биссектрис и равноудален от каждой стороны треугольника.

Для вычисления радиуса вписанной окружности используются площадь и периметр треугольника

Радиус описанной окружности

Окружность, описанная около треугольника, проходит через 3 вершины треугольника.

Для вычисления радиуса описанной окружности (R) используются площадь и длины всех сторон треугольника.

Источник