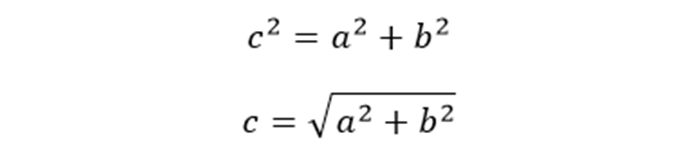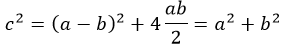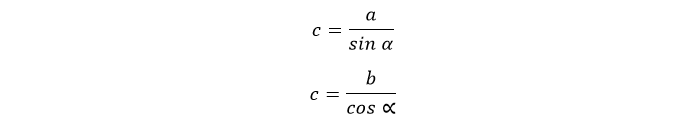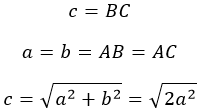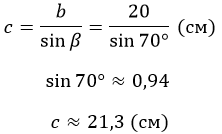Как посчитать гипотенузу равнобедренного треугольника
Формула гипотенузы равнобедренного прямоугольного треугольника
В повседневной жизни каждому человеку время от времени приходится решать задачи из школьной программы. Несмотря на то что многие в детстве считали эти знания ненужными, сейчас все понимают, что были неправы. Например, в любой момент может понадобиться найти длину гипотенузы равнобедренного треугольника, формулу расчета которой несложно вывести самостоятельно. Для этого следует вспомнить законы геометрии.
Законы геометрии
В первую очередь надо определиться с терминами. Чтобы в дальнейшем было понятно, что означают те или иные геометрические понятия, необходимо вспомнить следующие определения:
Треугольник – это замкнутая геометрическая фигура, состоящая из трех точек, соединенных последовательно тремя отрезками, которые являются сторонами этой фигуры. Прямые, исходящие из одной точки, образуют угол.
Каждый треугольник состоит из трех сторон. Исходящие из одной вершины стороны называются бедрами, поэтому фигура, у которой минимум две стороны имеют равную длину, называется равнобедренной. В случае когда все стороны фигуры равны, она называется равносторонним треугольником.
Треугольник, в котором есть прямой угол, называется прямоугольным. Прямым в геометрии называется угол в 90 градусов. Поскольку в каждой треугольной фигуре сумма всех углов равна 180 градусов, то в ней может быть только один прямой угол. Гипотенуза в переводе с греческого языка означает «натянутая» – это сторона треугольника, которая лежит напротив прямого угла.
Катет – это одна из двух других сторон прямоугольного треугольника, тоже греческое слово, которое в переводе означает опущенный, отвесный или перпендикуляр. Катеты одновременно являются бедрами, а в равнобедренном прямоугольном треугольнике гипотенуза служит еще и основанием.
Теорема – это истина, которую надо доказать. Одно из самых известных и значимых правил геометрии – это теорема Пифагора.
Теорема Пифагора
Древнегреческий математик и философ Пифагор, если верить историкам, первым нашел правильный расчет соотношения размеров длин катетов и гипотенузы. Согласно теореме Пифагора, длина гипотенузы в квадрате равна сумме длин катетов, возведенных в квадрат. Можно кратко описать теорему, обозначив гипотенузу буквой Г, а катеты — К1 и К2:
Как вычислить формулу
Если довериться логике и Пифагору, то легко высчитать, что размер самой длинной стороны треугольника будет равен квадратному корню из суммы квадратов двух меньших сторон. Если учесть, что в равнобедренном треугольнике катеты равны, то формулу можно усовершенствовать.
Гипотенузу равнобедренного треугольника можно рассчитать путем вычисления квадратного корня из квадрата длины катета, умноженного на два.
Вопрос на засыпку
Чтобы ответить на вопрос, как найти гипотенузу равностороннего треугольника, надо вспомнить, чему равен каждый его угол. При любой длине сторон в этой фигуре, сумма всех углов неизменна и равна 180 градусов, соответственно каждый из них в этой фигуре равен 60 градусов. Прямого угла в такой фигуре не может быть по определению, поэтому нет и гипотенузы. Значит, поставленный вопрос некорректен и не имеет ответа.
Практическое применение
В каких сферах повседневной жизни может понадобиться знание формулы? Эта тема находит практическое применение в архитектуре, строительстве, физике, математике, астрономии и других областях народного хозяйства, например:
Если внимательно оглядеться вокруг, можно различить большое количество разнообразных геометрических фигур.
Где геометрия, там и возможности использовать ее правила и формулы расчетов, в том числе и формулу длины гипотенузы.
Гипотенуза равнобедренного треугольника – формула
Гипотенуза это понятие из Греции, относящееся к треугольникам. К каким именно треугольникам относится это понятие, что оно обозначает, и когда его применять недопустимо говорим ниже.
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех вершин. Стороны образуют три угла при трех вершинах.
Для формулировки теорем требуется всем понятное обозначение сторон. Эти обозначения не должны быть классическими АВ или ВС, поскольку такие обозначения зависят от каждого конкретного ученика. Никто не вправе запретить решающему обозначать фигуру так, как это удобно лично ему. Например, именно по этой причине в математику было введено понятие основания треугольника. Вспомните, в равнобедренном треугольнике высота, проведенная к основанию, равняется биссектрисе и медиане. Формулировка четкая, понятная и простая для запоминания. Именно в этих целях и вводят дополнительные понятия.
Прямоугольный треугольник
Прямоугольный треугольник – это особенная фигура. Она имеет свои свойства и пропорции, один из углов такого треугольника всегда известен и равен 90 градусам, к тому же имеются специфические формулы площади и признаки равенства прямоугольных треугольников.
Рис. 2. Прямоугольный треугольник
В Древней Греции прямоугольным треугольникам уделяли особое внимание. Эти фигуры были предметом изучения не только математики, но и мореходства. С помощью подобных прямоугольных треугольников греки определяли расстояния в море. А в древних Сиракузах на основе системы прямоугольных треугольников была создана система прицеливания, с помощью которой город долгое время отбивался от атак врагов.
Греки особое внимание уделяли точности формулировок и потому придумали для сторон треугольников особые названия: гипотенуза для стороны, лежащей напротив прямого угла и катеты для сторон, прилежащих к прямому углу.
Если гипотенуза у равнобедренного треугольника? В общем случае, нет. В равнобедренном треугольнике есть только две боковые стороны и основание. Но если перед нами прямоугольный равнобедренный треугольник, то основание такого треугольника будет являться одновременно и гипотенузой. Найти ее можно как квадратный корень из удвоенного произведения катета – это следствие из теоремы Пифагора и равенства катетов, как боковых сторон равнобедренного треугольника.
$b=sqrt<2a>$ – где b это гипотенуза, а а – значение длины одного из катетов
Равносторонний треугольник
Стоит сказать и о равностороннем треугольнике, ведь это частный случай равнобедренного. Может ли существовать гипотенуза у равностороннего треугольника? Нет, поскольку гипотенуза возможна только в прямоугольном треугольнике, а в равностороннем треугольнике все углы всегда составляют 60 градусов, поэтому такой вариант невозможен вовсе.
Что мы узнали?
Мы узнали, зачем требуется большое количество определений. Поговорили о том, как получаются точные формулировки в геометрии, вспомнили древнегреческих ученых и рассказали, для чего они использовали знания о прямоугольных треугольниках. Выделили случаи, когда у равнобедренного треугольника может быть гипотенуза, а когда ее существование невозможно. А также поговорили о возможности существования гипотенузы у равностороннего треугольника.
Слово «гипотенуза» со школьных времен у многих вызывает негативные ассоциации. Добавим загадочного и непонятного. Происходит от греческого «ὑποτείνουσα».
А ведь означает всего-навсего «вытянутый». И речь идет о простейшей форме треугольника – прямоугольной (рис. 1).
Гипотенузой называют сторону напротив прямого угла. Самую протяженную. В данном случае – с. Остальные составляющие – катеты.
Простыми фигурами интересовались древние строители Вавилона и Египта. А особенно – землемеры. Еще бы: ведь основа любой цивилизации – распределение угодий и налоги.
Считается, что теоретическая база была доказательно предложена Пифагором в V-м веке до н. э. Хотя, скорее всего, это было сделано ранее.
Теорема Пифагора
Сумма квадратов катетов составляет квадрат гипотенузы:
Верно и обратное утверждение. Треугольник, удовлетворяющий приведенному равенству – прямоугольный.
Формула верна только в Евклидовой геометрии, где параллельные прямые не пересекаются.
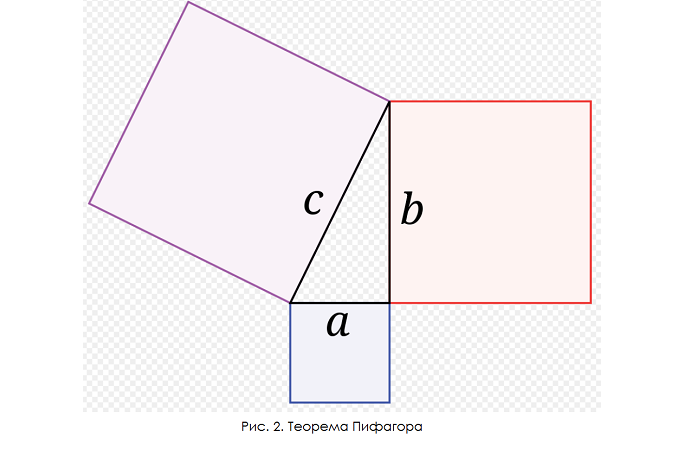
Утверждение приведено в современной интерпретации. В оригинале выглядит несколько по-другому: площадь квадрата, построенного на гипотенузе, идентична сумме площадей квадратов, построенных на катетах (рис. 2).
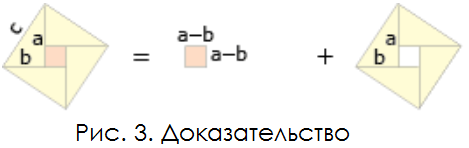
Существует масса способов доказательства. В том числе весьма сложных. А попадаются удивительно изящные, как например, на рисунке 3:
В тригонометрии
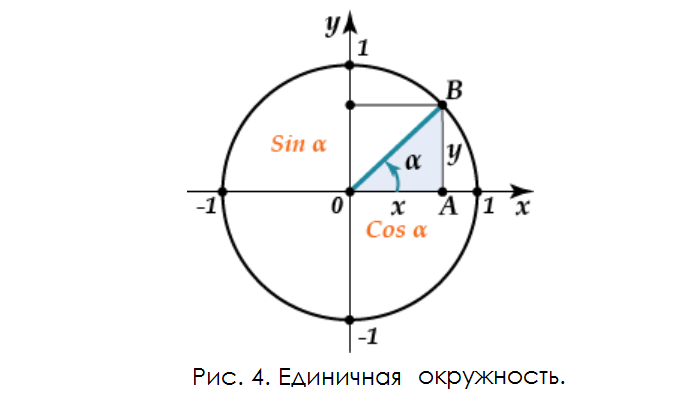
Построим на плоскости прямоугольную систему координат с единичной (с радиусом, равным 1) окружностью с центром в точке (0; 0). B – пересечение угла α и кривой (рис. 4).
На оси абсцисс X отмечается cos α; на оси ординат Y – sin α.
В получившемся прямоугольном треугольнике отрезок 0B является гипотенузой. Учитывая доказанную теорему, выводим основное равенство математической дисциплины:
sin 2 α + cos 2 α = 1
Гипотенуза прямоугольного треугольника
Связана со сторонами следующими соотношениями (см. рис. 1):
a – противолежащий α катет;
Величины sin α и cos α меньше либо равны 1, что очевидно из рис. 4. Но в треугольнике не может быть два прямых угла. Как не может быть нулевого.
Это означает, что гипотенуза – всегда наибольшая сторона треугольника, т. е.
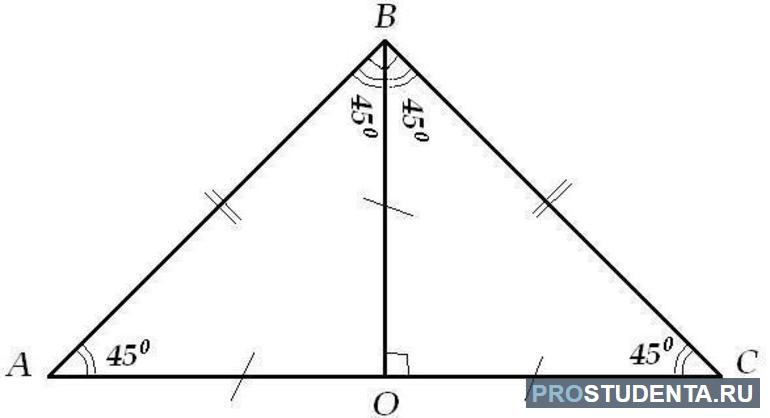
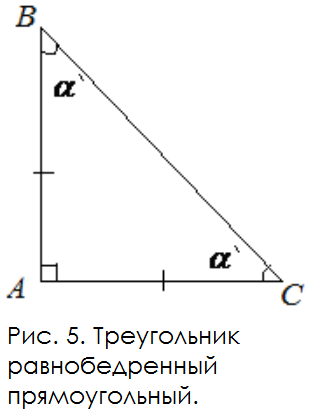
Гипотенуза равнобедренного треугольника
В такой фигуре катеты равны и являются сторонами прямого угла (рис. 5). Расчет гипотенузы c производится по формуле теоремы Пифагора.
Нетрудно заметить, что углы α = 45°. Поскольку сумма всех равна 180°.
Пример решения задачи
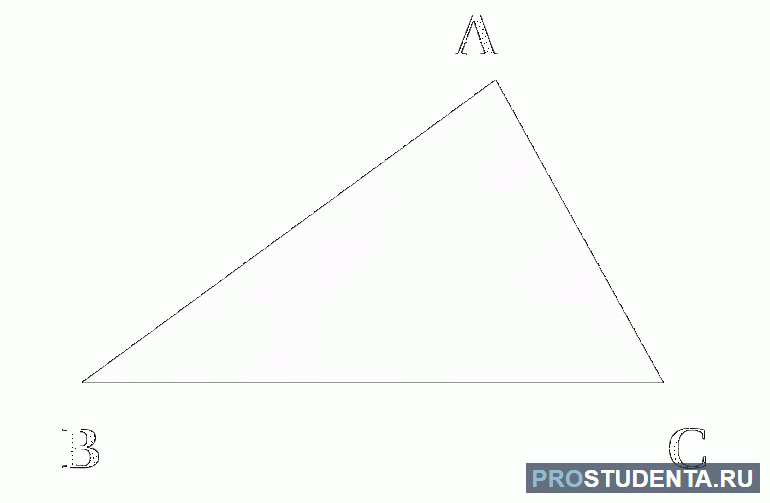
Дан прямоугольный треугольник ABC (рис. 1). Рассчитайте длину AB, если b = 20 см, а β = 70°.
AC является катетом, противолежащим углу β. Значит нахождение гипотенузы сводится к отношениям:
В интернете есть онлайн калькуляторы для оперативного расчета величины. Но целесообразно ими пользоваться разве что при значительном объеме вычислений. Ведь формулы довольно просты.
Связанные с упомянутыми фигурами задачи распространены в реальной жизни. Приведенные уравнения призваны помочь в решении.
Гипотенуза треугольника
Гипотенуза треугольника — это такая сторона треугольника, длина которой равна
квадратному корню из суммы квадратов длин двух других сторон.
Можно сказать, что в треугольнике есть гипотенуза, если длину
какой-нибудь стороны можно выразить по формуле:
Это формула из Теоремы Пифагора. Где с — гипотенуза треугольника, a и b — катеты треугольника.
Не во всех треугольниках есть гипотенуза!
Признаки наличия гипотенузы в треугольнике
Существует ряд случаев / признаков по которым
можно определить, что в треугольнике есть гипотенуза:
Если хотя бы один из вышеперечисленных признаков верен,
соответствует условию задачи, то в треугольнике есть гипотенуза.
Пример гипотенузы в треугольнике
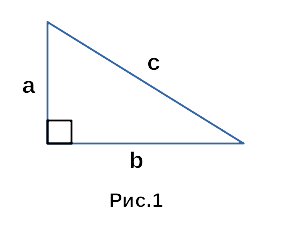
На рисунке 1 изображен прямоугольный треугольник со сторонами a, b, c.
В данном случае, определить какая сторона является гипотенузой
довольно таки просто. Стороны a и b образуют прямой угол,
поэтому сторона c — гипотенуза. Сторона c является гипотенузой
треугольника, так как два смежных с ней угла, образуют в
сумме угол в 90 градусов, т.е прямой.
Длина гипотенузы треугольника
Мы могли бы определить является ли сторона гипотенузой произвольного
треугольника, зная только величину длин всех сторон треугольника.
Как узнать есть ли гипотенуза? Какова её длина?
Допустим, длина стороны a = 3, b = 4, c = 5, тогда по Теореме Пифагора (по признаку гипотенузы в треугольнике):
Все сходится, следовательно гипотенуза в треугольнике есть, и её длина равна 5.
Если в вашем случае ответ не сходится, числа получились в
итоге разные, значит, однозначно гипотенузы в треугольнике нет!
Длину гипотенузы треугольника, можно узнать с помощью Теоремы Пифагора, только в трех базовых случаях:
Гипотенуза
Гипотенуза — сторона в прямоугольном треугольнике, находящаяся напротив прямого угла. Две других стороны — катеты. В прямоугольном треугольнике гипотенуза всегда длиннее катетов.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов (формула: c² = a² + b², где c — гипотенуза, a и b — катеты). Очень часто для вычисления гипотенузы используется именно эта теорема.
Как найти гипотенузу?
Как найти гипотенузу, зная катеты?
Если известны оба катета (две другие стороны прямоугольного треугольника), можно применить Теорему Пифагора.
Теорема Пифагора — в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Формула: c² = a² + b² (при c — гипотенуза, a и b — катеты).
Один катет равен 3 см, другой — 4 см. Таким образом, а = 3, b = 4, подставляем в формулу:
c² = 3² + 4² c² = 9 + 16 c² = 25 c = √25 c = 5.
Ответ: длина гипотенузы 5 см (или x = 5).
Как найти катет в прямоугольном треугольнике
По той же формуле можно найти и длину одного неизвестного катета, нужно только немного её изменить:
Начальная формула: c² = a² + b² (при c — гипотенуза, a и b — катеты), и найти катет можно по этой:
Например: Один катет равен 3 см, а гипотенуза — 5 см. Нужно узнать длину второго катета.
Применяем формулу b = √c² — a² ⇔
b = √5² — 3² ⇔ b = √25 — 9 ⇔ b = √16 ⇔ b = 4.
Как найти гипотенузу, зная катет и угол?
Если есть противолежащий катет — теорема синусов
Если в условии задачи дан угол и противолежащий катет, то ищем гипотенузу по Теореме синусов: стороны треугольника пропорциональны синусам противолежащих углов.
Примечание: гипотенуза есть только в прямоугольном треугольнике, однако теорему синусов можно применять к любым треугольникам (не только к прямоугольным).
Известна одна сторона треугольника 𝐴𝐶 = √2 и ∠β = 45º.
∠α = 90º (т.к. мы ищем гипотенузу, то второй угол в треугольнике прямой, значит имеет 90º).
Так как во всех треугольниках сумма всех углов равна 180º, то можем узнать оставшийся ∠c.
Значит: ∠c = 180º — (90º + 45º) = 45º.
Подставляем в формулу (a/sinα = b/sinβ = c/sinγ) известные:
BC/sin90º = AC/sin45º = AB/sin45º
В таблице вы найдёте значения для синуса:
| sin 45º | √2/2 |
| sin 60º | √3/2 |
| sin 90º | 1 |
В условии задачи нам дано: 𝐴𝐶 = √2, значит:
BC/sin90º = √2/sin45º = AB/sin45º
Подставляем значения синуса из таблицы:
BC/1 = √2/(√2/2) = AB/(√2/2) (забудем на время про катет AB) ⇔
BC = √2/(√2/2) ⇔ BC = 2 (гипотенуза равна 2)
Если хотите вычислить катет, уже зная другой катет и гипотенузу:
Ответ: гипотенуза BC равна 2 см, а катет AB √2 см.
Если есть прилежащий катет — по косинусу
Если в условии задачи дан угол и прилежащий катет, то ищем гипотенузу по косинусу (в прямоугольном треугольнике, косинус острого угла (cos) — это отношение прилежащего катета (b) к гипотенузе(c), таким образом cos a = b/c, из этого получается c = b / cos α).
Т.е. гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α.
Известна одна сторона треугольника AB = 1 и ∠β = 45º. Нужно вычислить гипотенузу (BC).
Помним, что гипотенуза (c) = прилежащий катет (b) / косинус угла или c = b / cos α. Т.е.: BC = AB / cosβ ⇔ BC = 1/ cos 45º.
Смотрим в таблице, чему равен cos 45º.
Ответ: гипотенуза BC равна √2 см.
Как найти гипотенузу равнобедренного треугольника
В равнобедренном треугольнике есть гипотенуза только в том случае, если он одновременно и прямоугольный, т.к. гипотенуза есть только в прямоугольных треугольниках (и его основание будет гипотенузой).
Чтобы найти такую гипотенузу, нужно любой из двух одинаковых катетов возвести в квадрат, умножить на 2 и посчитать квадратный корень: b = √2a² (где b — гипотенуза, а — катет). Это следствие из теоремы Пифагора.
Катет равнобедренного треугольника равен 7см. Нужно найти гипотенузу.
Формула b = √2a². Подставляем:
b = √2*7² = √2*49 ≈ √98 ≈ 9.899
Если забудете эту формулу, можно использовать уже знакомую формулу Пифагора для гипотенузы (c² = a² + b²):