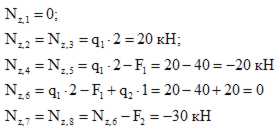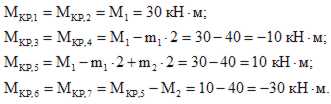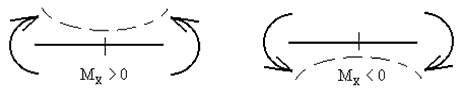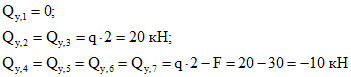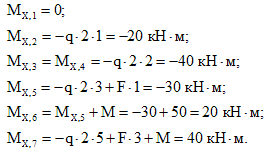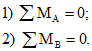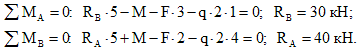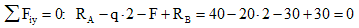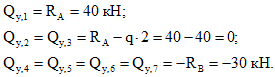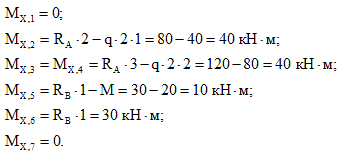Как посчитать эпюру изгибающих моментов

Построение эпюр при изгибе для балки — экспресс курс для чайников

Привет! Вы находитесь на сайте – sopromats.ru, проекте о сопромате и не только! Это новая статья из серии – «сопромат для чайников», в которой я расскажу о построении эпюр при изгибе для балки. Как обычно, буду писать просто и по делу. Здесь я не буду спамить специфическими фразами из сопромата и рассматривать сложные примеры. Будем учиться на простейшей балке. Ну что же давайте начнем учиться!

Сколько можно нарисовать эпюр при изгибе для балок?

Для простого изгиба, который будем рассматривать в этой статье, можно нарисовать всего две эпюры. Одна именуется как эпюра поперечных сил, другая зовется эпюрой изгибающих моментов. Одна показывает распределение внутренних сил внутри элемента, работающего на изгиб, другая моментов. Если хотите, можете изучить больше информации по этим силовым факторам в следующих материалах:

Если Вам лень читать эти статьи, то ничего. Это нормально 🙂 Просто хотел пропиарить немного эти материалы, не зря же я их писал…В этой статье, для чайников, мы, итак, научимся строить эти эпюры, но только одним методом.

Подготовительные работы

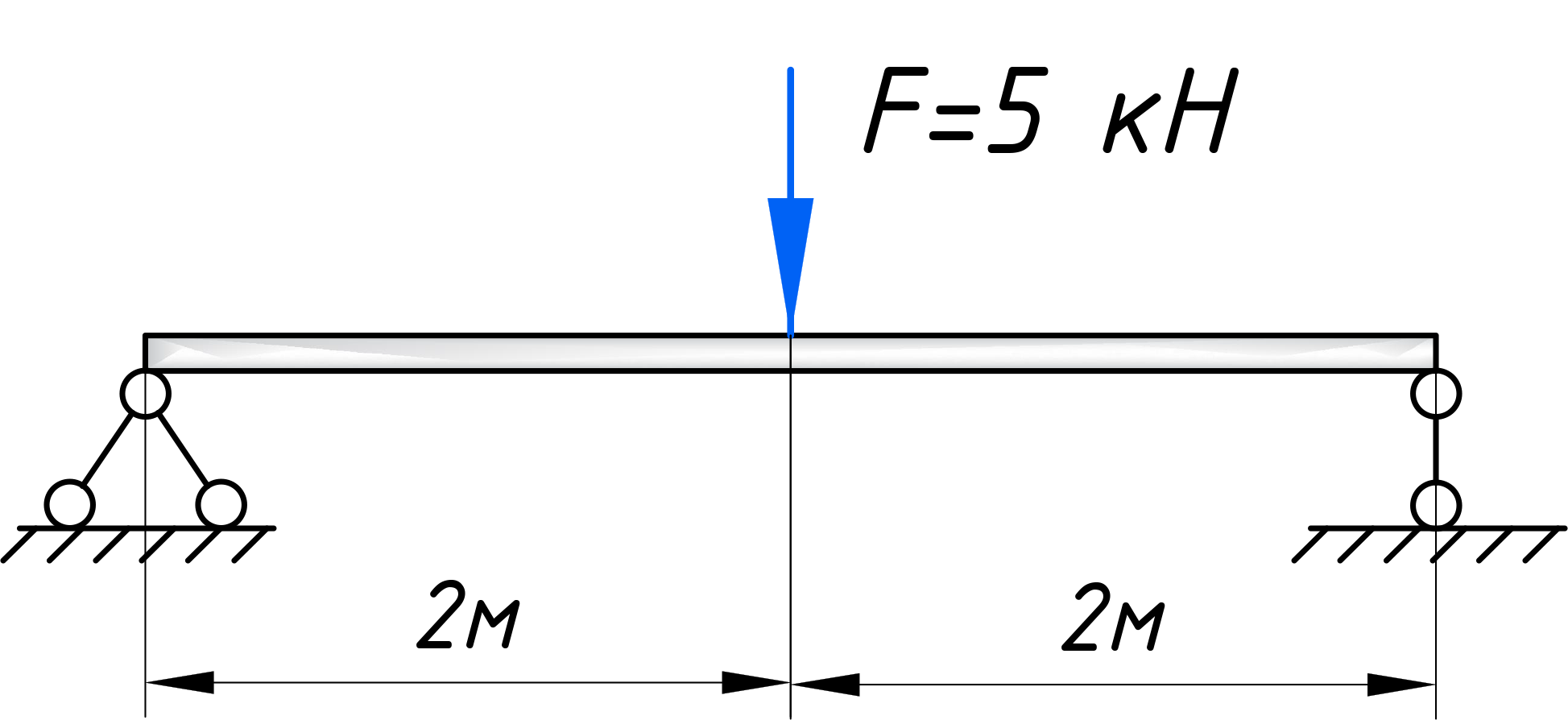
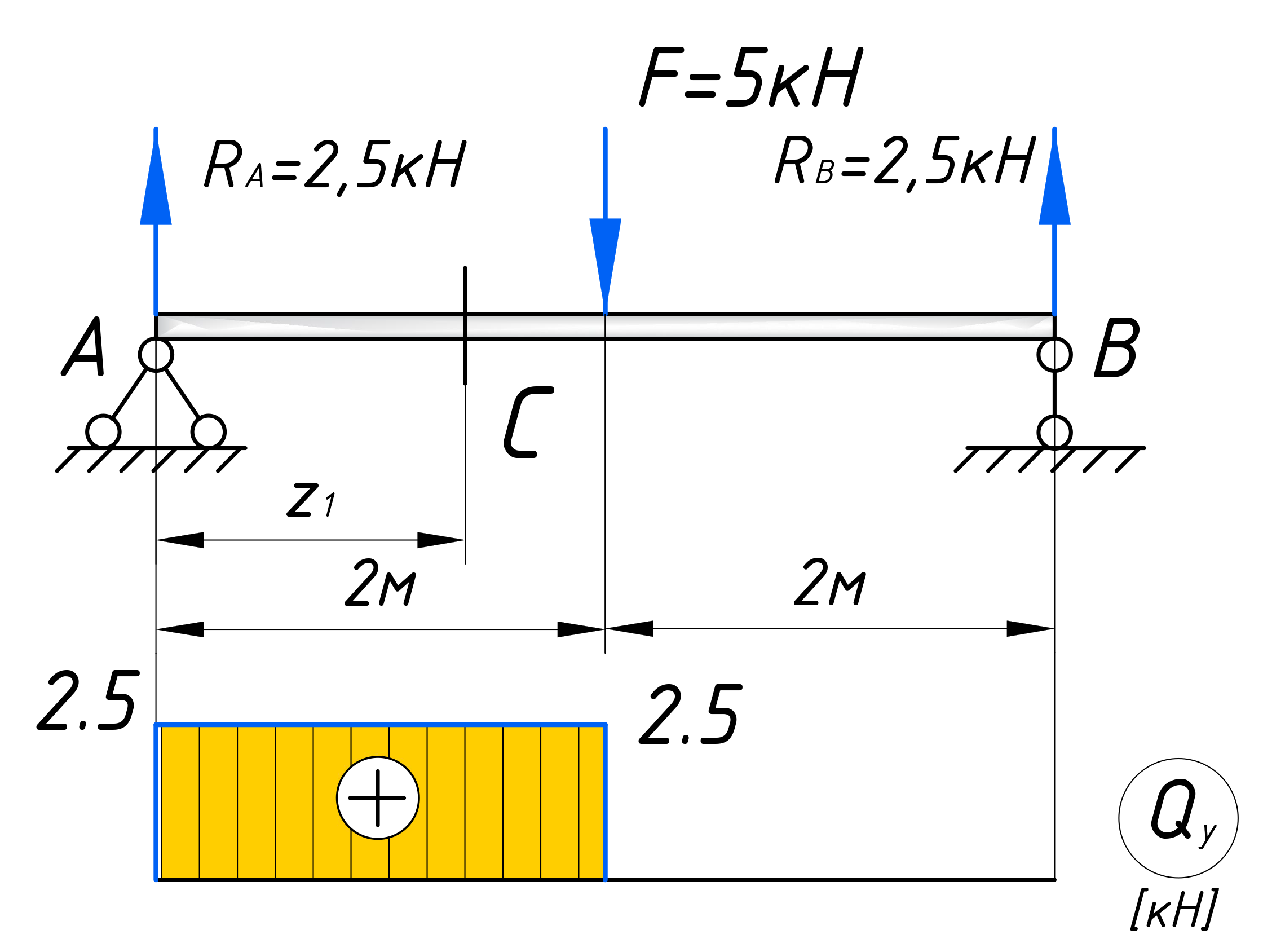
Для того, чтобы построить эпюры, первым делом вычертите расчетную схему, с указанием всех нагрузок и размеров:

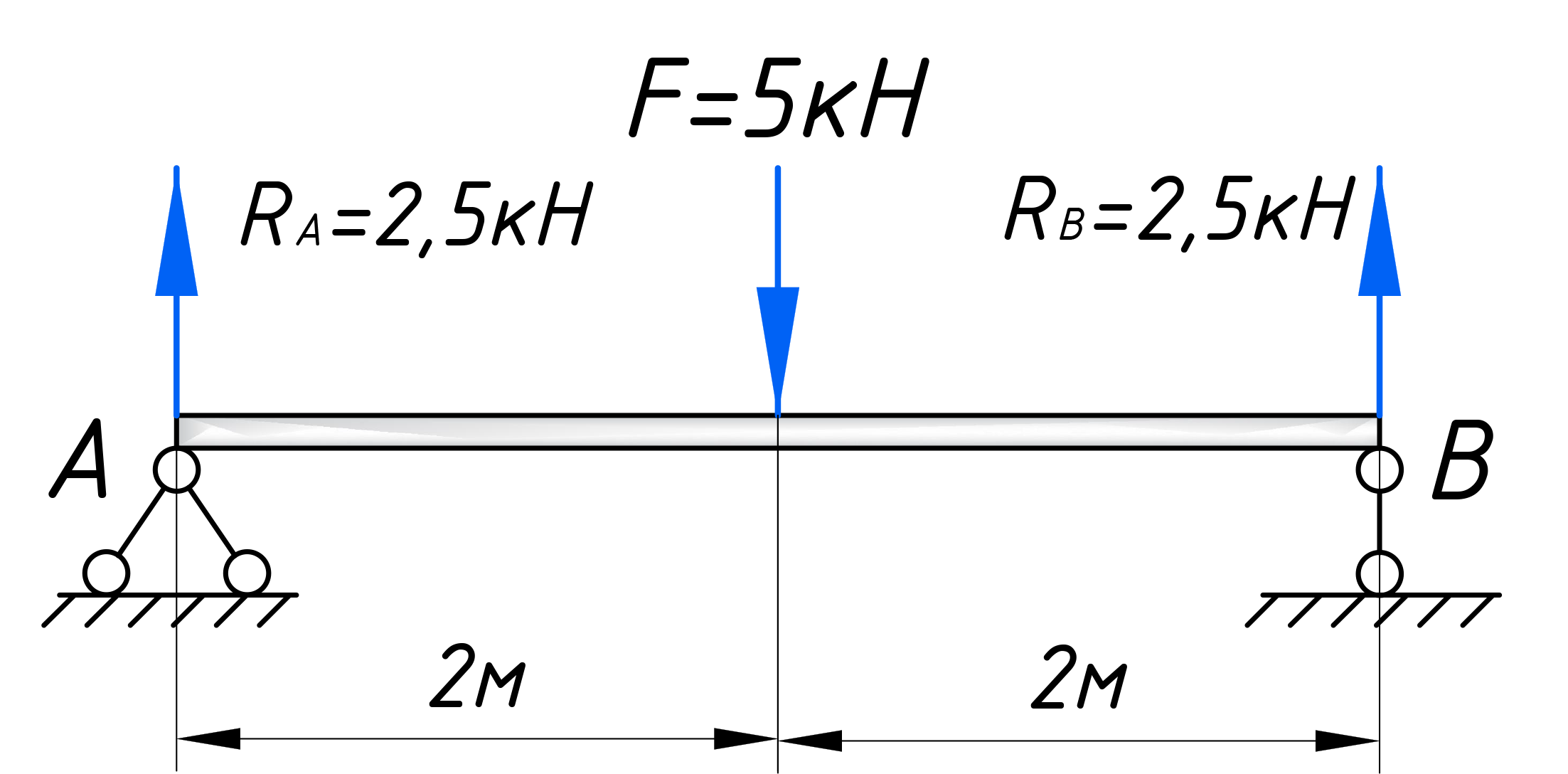
После этого нужно определить реакции опор. Без них дальше никуда. Если Вы не умеет этого делать, обязательно прочтите этот урок про расчет реакций опор для чайников. Здесь же сразу приведу результат вычислений:

Расчет и построение эпюр

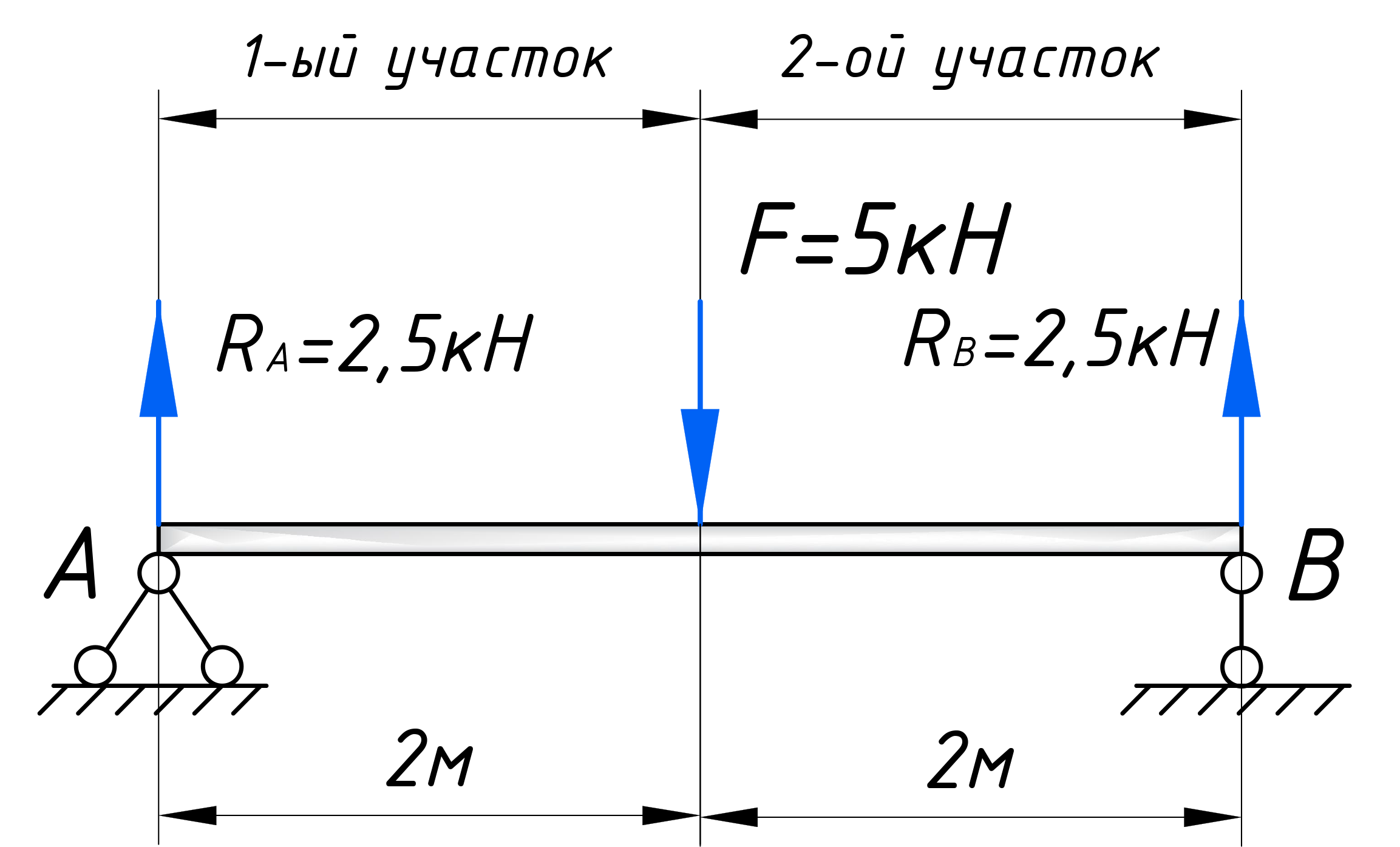
Для расчета эпюр сначала нужно наметить участки, на которых эпюра будет либо постоянна, либо меняться по одному закону. Опознать эти участки достаточно просто. Границами участков служат те места, где прикладываются нагрузки (сосредоточенные силы и моменты, в том числе реакции опор). Если на балку действует распределенная нагрузка, то границы – это ее начало и конец. В нашем случае, как видите, 2 участка, каждый по 2 метра:

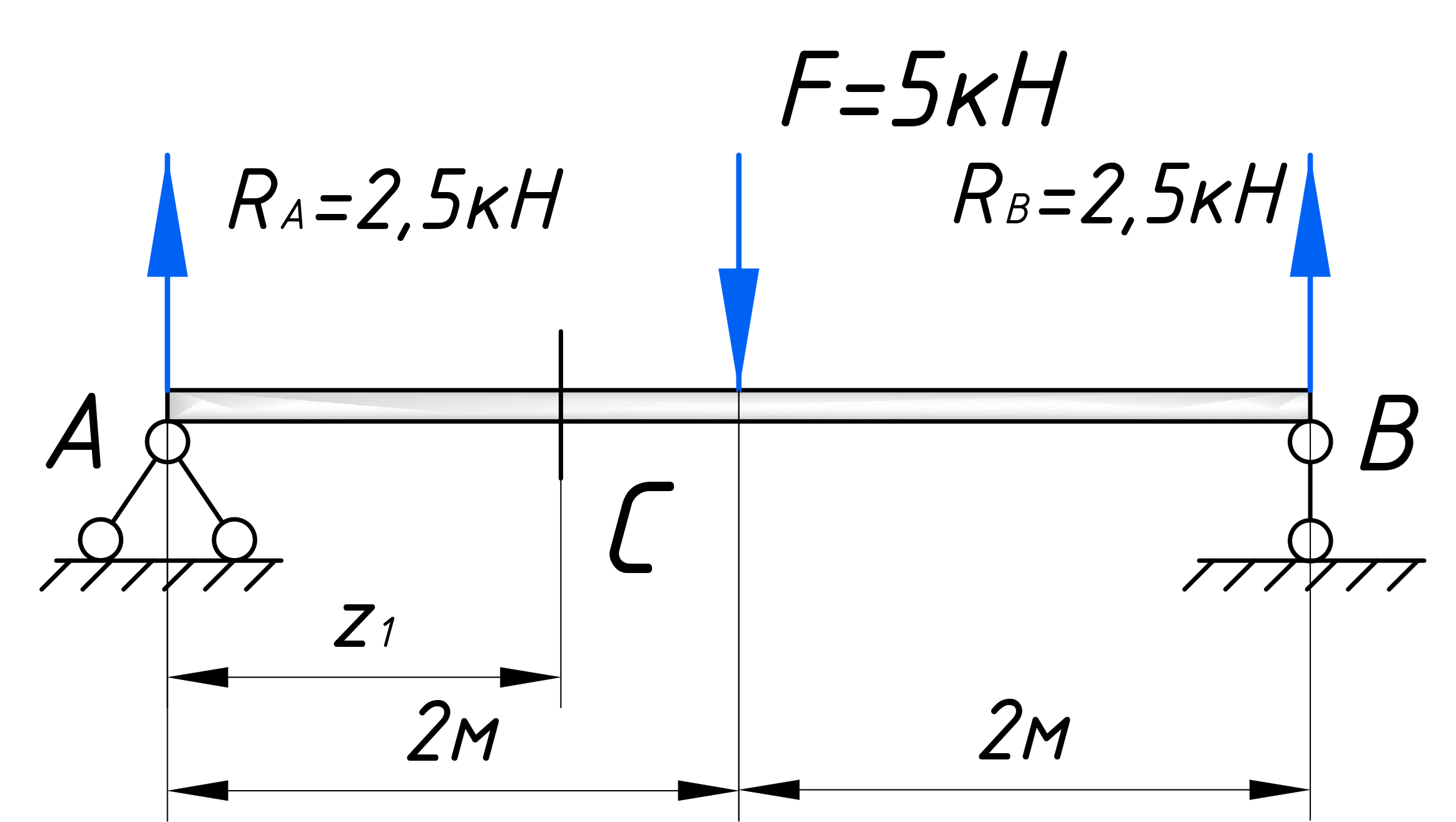
Рассматриваем произвольное сечение первого участка, которое обзовем буквой – С. Оно будет находится на расстоянии z1 от левого торца балки. И относительного него будем записывать законы, по которым меняются поперечные силы и изгибающие моменты на этом участке:

Записываем уравнение для поперечной силы

Поперечная сила будет равняться сумме всех сосредоточенных сил, находящихся слева от сечения (или справа). Мы будем подсчитывать все, что находится слева, т.к. там меньше нагрузки. В уравнении поперечной силы, все внешние нагрузки нужно учитывать с учетом правила знаков: если сила, относительно рассматриваемого сечения, поворачивает ПО часовой стрелке, то в уравнение она пойдет с ПЛЮСОМ (и наоборот).

В рассматриваемом примере, реакция RA поворачивает ПО часовой стрелке, и уравнение получится такое:

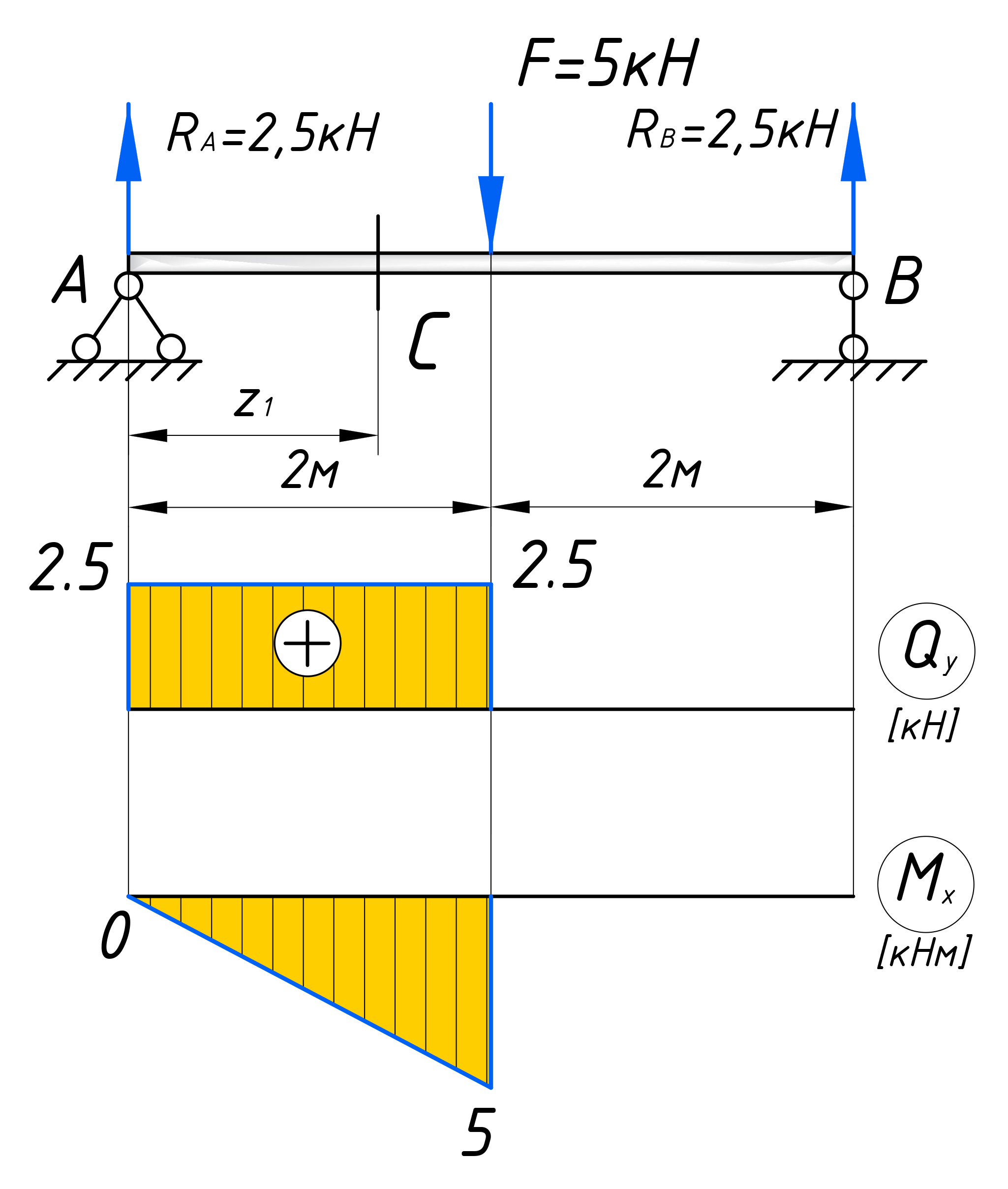
Причем, как видно, эта зависимость справедлива для любого сечения на первом участке, тем самым поперечная сила в пределах этого участка постоянна и равна – 5 кН. Откладываем это значение на графике:

Эпюры заштриховываются перпендикулярно нулевой линии и на каждом участке проставляются знаки поперечной силы.

Записываем уравнение для изгибающего момента

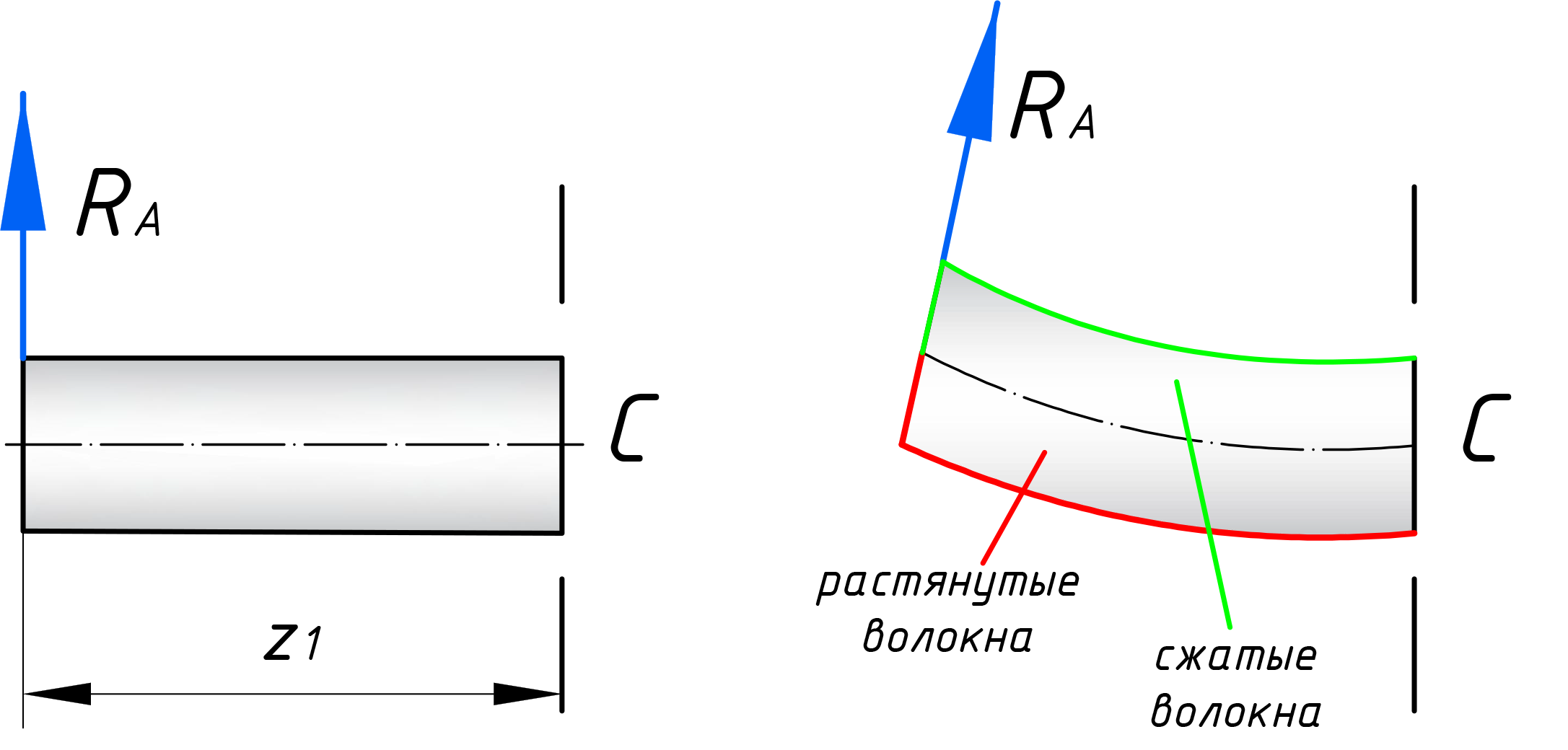
Что касается изгибающего момента, то тут в уравнении нужно учесть сумму моментов, находящихся по одну сторону от сечения. Реакция RA, относительно сечения С создает момент RA·z1. Напомню, что момент – это сила, умноженная на плечо. Где плечо – это расстояние от силы до центра момента (в этом случае, центр – это рассматриваемое сечение). В уравнении моментов, все моменты нужно учитывать с учетом правила знаков: если момент силы, стремится растянуть нижние волокна, то в уравнении будем записывать его со знаком «+». И наоборот.

Придерживаясь этого правила, будем откладывать эпюры изгибающих моментов со стороны РАСТЯНУТЫХ волокон. Что практикуется у инженеров-строителей. У механиков, другие правила, они рисуют эти эпюры со стороны сжатых волокон. Кстати, что такое растянутое и сжатое волокно? Покажу на нашем же примере:

Как видно, сила RA, при повороте, стремится растянуть нижние волокна, поэтому в уравнение будем записывать момент этой силы со знаком плюс:

Анализируя это уравнение, видим, что изгибающий момент будет меняться по линейному закону и зависеть от координаты z1. И чтобы рассчитать и построить эпюру на этом участке достаточно подставить в уравнение координаты начала участка z1=0 и конца z1=2 м. После чего отложить эти точки на графике и соединить прямой линией:

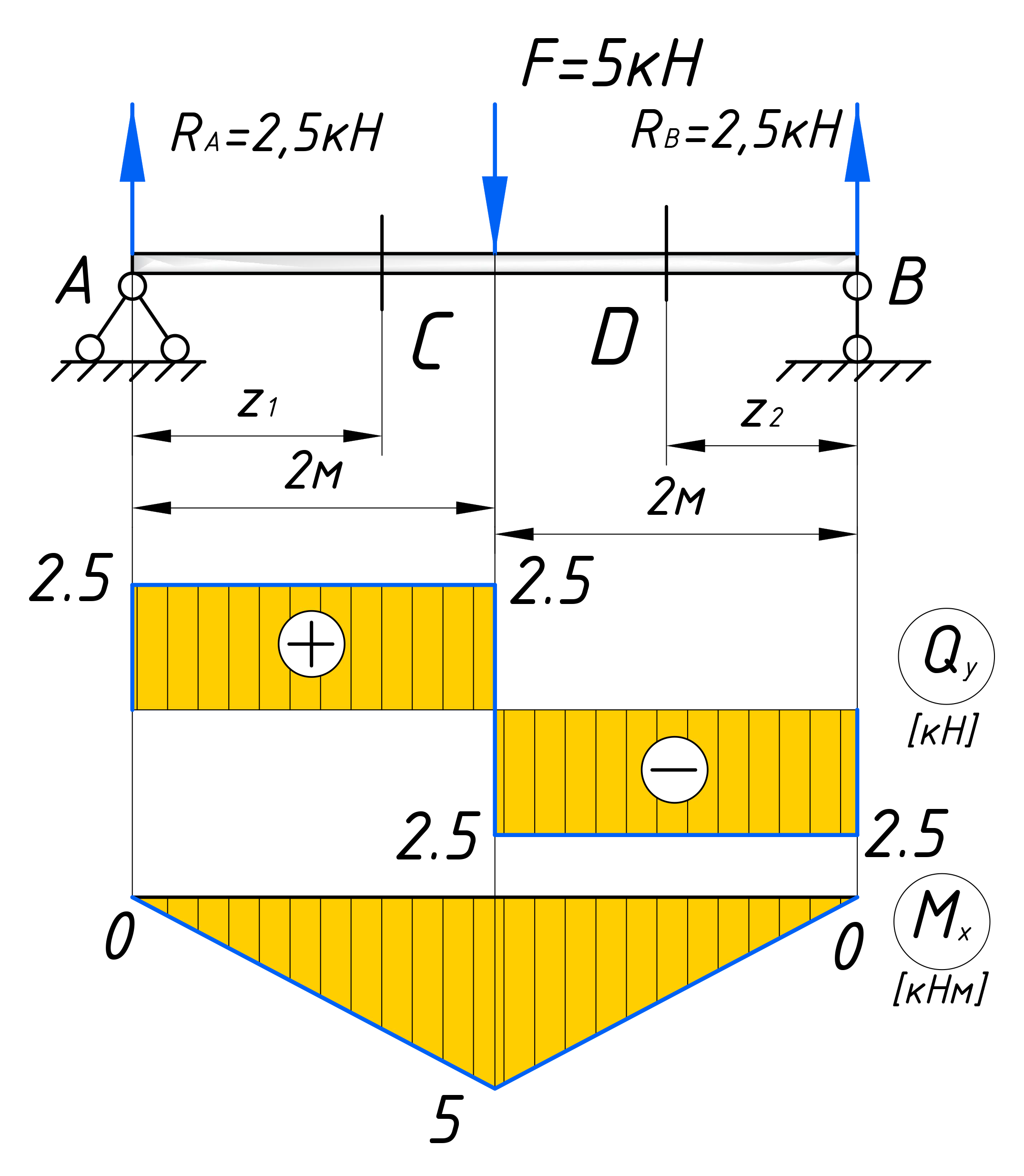
Эпюры для второго участка балки

С учетом всех вышеописанных рекомендаций, я думаю Вы сами теперь сможете построить эпюры для второго участка. Подробно комментировать уже не буду, приведу сразу решение и окончательные эпюры для этой балки:

Сегодня мы рассмотрели урок по построению эпюр для простой балки. Однако, много нюансов по расчету и построению я не рассказал, т.к. все это уместить в одном уроке, довольно сложно и не всем это нужно, статья ведь для чайников! Если Вы хотите прокачать свой знания, в этих вопросах, обязательно прочитайте эти материалы о эпюрах. Здесь можно найти подробные статьи о поперечной силе, о изгибающем моменте. Где я рассказывал о 3-х методиках расчета, причем один из них, даже проще, чем мы рассматривали в данной статье. С помощью которого можно устно рисовать эти эпюры. Также там можно посмотреть, как учитывать моменты и распределенные нагрузки при расчете эпюр и какие особенности есть по построению при действии данных видов нагрузок.

Спасибо за внимание! Если Вам понравилась статья, да и сайт в целом, добавляйте его в свои закладки, чтобы иметь быстрый доступ к нему, а также подписывайтесь на наши соц. сети, делитесь этой статьей с друзьями и т.д. Буду благодарен 🙂

Источник

iSopromat.ru

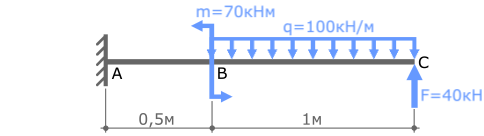
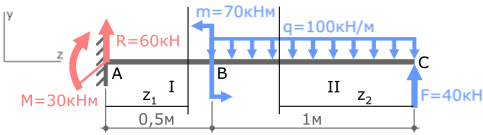
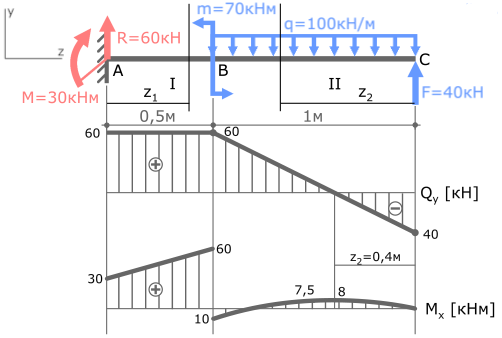
Пример решения задачи на построение эпюры внутренних изгибающих моментов M_x для стальной консольной балки нагруженной сосредоточенной силой F, моментом m и равномерно распределенной нагрузкой q.

Задача

Пример решения

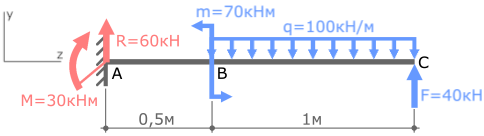
Покажем найденные опорные реакции и выбранную систему координат.

Для построения эпюры изгибающих моментов M_x запишем их выражение по каждому силовому участку и рассчитаем их значения на границах участков. При этом воспользуемся методом сечений.

Наш видеоурок построения эпюр внутренних силовых факторов для балки:

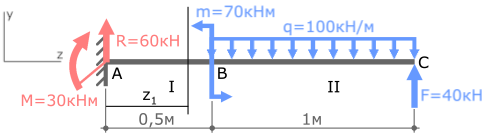
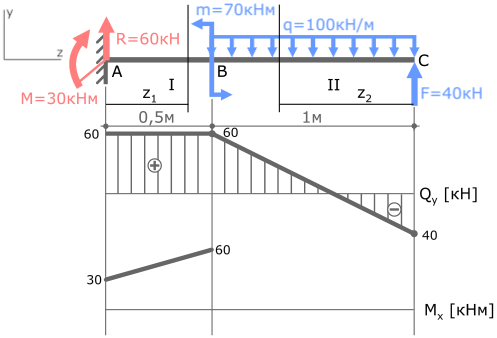
Нумерацию силовых участков балки, сечения и другие вспомогательные обозначения примем из расчета эпюры Q_y.

Рассмотрим I силовой участок:

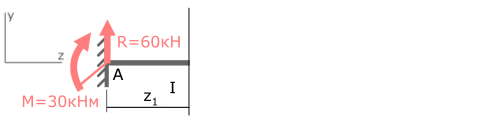
Выбрав левую часть балки, отбросим ненадолго правую, и запишем имеющиеся данные.

Внутренний изгибающий момент в указанном сечении равен сумме всех внешних моментов, воздействующих на рассматриваемую часть балки.

Здесь на момент в рассматриваемом сечении влияют только опорные реакции M и R, то есть сумма моментов состоит из двух слагаемых.

По правилу знаков момент, который стремится сжать верхние слои балки, принимается положительным, следовательно:

В выражении переменная z₁ в первой степени, поэтому эпюра M_x на первом участке будет иметь вид прямой линии.

Рассчитаем значения M_xI на границах участка, т.е. при z₁=0 и при z₁=0,5м

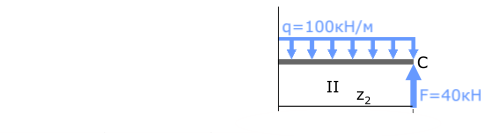
Переходим на второй силовой участок:

Рассекаем балку в произвольном месте участка и рассматриваем её правую часть.

Получено выражение с переменной z₂ во второй степени, значит, эпюра M_x на втором участке будет иметь вид параболы.

Видео про построение эпюр:

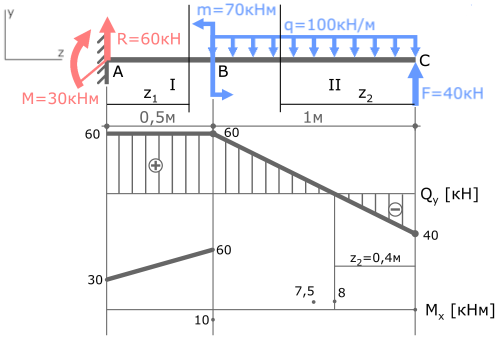
Для построения параболы требуется как минимум три точки. Этими точками будут значения M_x на границах и в середине II силового участка, то есть при z₂=0, z₂=1м и z₂=0,5м.

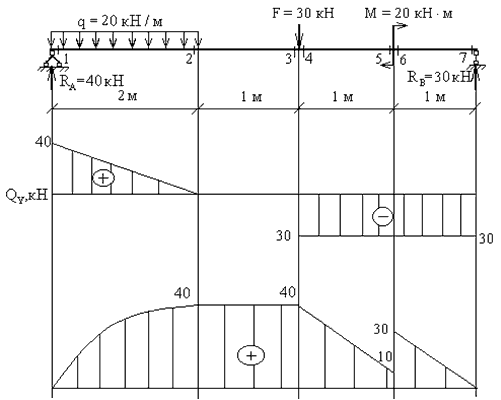
По полученным данным строим эпюру изгибающих моментов M_x (готовую эпюру Q_y перенесем из ранее рассмотренной задачи)

Прежде чем соединять отмеченные точки эпюры параболой, обратите внимание на эпюру поперечных сил Q_y.

Q_y — первая производная от M_x. Поэтому в том месте, где Q_y пересекает базовую линию (т.е. Q_y=0) на эпюре M_x будет экстремум.

Видео про расчет экстремума эпюры:

Рассчитаем значение экстремума эпюры M_x на II участке балки.

Отметив эту точку в области эпюры где Q_y=0 соединим ее с тремя другими параболой.

Эпюра изгибающих моментов построена. Проверка эпюры M_x.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Расчет консольной балки на изгиб пример

Такие вопросы мы сегодня рассмотрим на этой страничке. Здесь есть видео урок на эту тему и описание к ней. Итак, поехали!

Вот какие еще уроки по сопротивлению материалов вы найдете на моем сайте:

Гипотезы и определения при изгибе

Прежде всего начнем с определений и гипотез, которые мы вводим в сопротивлении материалов при изучении изгиба:

Что такое балка? Балка — это стержень, длина которого значительно больше чем ширина и высота. При этом он испытывает деформацию изгиба.

Изгиб, что это? Это такой вид деформации, при котором происходит искривление продольной оси балки, но продольные волокна друг на друга не давят, а сечения плоские до изгиба остаются такими и после изгиба.

На рисунке выше изображена схема для вывода формулы напряжений и демонстрация напряжений, которые возникают при чистом изгибе. Этот термин придется изложить в другой статье. А пока продолжим.

Эпюра — это график изменения величины, для которой он построен. Так эпюра изгибающего момента — это график изменения внутреннего усилия — изгибающего момента по длине балки. Используя этот график, построенный в масштабе, можно с помощь простых операций определить значение изгибающего момента в любой точке по длине балки. Эпюра поперечной силы — аналогично, график ее изменения внутреннего усилия поперечная сила по длине балки.

Построение эпюр при изгибе

Приступим к построению эпюр при изгибе.

Для простоты, возьмем балку защемленную с одной стороны и свободным краем балки с другой стороны (про виды опор и опорные реакции видео урок). Почему так проще? Потому, что при таком способе закрепления не придется определять опорные реакции. Не будет такой необходимости. Дальше будет понятно почему.

На рисунке изображена одна продольная ось, а поперечное сечение не изображается. Что эта за ось? Это та ось, на которой не будет деформаций (нейтральный слой, выше на рисунке). Для сечений, которые простой формы, типа круг, квадрат, прямоугольник, двутавр или сложных составных форм — эта линия всегда проходит через главные центральные оси (опять же пока видео урок «моменты инерции«, а позже статью напишу). Чтобы построить эпюры достаточно и этого.

Итак, со схемой для расчета определились теперь перейдем непосредственно к самому расчету.

Метод сечений при изгибе

Покажем сечение на балке и дадим к нему некоторые пояснения:

Обычно эта схема рисуется одним цветом, но чтобы в тексте было проще описывать — я разделил на три цвета.

Начало координат оси x берем под силой F. Т.е. под этой силой x =0. Положительное направление оси здесь удобно брать влево, в сторону где расположена остальная часть балки. Соответственно x изменяется от нуля до полной длины балки. Только в этих пределах балка существует.

Поэтому x сечения может быть в начале координат, а может быть в конце ну и в промежутке тоже. Нам нужно это понимать, чтобы зависимость для внутренних усилий построить с учетом этого перемещения. Не для конкретного положения сечения, а для любого положения по всей длине балки.

Отсеченную часть рассмотрим отдельно. Запишем условия равновесия для нее. В этом и заключается метод сечений — отсечь, посмотреть на внутренние усилия и найти их из условий равновесия.

На рисунке мы видим отсеченную часть. При этом сам x меняется слева на право от нуля до l.

При таком приложении нагрузки, если других сил на эту часть, кроме силы F, действовать не будет — то этот кусочек балки будет падать вниз, при этом вращаться и перемещаться поступательно. Т.е. совершать плоскопараллельное движение.

Логично предположить, что в реальной конструкции, по сравнению с отсеченной частью что-то эту часть балки «держит», не позволяет «падать». Это и есть силы взаимодействия на межатомном уровне и если их интегрально представлять — внутренние усилия. Значит одно должно удерживать поступательное перемещение вниз, а второе должно удерживать вращательное движение. Поступательное движение вызывает, а значит и может «остановить» — сила, а вращательное — момент. Вот эти усилия нас и интересуют. Внутренние усилия изгибающий момент M(x) и поперечная сила Q(x).

Изобразим их в нашем сечении:

Направление внутренних усилий на рисунке выбрано в соответствии с правилом знаков.

Правило знаков для внутренних усилий при изгибе

А теперь нарисуем, что получилось, немного упростив

Неправда ли, похож на улыбающийся смайлик — это правило знаков для положительного направления изгибающего момента для расчета балки на изгиб. Т.е. любое усилие, вызывающее изгиб балки таким образом, что балка изгибается выпуклостью вниз (веселый смайлик), т.е. растянутые волокна находятся внизу — это будет положительный момент.

Если же смайлик, под действием внешних сил, окажется грустным, как здесь, ниже:

Такие внешние усилия вызывают деформацию изгиба так, что растянутые волокна вверху — это будут изгибающие моменты со знаком минус.

Но пойдем дальше. Ведь наша цель расчет на прочность балки, а не правило знаков при изгибе.

Нами было получено сечение, в котором действуют как внешние, так и внутренние усилия, которые определяют прочность.

Запись аналитических выражений для эпюр внутренних усилий Q(x) и M(x)

Осталось записать внутренние усилия в виде зависимости изгибающего момента М(x) и поперечной силы Q(x). Рисунок, на котором видны эти внутренние усилия мы уже приводили:

Для определения поперечной силы будем использовать сумму проекций на вертикальную ось, а для определения момента возьмем момент относительно точки С.

Так будем всегда поступать при определении изгибающего момента при расчете балки на изгиб. Таким образом мы исключим из этого уравнения момент от Q(x). Связано это с тем, что плечо от Q(x) до точки C равно нулю, потому и момент будет ноль от этой силы.

сумма проекций на вертикальную ось:

Σ Oy: Q(x) — F = 0; ⇒ Q(x) = F;

сумма моментов относительно точки С:

Как видно из окончательных выражений мы получили уравнения для двух прямых линий.

Так как в уравнении моментов координата x входит в первой степени — то это уравнение прямой линии наклоненной к оси x под углом.

Потому первая линия в школе записывалась в виде уравнения:

А вторая записывалась:

На графике же это выглядит так:

Таким образом для построения прямых линий достаточно найти на координатных осях две точки и провести прямые линии под линейку. При построении эпюр моментов и поперечных сил принято брать крайние точки, т.е. точки начала и конца участка этих линий.

Построение эпюр изгибающего момента и поперечной силы при изгибе

Полученные значения изгибающего момента и поперечной силы в двух сечениях (при положении x=0 и x=l) откладываем соответствующие ординаты, т.е. буквально строим графики обеих функций.

Что мы видим из построенных эпюр, какие выводы мы можем сделать:

Когда график начинается не из нуля или не из значения полученного на предыдущем участке, а имеет в одном и том же сечении x два разных значения — такой разрыв функции называется скачок. Т.е. если рассматривать график бесконечно близко слева и бесконечно близко справа мы получаем два разных значения как поперечной силы, так и момента. И этот скачок для поперечной силы должен равняться приложенной сосредоточенной силе, а для момента приложенному сосредоточенному моменту.

Вот и все секреты построения эпюр для моментов и поперечных сил. Конечно дальше немного усложняется сам процесс, но принцип остается тот же.

Дальше в видео представлены примеры построения эпюр для распределенной нагрузки изгибающего момента. Чтобы было проще показать разницу все собрано в одном видео:

Примеры расчета на прочность консольных балок

Для консольных балок рассмотрим три варианта нагрузки и расчета на прочность от каждого из видов нагрузок. Приведу все расчеты в виде рисунков

Источник

Построение эпюр изгибающих моментов и поперечных сил для балок

Автор: Константин Вавилов · Опубликовано 15.08.2015 · Обновлено 16.05.2018

Очень важно уметь строить эпюры для балок, работающих на изгиб! Так как построение эпюр, является неотъемлемой частью любого прочностного расчёта и большинство элементов, из которых состоят современные инженерные сооружения, работают на изгиб. Поэтому в сопромате, очень много внимания уделяется как раз данным эпюрам: поперечных сил и изгибающих моментов. Для краткости, их ещё называют эпюрой моментов и эпюрой сил. В этой статье, рассмотрим, как рассчитать эпюры традиционным методом, а также быстрым, с помощью которого эпюры рисуются за считаные минуты. В статье, построение показано на примере консольной и опирающейся на две опоры балки. Показано, как учитывать сосредоточенные силы и моменты, а также распределённые нагрузки.

Построение эпюр для консольной балки

Первым делом, вводим систему координат, ось x пускаем вдоль оси балки, ось y перпендикулярно ей, а ось z будет перпендикулярна плоскости, в которой размещены две первые оси и будет направлена «к нам».

В поперечных сечениях балки под действием приложенной нагрузки будут возникать два внутренних силовых фактора: поперечная сила и изгибающий момент. Наша задача выяснить, какой величины эти факторы во всех сечениях балки. Для наглядности, результат решения фиксируют в виде так называемых эпюр.

Эпюра строится по всей длине балки, ордината эпюры, под исследуемым сечением, показывает величину внутреннего усилия в этом сечении.

Эпюра поперечных сил

Начнём знакомство с поперечными силами с правила знаков для эпюр. После чего последовательно рассчитаем и построим эпюры для первого и второго участка балки.

Правило знаков для поперечной силы

При построении эпюр поперечных сил нужно придерживаться следующих правил знаков:

Возможно, сейчас будет немного непонятны данные правила, но прочитав следующие 2 блока статьи, вы поймёте, как применять эти правила в действии.

Поперечные силы на первом участке

Рассмотрим первым участок равный двум метрам. Сделаем мысленно сечение на расстоянии x₁ от свободного торца и запишем законы изменения эпюр на этом участке. Законы эти выражаются из уравнений равновесия статики. Статика говорит нам, что тело находится в равновесии, если выполняются следующие условия:

Если суммы проекций всех сил на обе оси равны нулю и сумма моментов относительно точки равна нулю.

Для поперечной силы возьмём сумму проекций на ось y:

Поперечные силы на втором участке

На втором участке, поперечная сила будет равна: Q_{y 2} = Q_{y 1} ;

Так как на этом участке, действует все та же сила F. Момент в уравнениях поперечных сил не учитывается, что является следствием уравнений статики.

Эпюра изгибающих моментов

Правила знаков для изгибающих моментов

То есть, обычно, при построении эпюр изгибающий моментов знаки не указываются. Эти эпюры откладываются со стороны «растянутых волокон». Так, и удобнее читать эпюры и откладывать их.

Не всегда их откладывают так! Студентов некоторых специальностей, чаще всего машиностроительных, учат откладывать эпюры со стороны «сжатых волокон». Строители откладывают со стороны «растянутых волокон», в своих статьях я буду придерживаться этого правила, так как привык к нему.

Изгибающий момент на первом участке

Это закон изменения изгибающих моментов по длине участка. В отличие от поперечных сил, изгибающие моменты будут меняться в пределах этого участка.

Источник

Методика построения эпюр изгибающих моментов, поперечных и продольных сил

1. Виды опорных закреплений

С технической точки зрения опорные закрепления конструкций весьма разнообразны. При решении задач сопромата, все многообразие существующих опорных устройств схематизируется в виде ряда основных типов опор, из которых

наиболее часто встречаются: шарнирно-подвижнаяопора (возможные обозначения для нее представлены на рис.1,а), шарнирно-неподвижная опора (рис.1,б) и жесткое защемление, или заделка (рис.1,в).

В шарнирно-подвижной опоре возникает одна опорная реакция, перпендикулярная опорной плоскости. Такая опора лишает опорное сечение одной степени свободы, то есть препятствует смещению в направлении опорной плоскости, но допускает перемещение в перпендикулярном направлении и поворот опорного сечения.
В шарнирно-неподвижной опоре возникают вертикальная и горизонтальная реакции. Здесь невозможны перемещения по направлениям опорных стержней, но допускается поворот опорного сечения.
В жесткой заделке возникают вертикальная и горизонтальная реакции и опорный (реактивный) момент. При этом опорное сечение не может смещаться и поворачиваться.При расчете систем, содержащих жесткую заделку, возникающие опорные реакции можно не определять, выбирая при этом отсеченную часть так, чтобы заделка с неизвестными реакциями в нее не попадала. При расчете систем на шарнирных опорах реакции опор должны быть определены обязательно. Уравнения статики, используемые для этого, зависят от вида системы (балка, рама и др.) и будут приведены в соответствующих разделах настоящего пособия.

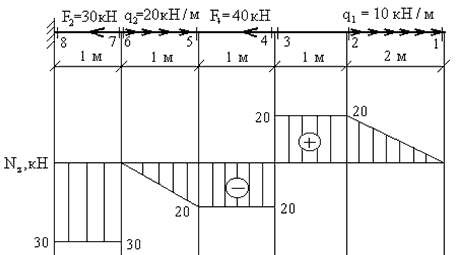
2. Построение эпюр продольных сил N z

Продольная сила в сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня.

Пример 1.Построить эпюру продольных сил для жестко защемленной балки (рис.2).

1. Намечаем характерные сечения, нумеруя их от свободного конца стержня к заделке.
2. Определяем продольную силу Nz в каждом характерном сечении. При этом рассматриваем всегда ту отсеченную часть, в которую не попадает жесткая заделка.

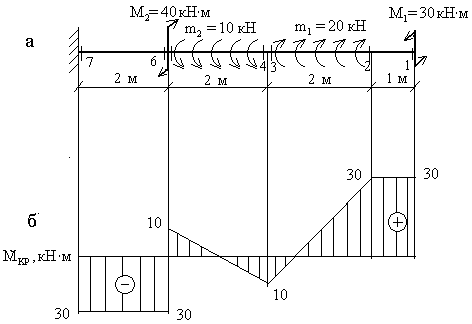
Крутящий момент в сечении численно равен алгебраической сумме внешних моментов, приложенных по одну сторону от рассматриваемого сечения, относительно продольной оси Z.

Пример 2.Построить эпюру крутящих моментов для жестко защемленного стержня (рис.3,а).

Следует отметить, что алгоритм и принципы построения эпюры крутящих моментов полностью совпадают с алгоритмом и принципами построения эпюры продольных сил.

1.Намечаем характерные сечения.
2.Определяем крутящий момент в каждом характерном сечении.

По найденным значениям строимэпюру Мкр (рис.3,б).

Для эпюр продольных сил и крутящих моментов характерны определенные закономерности, знание которых позволяет оценить правильность выполненных построений.

1. Эпюры Nz и Мкр всегда прямолинейные.

3. Под точкой приложения сосредоточенной силы на эпюре Nz обязательно должен быть скачок на величину этой силы, аналогично под точкой приложения сосредоточенного момента на эпюре Мкр будет скачок на величину этого момента.

5. Построение эпюр поперечных сил Q y и изгибающих моментов M x в балках

Поперечная сила в сечении численно равна алгебраической сумме проекций внешних сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную (вертикальную) ось.

Схематически это правило знаков можно представить в виде

Схематически это правило знаков можно представить в виде:

Следует отметить, что при использовании правила знаков для Mx в указанном виде, эпюра Mx всегда оказывается построенной со стороны сжатых волокон балки.

6. Консольные балки

При построении эпюр Qy и Mx в консольных, или жестко защемленных, балках нет необходимости (как и в рассмотренных ранее примерах) вычислять опорные реакции, возникающие в жесткой заделке, но выбирать отсеченную часть нужно так, чтобы заделка в нее не попадала.

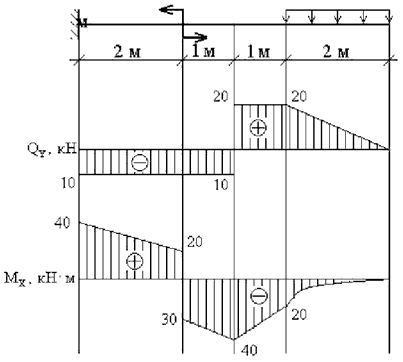
Пример 3.Построить эпюры Qy и Mx (рис.4).

1. Намечаем характерные сечения.

2. Определяем поперечную силу Qy в каждом характерном сечении.

По вычисленным значениям строим эпюру Qy.

3. Определяем изгибающий момент Mx в каждом характерном сечении.

По вычисленным значениям строим эпюру Mx, причем, на участке под распределенной нагрузкой эпюра будет криволинейной (квадратная парабола). Выпуклость кривой на этом участке всегда обращена навстречу распределенной нагрузке.

7. Балки на двух опорах

В отличие от консольных балок, при расчете балок на двух шарнирных опорах необходимо сначала определить опорные реакции из уравнений статики, так как и в левую, и в правую отсеченные части для любого сечения, расположенного между опорами, попадает соответствующая реакция.

Для плоской системы число уравнений статики в общем случае равно трем. Если балка загружена только вертикальными нагрузками, то горизонтальная реакция шарнирно-неподвижной опоры равна нулю, и одно из уравнений равновесия обращается в тождество. Таким образом, для определения реакций в опорах шарнирной балки используются два уравнения статики:

Пример 4. Построить эпюры Qy, Mx для балки с шарнирным опиранием (рис.5).

1. Вычисляем реакции опор.

2. Намечаем характерные сечения.

В отличие от консольных балок здесь известны обе опорные реакции, поэтому для любого сечения можно рассматривать как левую, так и правую отсеченную часть.

3. Определяем поперечные силы в характерных сечениях.

4. Определяем изгибающие моменты в характерных сечениях.

8. Правила контроля эпюр Q у и M x

Дифференциальные зависимости между q, Qy, Mx определяют ряд закономерностей, которым подчиняются эпюры Qy и Mx.

Под точкой приложения сосредоточенной силы (реакции) на эпюре Qy обязательно должен быть скачок на величину этой силы (реакции). Аналогично, под точкой приложения сосредоточенного момента на эпюре Mx обязателен скачок на величину момента.

Если на участке под распределенной нагрузкой эпюра Qy пересекает ось (Qy=0), то эпюра Mx в этом сечении имеет экстремум.

На участках с поперечной силой одного знака эпюра Mx имеет одинаковую монотонность. Так, при Qy>0 эпюра Mx возрастает слева направо; при Qy

Источник