Как посчитать достоверность различий p

Критерий Стьюдента в Microsoft Excel

Одним из наиболее известных статистических инструментов является критерий Стьюдента. Он используется для измерения статистической значимости различных парных величин. Microsoft Excel обладает специальной функцией для расчета данного показателя. Давайте узнаем, как рассчитать критерий Стьюдента в Экселе.

Определение термина

Но, для начала давайте все-таки выясним, что представляет собой критерий Стьюдента в общем. Данный показатель применяется для проверки равенства средних значений двух выборок. То есть, он определяет достоверность различий между двумя группами данных. При этом, для определения этого критерия используется целый набор методов. Показатель можно рассчитывать с учетом одностороннего или двухстороннего распределения.

Расчет показателя в Excel

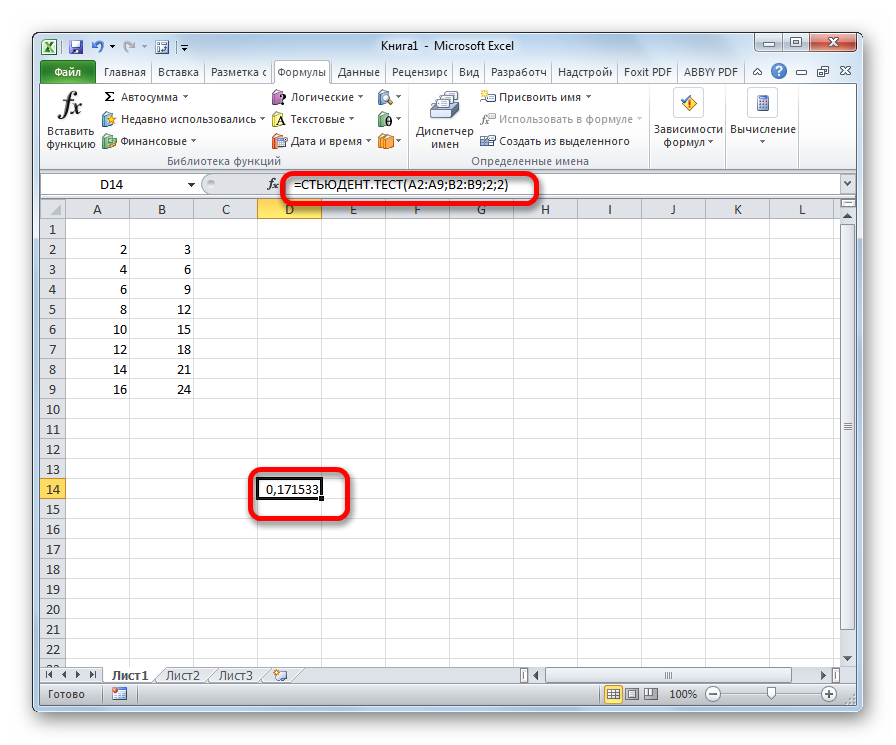
Теперь перейдем непосредственно к вопросу, как рассчитать данный показатель в Экселе. Его можно произвести через функцию СТЬЮДЕНТ.ТЕСТ. В версиях Excel 2007 года и ранее она называлась ТТЕСТ. Впрочем, она была оставлена и в позднейших версиях в целях совместимости, но в них все-таки рекомендуется использовать более современную — СТЬЮДЕНТ.ТЕСТ. Данную функцию можно использовать тремя способами, о которых подробно пойдет речь ниже.

Способ 1: Мастер функций

Проще всего производить вычисления данного показателя через Мастер функций.

В поле «Хвосты» вписываем значение «1», если будет производиться расчет методом одностороннего распределения, и «2» в случае двухстороннего распределения.

В поле «Тип» вводятся следующие значения:

Когда все данные заполнены, жмем на кнопку «OK».

Выполняется расчет, а результат выводится на экран в заранее выделенную ячейку.

Способ 2: работа со вкладкой «Формулы»

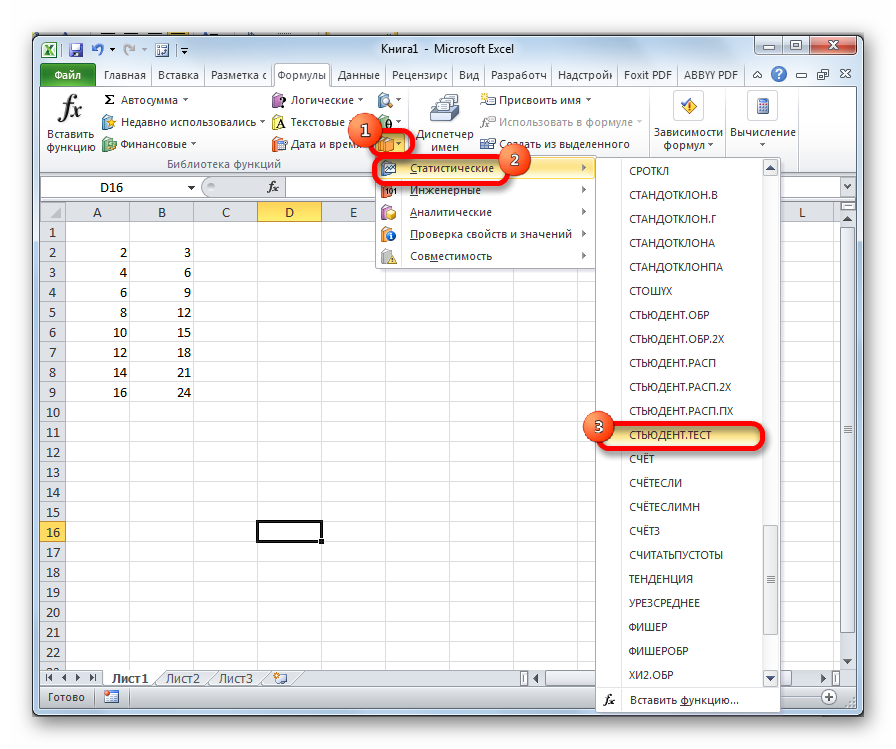
Функцию СТЬЮДЕНТ.ТЕСТ можно вызвать также путем перехода во вкладку «Формулы» с помощью специальной кнопки на ленте.

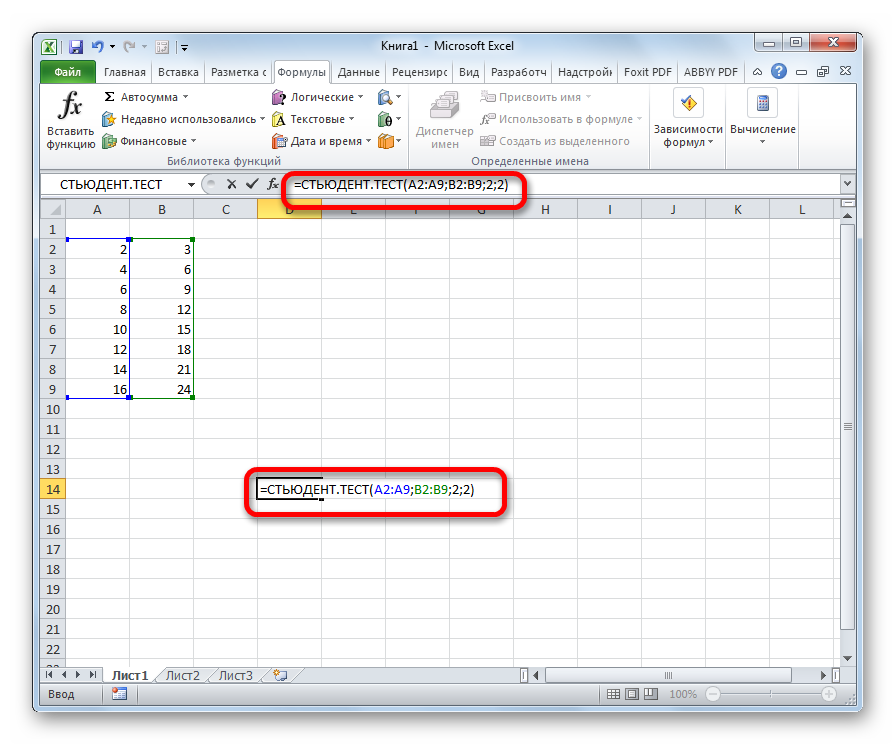
Способ 3: ручной ввод

Формулу СТЬЮДЕНТ.ТЕСТ также можно ввести вручную в любую ячейку на листе или в строку функций. Её синтаксический вид выглядит следующим образом:

Что означает каждый из аргументов, было рассмотрено при разборе первого способа. Эти значения и следует подставлять в данную функцию.

После того, как данные введены, жмем кнопку Enter для вывода результата на экран.

Как видим, вычисляется критерий Стьюдента в Excel очень просто и быстро. Главное, пользователь, который проводит вычисления, должен понимать, что он собой представляет и какие вводимые данные за что отвечают. Непосредственный расчет программа выполняет сама.

Помимо этой статьи, на сайте еще 12538 инструкций.
Добавьте сайт Lumpics.ru в закладки (CTRL+D) и мы точно еще пригодимся вам.

Отблагодарите автора, поделитесь статьей в социальных сетях.

Источник

Что такое p-value?

P-значение (англ. P-value) — величина, используемая при тестировании статистических гипотез. Фактически это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода). Проверка гипотез с помощью P-значения является альтернативой классической процедуре проверки через критическое значение распределения.

Обычно P-значение равно вероятности того, что случайная величина с данным распределением (распределением тестовой статистики при нулевой гипотезе) примет значение, не меньшее, чем фактическое значение тестовой статистики. Википедия.

Иначе говоря, p-значение – это наименьшее значение уровня значимости (т.е. вероятности отказа от справедливой гипотезы), для которого вычисленная проверочная статистика ведет к отказу от нулевой гипотезы. Обычно p-значение сравнивают с общепринятыми стандартными уровнями значимости 0,005 или 0,01.

Например, если вычисленное по выборке значение проверочной статистики соответствует p = 0,005, это указывает на вероятность справедливости гипотезы 0,5%. Таким образом, чем p-значение меньше, тем лучше, поскольку при этом увеличивается «сила» отклонения нулевой гипотезы и увеличивается ожидаемая значимость результата.

Интересное объяснение этого есть на Хабре.

Статистический анализ начинает напоминать черный ящик: на вход подаются данные, на выход — таблица основных результатов и значение p-уровня значимости (p-value).

О чём говорит p-value?

Предположим, мы решили выяснить, существует ли взаимосвязь между пристрастием к кровавым компьютерным играм и агрессивностью в реальной жизни. Для этого были случайным образом сформированы две группы школьников по 100 человек в каждой (1 группа — фанаты стрелялок, вторая группа — не играющие в компьютерные игры). В качестве показателя агрессивности выступает, например, число драк со сверстниками. В нашем воображаемом исследовании оказалось, что группа школьников-игроманов действительно заметно чаще конфликтует с товарищами. Но как нам выяснить, насколько статистически достоверны полученные различия? Может быть, мы получили наблюдаемую разницу совершенно случайно? Для ответа на эти вопросы и используется значение p-уровня значимости (p-value) — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет. Иными словами, это вероятность получить такие или еще более сильные различия между нашими группами, при условии, что, на самом деле, компьютерные игры никак не влияют на агрессивность. Звучит не так уж и сложно. Однако, именно этот статистический показатель очень часто интерпретируется неправильно.

Примеры про p-value

Итак, мы сравнили две группы школьников между собой по уровню агрессивности при помощи стандартного t-теста (или непараметрического критерия Хи — квадрат более уместного в данной ситуации) и получили, что заветный p-уровень значимости меньше 0.05 (например 0.04). Но о чем в действительности говорит нам полученное значение p-уровня значимости? Итак, если p-value — это вероятность получить такие или более выраженные различия при условии, что в генеральной совокупности никаких различий на самом деле нет, то какое, на ваш взгляд, верное утверждение:

1.Компьютерные игры — причина агрессивного поведения с вероятностью 96%.
2. Вероятность того, что агрессивность и компьютерные игры не связаны, равна 0.04.
3. Если бы мы получили p-уровень значимости больше, чем 0.05, это означало бы, что агрессивность и компьютерные игры никак не связаны между собой.
4. Вероятность случайно получить такие различия равняется 0.04.
5. Все утверждения неверны.

Если вы выбрали пятый вариант, то абсолютно правы! Но, как показывают многочисленные исследования, даже люди со значительным опытом в анализе данных часто некорректно интерпретируют значение p-value.

Давайте разберём все ответы по порядку:

Первое утверждение — пример ошибки корреляции: факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Может быть, это более агрессивные люди предпочитают проводить время за компьютерными играми, а вовсе не компьютерные игры делают людей агрессивнее.

Это уже более интересное утверждение. Всё дело в том, что мы изначально принимаем за данное, что никаких различий на самом деле нет. И, держа это в уме как факт, рассчитываем значение p-value. Поэтому правильная интерпретация: «Если предположить, что агрессивность и компьютерные игры никак не связаны, то вероятность получить такие или еще более выраженные различия составила 0.04».

А что делать, если мы получили незначимые различия? Значит ли это, что никакой связи между исследуемыми переменными нет? Нет, это означает лишь то, что различия, может быть, и есть, но наши результаты не позволили их обнаружить.

Это напрямую связано с самим определением p-value. 0.04 — это вероятность получить такие или ещё более экстремальные различия. Оценить вероятность получить именно такие различия, как в нашем эксперименте, в принципе невозможно!

Вот такие подводные камни могут скрываться в интерпретации такого показателя, как p-value. Поэтому очень важно понимать механизмы, заложенные в основании методов анализа и расчета основных статистических показателей.

Как найти p-value?

1. Определите ожидаемые в вашем эксперименте результаты

Обычно когда ученые проводят эксперимент, у них уже есть идея того, какие результаты считать «нормальными» или «типичными». Это может быть основано на экспериментальных результатах прошлых опытов, на достоверных наборах данных, на данных из научной литературы, либо ученый может основываться на каких-либо других источниках. Для вашего эксперимента определите ожидаемые результаты, и выразите их в виде чисел.

Пример: Например, более ранние исследования показали, что в вашей стране красные машины чаще получают штрафы за превышение скорости, чем синие машины. Например, средние результаты показывают предпочтение 2:1 красных машин перед синими. Мы хотим определить, относится ли полиция точно так же предвзято к цвету машин в вашем городе. Для этого мы будем анализировать штрафы, выданные за превышение скорости. Если мы возьмем случайный набор из 150 штрафов за превышение скорости, выданных либо красным, либо синим автомобилям, мы ожидаем, что 100 штрафов будет выписано красным автомобилям, а 50 синим, если полиция в нашем городе так же предвзято относится к цвету машин, как это наблюдается по всей стране.

2. Определите наблюдаемые результаты вашего эксперимента

Теперь, когда вы опредили ожидаемые результаты, необходимо провести эксперимент, и найти действительные (или «наблюдаемые») значения. Вам снова необходимо представить эти результаты в виде чисел. Если мы создаем экспериментальные условия, и наблюдаемые результаты отличаются от ожидаемых, то у нас есть две возможности – либо это произошло случайно, либо это вызвано именно нашим экспериментом. Цель нахождения p-значения как раз и состоит в том, чтобы определить, отличаются ли наблюдаемые результаты от ожидаемых настолько, чтобы можно было не отвергать «нулевую гипотезу» – гипотезу о том, что между экспериментальными переменными и наблюдаемыми результатами нет никакой связи.

Пример: Например, в нашем городе мы случайно выбрали 150 штрафов за превышение скорости, которые были выданы либо красным, либо синим автомобилям. Мы определили, что 90 штрафов были выписаны красным автомобилям, и 60 синим. Это отличается от ожидаемых результатов, которые равны 100 и 50, соответственно. Действительно ли наш эксперимент (в данном случае, изменение источника данных с национального на городской) привел к данному изменению в результатах, или наша городская полиция относится предвзято точно так же, как и в среднем по стране, а мы видим просто случайное отклонение? P-значение поможет нам это определить.

3. Определите число степеней свободы вашего эксперимента

Число степеней свободы — это степень изменяемости вашего эксперимента, которая определяется числом категорий, которые вы исследуете. Уравнение для числа степеней свободы – Число степеней свободы = n-1, где «n» это число категорий или переменных, которые вы анализируете в своем эксперименте.

Пример: В нашем эксперименте две категории результатов: одна категория для красных машин, и одна для синих машин. Поэтому в нашем эксперименте у нас 2-1 = 1 степень свободы. Если бы мы сравнивали красные, синие и зеленые машины, у нас было бы 2 степени свободы, и так далее.

4. Сравните ожидаемые и наблюдаемые результаты с помощью критерия хи-квадрат

Хи-квадрат (пишется «x2») это числовое значение, которое измеряет разницу между ожидаемыми и наблюдаемыми значениями эксперимента. Уравнение для хи-квадрата следующее x2 = Σ((o-e)2/e), где «o» это наблюдаемое значение, а «e» это ожидаемое значение. Суммируйте результаты данного уравнения для всех возможных результатов (смотри ниже).

Заметьте, что данное уравнение включает оператор суммирования Σ (сигма). Другими словами, вам необходимо подсчитать ((|o-e|-.05)2/e) для каждого возможного результата, и сложить полученные числа, чтобы получить значение критерия хи-квадрат. В нашем примере у нас два возможных результата – либо машина, получившая штраф красная, либо синяя. Поэтому мы должны посчитать ((o-e)2/e) дважды – один раз для красных машин, и один раз для синих машин.

Пример: Давайте подставим наши ожидаемые и наблюдаемые значения в уравнение x2 = Σ((o-e)2/e). Помните, что из-за оператора суммирования нам необходимо посчитать ((o-e)2/e) дважды – один раз для красных автомобилей, и один раз для синих автомобилей. Мы выполним эту работу следующим образом:
x2 = ((90-100)2/100) + (60-50)2/50)
x2 = ((-10)2/100) + (10)2/50)
x2 = (100/100) + (100/50) = 1 + 2 = 3.

5. Выберите уровень значимости

Теперь, когда мы знаем число степеней свободы нашего эксперимента, и узнали значение критерия хи-квадрат, нам нужно сделать еще одну вещь перед тем, как мы найдем наше p-значение. Нам нужно определить уровень значимости. Говоря простым языком, уровень значимости показывает, насколько мы уверены в наших результатах. Низкое значение для значимости соответствует низкой вероятности того, что экспериментальные результаты получились случайно, и наоборот. Уровни значимости записываются в виде десятичных дробей (таких как 0.01), что соответствует вероятности того, что экспериментальные результаты мы получили случайно (в данном случае вероятность этого 1%).

По соглашению, ученые обычно устанавливают уровень значимости своих экспериментов равным 0.05, или 5%.[2] Это означает, что экспериментальные результаты, которые соответствуют такому критерию значимости, только с вероятностью 5% могли получиться чисто случайно. Другими словами, существует 95% вероятность, что результаты были вызваны тем, как ученый манипулировал экспериментальными переменными, а не случайно. Для большинства экспериментов 95% уверенности наличия связи между двумя переменными достаточно, чтобы считать, что они «действительно» связаны друг с другом.

Пример: для нашего примера с красными и синими машинами, давайте последуем соглашению между учеными, и установим уровень значимости в 0.05.

6. Используйте таблицу с данными распределения хи-квадрат, чтобы найти ваше p-значение

Ученые и статисты используют большие таблицы для вычисления p-значения своих экспериментов. Данные таблицы обычно имеют вертикальную ось слева, соответствующую числу степеней свободы, и горизонтальную ось сверху, соответствующую p-значению. Используйте данные таблицы, чтобы сначала найти число ваших степеней свободы, затем посмотрите на ваш ряд слева направо, пока не найдете первое значение, большее вашего значения хи-квадрат. Посмотрите на соответствующее p-значение вверху вашего столбца. Ваше p-значение находится между этим числом и следующим за ним (тем, которое находится левее вашего).

Таблицы с распределением хи-квадрат можно получить из множества источников (вот по этой ссылке можно найти одну из них).

Пример: Наше значение критерия хи-квадрат было равно 3. Так как мы знаем, что в нашем эксперименте всего 1 степень свободы, выберем самую первую строку. Идем слева направо по данной строке, пока не встретим значение, большее 3, нашего значения критерия хи-квадрат. Первое, которое мы находим это 3.84. Смотрим вверх нашего столбца, и видим, что соответствующее p-значение равно 0.05. Это означает, что наше p-значение между 0.05 и 0.1 (следующее p-значение в таблице по возрастанию).

7. Решите, отклонить или оставить вашу нулевую гипотезу

Так как вы определили приблизительное p-значение для вашего эксперимента, вам необходимо решить, отклонять ли нулевую гипотезу вашего эксперимента или нет (напоминаем, это гипотеза о том, что экспериментальные переменные, которыми вы манипулировали не повлияли на наблюдаемые вами результаты). Если ваше p-значение меньше, чем ваш уровень значимости – поздравляем, вы доказали, что очень вероятна связь между переменными, которыми вы манипулировали и результатами, которые вы наблюдали. Если ваше p-значение выше, чем ваш уровень значимости, вы не можете с уверенностью сказать, были ли наблюдаемые вами результаты результатом чистой случайности или манипуляцией вашими переменными.

Пример: Наше p-значение находится между 0,05 и 0,1. Это явно не меньше, чем 0,05, поэтому, к сожалению, мы не можем отклонить нашу нулевую гипотезу. Это означает, что мы не достигли минимум 95% вероятности того, чтобы сказать, что полиция в нашем городе выдает штрафы красным и синим автомобилям с такой вероятностью, которая достаточно сильно отличается от средней по стране.

Другими словами, существует 5-10% шанс, что наблюдаемые нами результаты – это не последствия смены места (анализа города, а не всей страны), а просто случайность. Так как мы потребовали точности меньше чем 5%, мы не можем сказать что мы уверены в том, что полиция нашего города менее предвзято относится к красным автомобилям – существует небольшая (но статистически значимая) вероятность, что это не так.

Источник

Глава 8. Достоверность различий показателей

Одним из самых распространенных классов задач в здравоохранении является оценка различий между показателями. И в повседневной работе, при оперативном управлении объектами здравоохранения, и при проведении специальных исследований, при анализе какой-то специфической информации часто приходиться сравнивать величины показателей между собой. В одних случаях разница между сравниваемыми числами бросается в глаза и, что называется, очевидна, в других – нет. Но все это – субъективные ощущения: очевидное для одного человека может не быть таковым для другого. Поэтому следует взять за правило: никогда не полагаться только на свои субъективные чувства и интуицию, а всегда, даже в самых очевидных случаях, опираться на объективные способы оценки.

Среди широко распространенных в здравоохранении и относительно простых способов оценки достоверности различий показателей первое место по праву принадлежит использованию коэффициента достоверности Стьюдента – t.

В данной главе будут рассмотрены варианты применения коэффициента Стьюдента для сравнения различных видов показателей.

8.1. Сравнение средних арифметических.

Чтобы определить, существенны ли различия между двумя средними, необходимо вычислить их средние ошибки (см. тему 7.3.) и провести расчеты по формуле:

— сравниваемые средние,

в абсолютном выражении;

— соответствующие ошибки

сравниваемых средних величин

Если получена величина t > 2, различия между средними следует признать существенными (достоверными) с вероятностью ошибочности этого заявления менее 5% (р 2,5 различия признаются существенными с вероятностью ошибочности этого заявления менее 2% (р 3,3 различия еще более существенны (р 0,05).

Не следует путать существенность, достоверность различий с силой связи между признаками, что иногда встречается при отсутствии достаточного опыта в проведении анализа.

В качестве примера рассмотрим следующие данные.

В больнице в 1998 году средний срок пребывания на койке составил 19+1,0 дня. С целью сокращения сроков пребывания на койке были внедрены специально разработанные мероприятия, и в 1999 году этот показатель составил 17+1,0 дня. Вопрос: достоверны ли различия в средних сроках пребывания на койке в 1998 г. и в 1999 г., другими словами – можно ли считать сокращение показателя на 2 дня закономерным и воспринимать как следствие внедренных мероприятий?

1,4 0,05) и находятся в пределах случайных колебаний этих показателей в данных условиях.

Следует подчеркнуть, что на основании полученных результатов говорить о недейственности мероприятий нельзя: различия не выявлены, разница в 2 дня находится в пределах случайных колебаний, но этот может обусловливаться недостаточностью числа наблюдений.

Видоизменим данные: 19 дней – средний срок пребывания, рассчитанный по данным всех однотипных больниц области, а не по одному стационару. В таком случае многократно вырастет число наблюдений, что значительно уменьшит ошибку показателя. Предположим он стал равен m = +0,4, а в 1999 г. 15 +0,6.

Вывод: различия существенны, достоверны (p

Пример. В 1999 году проведено 350 операций определенного вида; осложнения наблюдались у 52 прооперированных. В 2000 году – 500 таких же операций; осложнения – у 125 человек.

Необходимо сопоставить показатели доли послеоперационных осложнений.

52 х 100 125 х 100

m1 = = +1,91; m2 = = +1,94;

Вывод: различия в показателях доли послеоперационных осложнений достоверны (р 2,0

Вывод: различия в уровнях заболеваемости в цехах № 1 (168 случаев на 100 раб.) и № 2 (130 случаев на 100 раб.) достоверны (р 2,5

Вывод: различия уровней заболеваемости в цехе № 1 (1100 дней на 100 раб.) и № 2 (1200 дней на 100 раб.) достоверны (р 0,05).

Доля длительно и часто болеющих (ДЧБ) на предприятии Н составила 16,5 ± 0,8 %. В среднем по всем предприятиям города этот показатель равен 14,8 %. Есть ли различия между показателями?

Источник

Оценка достоверности отличий по t-критерию Стьюдента

Критерий называется «несвязанным», потому что сравниваемые группы составлены из разных людей. Связанный t-критерий (который иногда называют парным t-критерием) предназначен для сравнения показателей двух групп, между членами которых существует специфическая связь. Это означает, что каждому члену первой группы соответствует какой-либо член второй группы, который похож на него по какому-то параметру, интересующему исследователя. Чаще всего сравниваются параметры одних и тех же людей до и после определенного события или воздействия (например, в процессе проведения лонгитюдного исследования или формирующего эксперимента). Поэтому данный критерий используется для сравнения показателей одних и тех же людей до и после обследования, эксперимента или прошествии некоторого времени.

В случаях, когда данные не подчиняются нормальному закону распределения, используются непараметрические критерии, эквивалентные t-критериям. Это критерий Манна-Уитни, который эквивалентен непарному t— критерию, и двухвыборочный критерий Вилкоксона, эквивалентный парному t-критерию.

С помощью t-критериев и их непараметрических эквивалентов можно лишь сравнивать результаты двух групп, полученные с использованием одного и того же теста. Однако в некоторых случаях возникает необходимость сравнения нескольких групп или оценок нескольких видов. Это можно сделать поэтапно, разбив задачу на несколько пар сравнений (например, если надо сравнить группы А, Б и В по результатам тестов Х и У, то можно с помощью t-критерия сначала сравнить группы А и Б по результатам теста X, потом А и Б по результатам теста У, А и В по результатам теста Х и так далее). Однако это очень трудоемкий метод; кроме того, по некоторым причинам, в объяснение которых мы не будем здесь углубляться, при его использовании резко возрастает вероятность совершения ошибки первого рода. Поэтому необходим более сложный метод, метод дисперсионного анализа, который требует использования прикладных программ и силу определенной сложности нами не рассматривается

Данная оценка часто необходима при сравнительном анализе полярных групп. Эти группы можно выделить, учитывая различную выраженность определенного целевого признака (характеристики) изучаемого явления. Какими критериями при этом руководствоваться мы указывали выше. Обычно анализ начинают с подсчета первичных статистик выделенных групп, затем оценивают достоверность отличий. Он вычисляется по формуле:

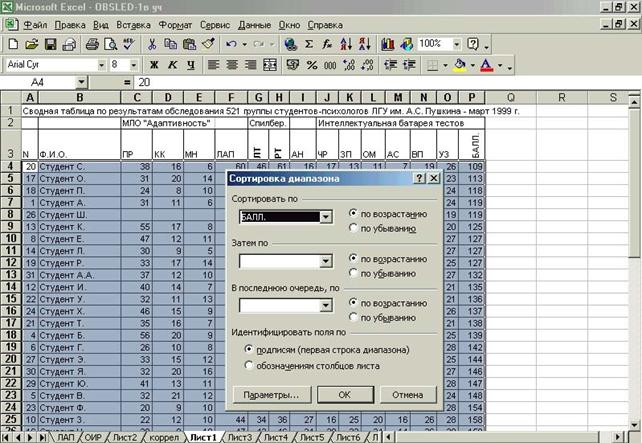
Рисунок 7.17 – Сортировка по шкале «Балл» (Р)

Данные отсортированы по возрастанию, начиная от меньшего показателя признака к большему. Затем начинается творческая работа исследователя. Поскольку выборка одна и подчиняется закону нормального распределения признака, то следует в ней определить крайние границы «успешных» и «не успешных» по интеллекту. В целом, можно придерживаться правила, что 50% признаков от средней арифметической составляют популяционную норму, а следовательно, из расчетов должны быть исключены. Однако, в практике эти границы можно варьировать, но в разумных пределах, при определении подвыборок в основной выборке.

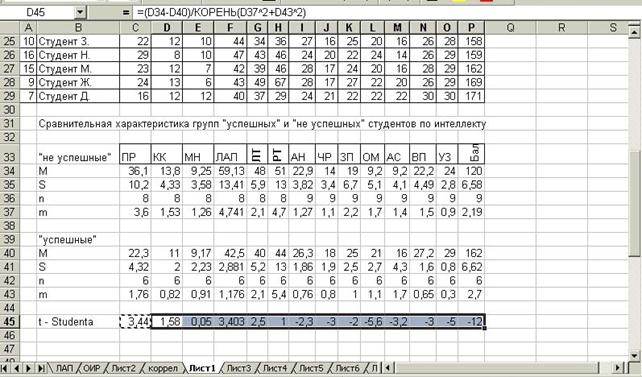
Рисунок 7.18 – вычисление первичных статистик по подвыборкам

Алгоритм вычисления t-критерия Стьюдента:

Курсор помещаем в ячейку С 45 (см. Рисунок 7.18) и на клавиатуре небираем формулу вычисления t-критерия. Напоминаем как она выглядит и ее вид при введении через клавиатуру в программе Excel.

t St =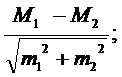

= (С 34 – С 40)/корень(C 37^2 + C 43^2)

Обращаем внимание, формула набирается только в английском шрифте, за исключение слова «корень», после чего не забудьте вновь переключиться на английский. Будьте внимательны в соблюденнии знаков и их порядка.

С 34 –координаты М₁ – «не успешных».

С 40 –координаты М₂ – «успешных».

Набирается следующим образом: нажимаем одновременно две клавиши

«Shift + 6» и появляется значок ^ показателя степени. Затем, набираем

квадрат числа – 2.

C 37 –координаты m₁ – «не успешных».

C 43 –координаты m₁ – «не успешных».

Далее > ОК, появляется вычисленное значение t-критерия для значений признака данного столбца – 3,44. Копируем эту ячейку. Выделяем область втавки по другими сталбцами признаков – «Вставить» > появляются вычисленные значения для других столбцов признаков.

Затем обращаемся к таблице «Квантили t-распределения Стьюдента для доверительной вероятности (1-а = 0,95; 0,99; 0,999)» (см. Приложение 4). Вычисляем число степеней свободы по формуле v = d = n₁ + n₂ – 2,для нашего примера v =6 + 9 – 2 = 13. Выписывем критические значения для p

Дата добавления: 2018-06-01 ; просмотров: 28241 ; Мы поможем в написании вашей работы!

Источник