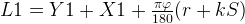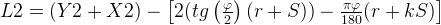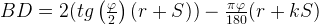Как посчитать длину развертки прутка

Расчет длины развертки

Как я и обещал в комментариях к статье «Расчет усилия листогиба», сегодня поговорим о расчете длины развертки детали, согнутой из листового металла. Конечно, процессу гибки подвергают не только детали из листов. Гнут детали круглого и.

. квадратного сечений, гнут и все прокатные профили – уголки, швеллеры, двутавры, трубы. Однако холодная гибка деталей из листового металлопроката, безусловно, является наиболее распространенной.

Для обеспечения минимальных радиусов, детали перед гибкой иногда нагревают. При этом повышается пластичность материала. Используя гибку с калибрующим ударом, добиваются того, что внутренний радиус детали становится абсолютно равным радиусу пуансона. При свободной V-образной гибке на листогибе внутренний радиус получается на практике больше радиуса пуансона. Чем более у материала детали ярко выражены пружинные свойства, тем более отличаются друг от друга внутренний радиус детали и радиус пуансона.

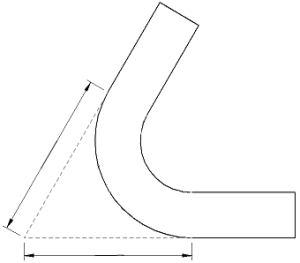
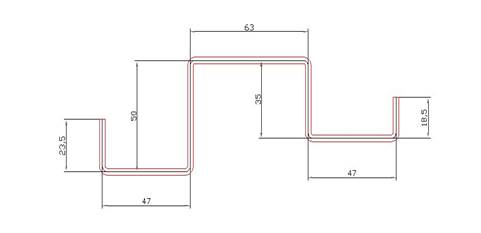
На рисунке, представленном ниже, изображен согнутый из листа толщиной s и шириной b уголок. Необходимо найти длину развертки.

Расчет развертки выполним в программе MS Excel.

Но вся проблема в том, что нейтральный слой располагается не в середине сечения металла! Для справки: нейтральный слой – поверхность расположения условных волокон металла, не растягивающихся и не сжимающихся при изгибе. Более того – эта поверхность (вроде как) не является поверхностью кругового цилиндра. Некоторые источники предполагают, что это параболический цилиндр…

На базе этой формулы и создана программа расчета развертки листовых деталей из сталей марок Ст3 и 10…20 в Excel.

В ячейках со светло-зеленой и бирюзовой заливкой пишем исходные данные. В ячейке со светло-желтой заливкой считываем результат расчета.

1. Записываем толщину листовой заготовки s в миллиметрах

в ячейку D 3 : 5,0

2. Длину первого прямого участка L1 в миллиметрах вводим

в ячейку D 4 : 40,0

3. Внутренний радиус сгиба первого участка R1 в миллиметрах записываем

в ячейку D 5 : 5,0

4. Угол сгиба первого участка a1 в градусах пишем

в ячейку D 6 : 90,0

5. Длину второго прямого участка детали L2 в миллиметрах вводим

в ячейку D 7 : 40,0

6. Все, результат расчета — длина развертки детали L в миллиметрах

в ячейке D 17 : =D4+ЕСЛИ(D5=0;0;ПИ()/180*D6*D3/LN ((D5+D3)/D5))+ +D7+ЕСЛИ(D8=0;0;ПИ()/180*D9*D3/LN ((D8+D3)/D8))+D10+ +ЕСЛИ(D11=0;0;ПИ()/180*D12*D3/LN ((D11+D3)/D11))+D13+ +ЕСЛИ(D14=0;0;ПИ()/180*D15*D3/LN ((D14+D3)/D14))+D16 =91.33

Используя предложенную программу, можно рассчитать длину развертки для деталей с одним сгибом – уголков, с двумя сгибами – швеллеров и Z-профилей, с тремя и четырьмя сгибами. Если необходимо выполнить расчет развертки детали с большим числом сгибов, то программу очень легко доработать, расширив возможности.

Важным преимуществом предложенной программы (в отличие от многих аналогичных) является возможность задания на каждом шаге различных углов и радиусов гибки.

А «правильные» ли результаты выдает программа? Давайте, сравним полученный результат с результатами расчетов по методике изложенной в «Справочнике конструктора-машиностроителя» В.И. Анурьева и в «Справочнике конструктора штампов» Л.И. Рудмана. Причем в расчет возьмем только криволинейный участок, так как прямолинейные участки все, надеюсь, считают одинаково.

Проверим рассмотренный выше пример.

«По программе» : 11,33 мм – 100,0%

«По Анурьеву» : 10,60 мм – 93,6%

«По Рудману» : 11,20 мм – 98,9%

Увеличим в нашем примере радиус гибки R1 в два раза — до 10 мм. Еще раз произведем расчет по трем методикам.

«По программе» : 19,37 мм – 100,0%

«По Анурьеву» : 18,65 мм – 96,3%

«По Рудману» : 19,30 мм – 99,6%

Таким образом, предложенная методика расчетов выдает результаты на 0,4%…1,1% больше, чем «по Рудману» и на 6.4%…3,7% больше, чем «по Анурьеву». Понятно, что погрешность существенно уменьшится, когда мы добавим прямолинейные участки.

«По программе» : 99,37 мм – 100,0%

«По Анурьеву» : 98,65 мм – 99,3%

«По Рудману» : 99,30 мм – 99,9%

Возможно Рудман составлял свои таблицы по этой же формуле, которую использую я, но с погрешностью логарифмической линейки… Конечно, сегодня «на дворе» двадцать первый век, и рыскать по таблицам как-то не с руки!

В заключение добавлю «ложку дегтя». Длина развертки — это очень важный и «тонкий» момент! Если конструктор гнутой детали (особенно высокоточной (0,1 мм)) надеется расчетом точно и с первого раза определить ее, то он зря надеется. На практике в процесс гибки вмешается масса факторов – направление проката, допуск на толщину металла, утонение сечения в месте изгиба, «трапециевидность сечения», температура материала и оснастки, наличие или отсутствие смазки в зоне гибки, настроение гибщика… Короче, если партия деталей большая и дорого стоит – уточните практическими опытами длину развертки на нескольких образцах. И только после получения годной детали рубите заготовки на всю партию. А для изготовления заготовок для этих образцов, точности, которую обеспечивает программа расчета развертки, хватит с лихвой!

Программы расчета «по Анурьеву» и «по Рудману» в Excel можете найти в Сети.

Жду ваших комментариев, коллеги.

Для УВАЖАЮЩИХ труд автора — скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписная форма — чуть ниже и наверху страницы).

Для ОСТАЛЬНЫХ — можно скачать просто так.

Ссылка на скачивание файла: raschet-dliny-razvertki (xls 36,5KB).

Продолжение темы — в статье о К-факторе.

О расчете развертки при гибке труб и прутков читайте здесь.

Источник

Определение длины развертки при гибке

Элементы заготовки, расположенные в деформируемой зоне и прилегающие к внутренней поверхности изгибаемой детали (со стороны пуансона), подвергаются сжатию, а прилегающие к внешней поверхности (со стороны матрицы)—растяжению. Между растянутыми и сжатыми волокнами находится нейтральная линия длина которой не изменяется (Черт. 106).

Черт. 106

Радиус нейтральной линии R в мм (черт. 106) определяется по формуле

где r — радиус гибки, мм;

s— толщина материала мм;

x — коэффициент, величина которого зависит от отношения r/s (табл. 48).

Таблица 48

При завивке шарниров (петель) вследствие наличия внешних сил трения, препятствую­щих деформированию, коэффициент х определяется по табл. 48а.

Таблица 48а

Длина развертки изгибаемой детали L_р в мм (черт. 107) определяется по фор­муле

R₁; R₂; R₃ — радиусы нейтральной линии, определяемые по формуле (46).

Черт. 107

При гибке материалов толщиной свыше 3 мм под углом 90° с радиусом гибки r≤s радиус нейтральной линии R, рассчитанный по формуле (46), должен быть скорректи­рован до величины R₁ (черт. 108), исходя из условия целостности материала и сопряжения в точках а и а₁ криволинейного участка радиусом R₁ с прямыми а—а и а₁—а₁, преходящими через середину толщины s. На участке С—С₁ пунктиром показан внешний контур при расчете без учета утонения материала. В связи с утонением при гибке толщина s₁ на этом участке меньше исходной s.

Черт. 108

Значения R₁ радиуса скорректированной нейтральной линии и длину дуги abа₁, следует подсчитать по формулам

R — определяется по формуле (46); r — радиус гибки, мм; остальные обозначения показаны на черт. 108.

Элементы для определения размеров разверток часто применяемых гнутых деталей приведены в табл. 49.

Таблица 49

Источник

Гибка трубы. Длина развертки в Excel!

При проектировании и изготовлении гнутых деталей из труб и прутков всегда возникает задача определения длины развертки – длины прямолинейной заготовки до начала технологического процесса гибки.

. расчета длины разверток деталей, согнутых из листового металла прямоугольного сечения, представляю расчет в Excel длины развертки деталей из прутков и труб круглого сечения.

Программа расчета написана по формуле классического сопромата! Практические результаты будут немного отличаться от рассчитанных значений из-за целого ряда факторов, о которых уже упоминалось в статье о гибке листовых заготовок (ссылка на эту статью в предыдущем абзаце). Однако точность при гибке трубы для изготовления опытного образца представленная ниже программа обеспечит.

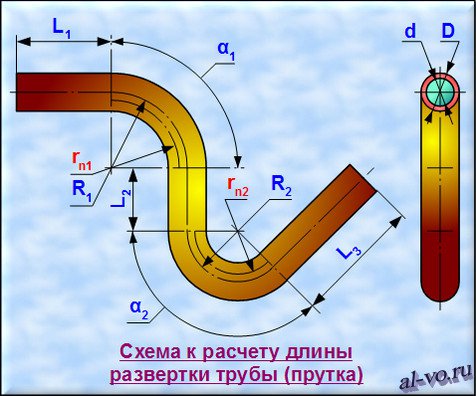
Ниже этого текста на рисунке представлена расчетная схема.

Радиусы нейтральных слоев каждого из изогнутых участков рассчитываются по формуле:

r_ni =((4* R_i 2 — D 2 ) 0,5 +(4* R_i 2 — d 2 ) 0,5 )/4

Нейтральный слой – это поверхность, ближе которой к центру радиуса изгиба материал трубы при гибке сжимается, а дальше которой от центра радиуса изгиба – растягивается.

Длина кривых участков при гибке трубы определяется по формуле:

Здесь угол α_i должен быть в градусах.

Общая длина развертки вычисляется суммированием длин прямых и изогнутых участков:

L = ∑( L_i + l_i )

Программа расчета в Excel длины развертки при гибке труб.

Для выполнения расчетов используем программу MS Excel. Можно воспользоваться табличным процессором Calc из свободно распространяемых пакетов Apache OpenOffice или LibreOffice.

Исходные данные:

Положим, что в рассматриваемом примере деталь состоит из трех прямых и двух изогнутых участков (как на схеме вверху).

1. Записываем наружный диаметр трубы D в миллиметрах

в ячейку D4: 57,0

2. Значение внутреннего диаметра трубы d в миллиметрах заносим

в ячейку D5: 50,0

Внимание. Если рассчитывается длина развертки прутка сплошного круглого сечения, то d =0!

3. Длину первого прямого участка L₁ в миллиметрах вводим

в ячейку D6: 200,0

4. Осевой радиус сгиба первого кривого участка R₁ в миллиметрах записываем

в ячейку D7: 300,0

5. Угол сгиба первого кривого участка α₁ в градусах пишем

в ячейку D8: 90,0

6. Длину второго прямого участка детали L₂ в миллиметрах вводим

в ячейку D9: 100,0

7. Осевой радиус сгиба второго изогнутого участка R₂ в миллиметрах записываем

в ячейку D10: 200,0

8. Угол сгиба второго изогнутого участка α₂ в градусах пишем

в ячейку D11: 135,0

9. Длину третьего прямого участка детали L₃ в миллиметрах вводим

в ячейку D12: 300,0

10-15. Ввод исходных данных в Excel для нашего примера завершен. Ячейки D13…D18 оставляем пустыми.

Программа позволяет рассчитывать развертки деталей, содержащих до пяти прямых участков и до четырех изогнутых. Гибка трубы с большим количеством участков требует для расчета развертки незначительной модернизации программы.

Результаты расчетов:

16. Длину первого изогнутого участка L₁ в миллиметрах вычисляем

в ячейке D20: =ЕСЛИ(D7=0;0;ПИ()*D8/180*((4*D7^2-$D$4^2)^0,5+(4*D7^2-$D$5^2)^0,5)/4) =469,4

17. Длину второго изогнутого участка L₂ в миллиметрах вычисляем

в ячейке D21: =ЕСЛИ(D10=0;0;ПИ()*D11/180*((4*D10^2-$D$4^2)^0,5+(4*D10^2-$D$5^2)^0,5)/4) =467,0

18-19. Так как в рассматриваемом примере нет третьего и четвертого кривых участков, то

в ячейке D22: =ЕСЛИ(D13=0;0;ПИ()*D14/180*((4*D13^2-$D$4^2)^0,5+(4*D13^2-$D$5^2)^0,5)/4) =0,0

в ячейке D23: =ЕСЛИ(D16=0;0;ПИ()*D17/180*((4*D16^2-$D$4^2)^0,5+(4*D16^2-$D$5^2)^0,5)/4) =0,0

20. Общая длина развертки детали L в миллиметрах суммируется

в ячейке D24: =D6+D9+D12+D15+D18+D20+D21+D22+D23 =1536,3

Длина развертки изогнутой трубы рассчитана с помощью программы MS Excel.

Заключение.

Гибка трубы и/или прутка – не простая технологическая задача, таящая целый ряд «подводных камней». Надеюсь, предложенный расчет в Excel упростит вам, уважаемые читатели, ее решение. Возможность задания на каждом шаге различных длин прямых участков, углов и радиусов гибки, несомненно, расширит область применения представленной программы.

Уважаемые читатели! Вопросы, отзывы, и замечания оставляйте, пожалуйста, в комментариях внизу страницы.

УВАЖАЮЩИМ труд автора скачать файл можно ПОСЛЕ ПОДПИСКИ НА АНОНСЫ СТАТЕЙ (подписные формы — чуть ниже и наверху страницы).

ОСТАЛЬНЫМ — можно скачать просто так.

Ссылка на скачивание файла: raschet-dliny-razvertki-truby (xls 103KB).

Статьи с близкой тематикой

Отзывы

30 комментариев на «Гибка трубы. Длина развертки в Excel!»

Как хорошо, что такие люди как Вы есть. Спасибо за Ваше неравнодушие.

Александр спасибо вам огромное, что подробно расказываете и выкладываете расчет. Гибка труб — действительно нужное знание для инженеров и конструкторов. Пригодится даже в дом. хозяйстве. Успехов.

Большое спасибо за ценный материал.

А можно ли применить этот подход, если пруток — квадратного сечения? Например пересчитать площадь сечения в эквивалентный диаметр?

Александр, конечно, можно. Вы только что читали статью «Расчет длины развертки», где приведена формула для прямоугольного сечения. Квадрат — это тоже прямоугольник!

Доброе время суток. А как насчет материала 316 (нерж).

Так как формула расчета взята из классического сопромата, то применима для любых материалов, обладающих упругостью и пластичностью.

Перечитайте третий абзац статьи.

Большое Вам спасибо за безвозмездную помощь.

Гнем трубу буквой П. Исходные данные:

Внешний диаметр — 45мм

Внутренний диаметр — 42,6мм (стенка трубы 1,2мм)

Длина первого прямого участка — 375,5мм

Осевой радиус — 70мм

Длина второго прямого участка — 175мм

Осевой радиус — 70мм

Длина третьего прямого участка — 375,5мм

По Вашим расчетам получаем длину разверки — 1203,3мм

Если считать развертку по длине осевой линии: 375,5мм х 2шт + 175мм + 109,95 (длина дуги=пирн/180) х 2шт = 1145,9мм

1203,3-1145,9 = 57,4мм — расхождение

По моим расчетам получаем длину развертки — 1134,9мм!

Не знаю откуда Вы взяли 1203,3?

Если считать по осевой линии — 1145,9.

Заготовку следует взять на 11,0 мм короче, чем получается по осевой линии.

Добрый день! Как рассчитать длину трубы, имея уже согнутую заготовку. Исходные данные:

Диаметр трубы — 32мм, толщина стенки 1,2мм, согнута в одной плоскости буквой П. Если рулеткой измерять периметр по наруже, получаем 1147мм(сумма трех сторон с радиусами).

Добрый день! Владимир, вспомните геометрию.

Не зная радиусов и линейных размеров ответить на Ваш вопрос нельзя.

В формуле используются какие либо коэффициенты привязаные к материалу? Нужно рассчитать длину медной трубы.

Если Вы внимательно посмотрите на входящие в формулу параметры, то увидите, что они все чисто геометрические. Нет и намека на характеристики материала.

Дело в том, что классический сопромат рассматривает (в основном) материалы, обладающие при растяжении зоной упругой деформации, площадкой текучести, участком пластической деформации приводящим к точке разрушения. Так вот схожими по виду (не по величинам нагрузок и деформаций) диаграммами растяжения обладают все, так называемые, пластичные материалы. К ним относятся многие металлы, а вот закаленные стали, стекло, бетон — нет. Так их никто и не гнет!

Эта формула — теоретически выведенная для материалов с идеальной площадкой текучести. Но как и идеального газа (помните физику?), так и идеального металла в природе нет. Но с очень близкими диаграммами растяжения — полно.

Если точность в 3. 5% Вас не устраивает, то можно найти массу таблиц разных исследователей, которые определяют длину разверток для различных материалов опытным путем.

Резюме: эта формула для всех пластичных металлов. Её можно найти во многих учебниках по сопромату.

На практике многие вообще считают развертки труб по средней линии. Полученные погрешности «съедаются» низкой точностью оборудования и еще десятком факторов.

Спасибо Вам! За изложенный материал, где все так доходчиво расписано.

Расчет точен только при сгибе на 90 градусов. Если угол выше 90, длина кривого участка в 1,5-2 больше реальной длины.

Андрей, приведите свой пример.

В примере, приведенном в статье, 2-ой кривой участок с углом 135 градусов считается верно!

Может подскажите какие формулы использовать для расчета длинны развертки не круглой, а квадратной или прямоугольной трубы.

Если нужны формулы для очень точного расчета с учетом смещения нейтрального слоя относительно центра тяжести сечения, то — не подскажу.

Если радиусы изгиба в

5 и более раз больше размера сечения и не требуется точность «до миллиметра», то — считайте по осевой линии (линии центров тяжести сечений).

Спасибо, вы мне помогли сохранить время!))

Александр, добрый день.

Спасибо огромное за ваши труды!

А не подскажите в каком учебнике можно посмотреть вывод формулы для расчёта радиусов нейтральных слоёв у труб?

Заранее спасибо за ответ!

В каком-то из учебников по сопромату. По-быстрому вспомнить и найти в каком именно — не получилось.

Добрый день, мне необходимо согнуть круглую трубу (диаметр 25, стенка 1мм) в форму прямоугольника 50*40 см. Как произвести расчет?

Как посчитать? Так, как написано выше в статье.

Только для такой тонкостенной трубы необходимо задать достаточно большой радиус изгиба, иначе сечение при изгибе деформируется. В итоге такой небольшой прямоугольник Вам получить будет трудно. В углах будут слишком большие радиусы.

Решения — горячая штамповка, гибка с дорном, гибка с набивкой сечения песком, вварка в углы горячештампованных крутых отводов.

Последний вариант — самый простой и дешевый.

(Минимальные радиусы холодной гибки труб из различных металлов смотрите в справочниках.)

Задайте угрл 359 градусов, должно получить длина первого участка приблизительно в 2 раза больше радиуса, но не как в 5 раз больше радиуса

Смеющийся Архимед по ночам не снится? 🙂

Чисто практические решения повседневных (спонтанно появляющихся) задач. Но — проработанные, и не на глазок.

Вопрос смежный с темой этой странички: Расчёт роликов для гибки трубы с учётом свойств материала и диапазонов деформации (На грани смятия маленькие) (большие, практически без остаточной упругой деформации).

Материалы: от мельхиора и меди, до нержавейки и жаропрочной стали.

На данный момент подгонка осуществляется корректирующим точением заведомо большего огибаемого ролика (долго зачастую).

Борис, спасибо за высокую оценку материалов сайта.

Но в чем вопрос? Не очень понятно без схемы.

Собственно схема не нужна.

Диаметр обкатываемого ролика отличается от искомого на величину упругой деформации (чаще речь идёт о гибке на 180 градусов). Причём просто подгонка межосевого расстояния не всегда возможна, поскольку гнутые элементы «вложены» друг в друга и зазор между трубами лимитирован по всей длине, в том числе и в радиусной части.

Приходится ловить радиус гибки с точностью до десяток.

Применение «в лоб» коэффициента упругости из свойств материала не помогает. И коэффициент соотношения радиуса гибки к радиусу ролика плавает в зависимости от крутизны гиба.

Собственно пока писал — осознал, что вывести зависимость поможет только собственная статистика.

Но — вдруг! Может толкнёте к чему?

Большое СПАСИБО за программу расчетов длины развертки. Пользоваться ей очень легко, очень круто и мне хватало 5 прямых участков, но когда мне нужно стало иметь в программе 8 и больше прямых участков. я быстренько и простенько продолжил Ваши формулы и все готово! Большущее СПАСИБО ВАМ ЗА ВАШ ТРУД. ЖЕЛАЮ ЗДОРОВЬЯ, СЧАСТЬЯ, ВСЕХ БЛАГ. С НАСТУПАЮЩИМ НОВЫМ 2022 ГОДОМ ВАС.

Источник

Расчет длины развертки детали

Расчет размеров заготовки при гибке

14.05.2015 Опубликовал Mehanolog 1

Рассмотрим ситуацию, которая нередко возникает на гибочном производстве. Особенно это касается небольших цехов, которые обходятся средствами малой и средней механизации. Под малой и средней механизацией я подразумеваю использование ручных или полуавтоматических листогибов. Оператор суммирует длину полок, получает общую длину заготовки для требуемого изделия, отмеряет нужную длину, отрезает и.. после гибки получает неточное изделие. Погрешности размеров конечного изделия могут быть весьма значительными (зависит от сложности изделия, количества гибов и т.д.). Все потому, что при расчетах длины заготовки нужно учитывать толщину металла, радиус гибки, коэффициент положения нейтральной линии (К-фактор). Именно этому и будет посвящена данная статья.

Честно говоря, произвести расчет размеров заготовки несложно. Нужно только понять, что нужно брать в расчет не только длины полок (прямых участков), но и длины криволинейных участков, получившихся ввиду пластических деформаций материала при гибке.

Притом, все формулы уже давно выведены «умными людьми», книги и ресурсы которых я постоянно указываю в конце статей (оттуда вы, при желании, можете получить дополнительные сведения).

Таким образом, для расчета правильной длины заготовки (развертки детали), обеспечивающей после гибки получение заданных размеров, необходимо, прежде всего, понять, по какому варианту мы будем производить расчет.

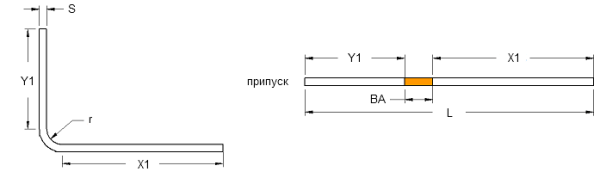
Вариант 1	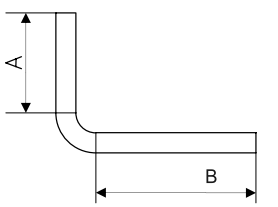Вариант 2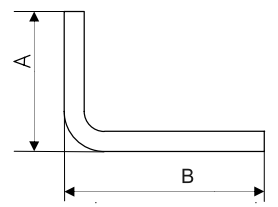
Lt = A + B + BA	Lt = A + B – BD
Lt – общая длина плоской заготовки; А и В – см. рисунок; ВА– припуск	Lt – общая длина плоской заготовки; А и В – см. рисунок; BD – вычет

Таким образом, если вам нужна поверхность полки А без деформаций (например для расположения отверстий), то вы ведете расчет по варианту 1. Если же вам важна общая высота полки А, тогда, без сомнения, вариант 2 более подходящий.

Вариант 1 (с припуском)

а) Определить К-фактор (см Справочную);

б) Разбить контур изгибаемой детали на элементы, представляющие собой отрезки прямой и части окружностей;

в) Суммировать длины этих отрезков. При этом, длины прямых участков суммируются без изменения, а длины криволинейных участков – с учетом деформации материала и соответственного смещения нейтрального слоя.

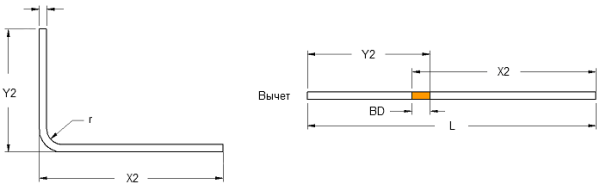
Так, например, для заготовки с одним гибом, формула будет выглядеть следующим образом:

Где X1 – длина первого прямого участка, Y1– длина второго прямого участка, φ – внешний угол, r – внутренний радиус гибки, k – коэффициент положения нейтральной линии (К-фактор), S – толщина металла.

Причем, нам придется считать длину каждой полки отдельно, прежде чем задавать точку перемещения заднего упора станка. Надеюсь, это понятно.

Таким образом, ход расчета будет следующим..

Y1 + BA1 + X1 + BA2 +..т.д

Длина формулы зависит от количества переменных.

Вариант 2 (с вычетом)

По моему опыту, это самый распространенный вариант расчетов для гибочных станков с поворотной балкой. Поэтому, давайте рассмотрим этот вариант.

Нам также необходимо:

а) Определить К-фактор (см таблицу).

б) Разбить контур изгибаемой детали на элементы, представляющие собой отрезки прямой и части окружностей;

в) Рассчитать необходимые вычеты. При этом, длины прямых участков суммируются без изменения, а длины вычетов – соответственно, вычитаются.

Здесь необходимо рассмотреть новое понятие – внешняя граница гибки.

Чтобы было легче представить, см рисунок:

Внешняя граница гибки – вот эта воображаемая пунктирная линия.

Так вот, чтобы найти длину вычета, нужно от длины внешней границы отнять длину криволинейного участка.

Таким образом, формула длины заготовки по варианту 2:

Где Y2, X2 – полки, φ – внешний угол, r – внутренний радиус гибки, k – коэффициент положения нейтральной линии (К-фактор), S – толщина металла.

Вычет у нас (BD), как вы понимаете:

Внешняя граница гибки (OS):

И в этом случае также необходимо каждую операцию рассчитывать последовательно. Ведь нам важна точная длина каждой полки.

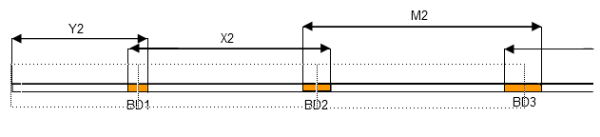
Схема расчета следующая:

(Y2 – BD1 / 2) + (X2 – (BD1 / 2 + BD2 / 2)) + (M2 – (BD2 / 2 + BD3 /2)) +.. и т.д.

Графически это будет выглядеть так:

И еще, размер вычета (BD) при последовательном расчете считать надо правильно. То есть, мы не просто сокращаем двойку. Сначала считаем весь BD, и только после этого получившийся результат делим пополам.

Надеюсь, что этой своей ремаркой я никого не обидел. Просто я знаю, что математика забывается и даже элементарные вычисления могут таить в себе никому не нужные сюрпризы.

На этом все. Всем спасибо за внимание.

При подготовке информации я использовал: 1. Статья «BendWorks. The fine-art of Sheet Metal Bending» Olaf Diegel, Complete Design Services, July 2002; 2. Романовский В.П. «Справочник по холодной штамповке» 1979г; материалы англоязычного ресурса SheetMetal.Me (раздел “Fabrication formulas”, ссылка: http://sheetmetal.me/formulas-and-functions/)

Расчет длины развертки детали

Упрощенно развертка рассчитывается следующим образом:

Допустим, имеется деталь как на рисунке.

Считаем суммарно развертку по СРЕДНЕЙ линии….. примерно так :

Еще необходимо учесть следующее ограничение – минимальное расстояние между гибами или от гиба до края заготовки должно быть не менее 15 мм. Это технологическое ограничение листогиба. Можно и меньше, но это необходимо обсудить. Есть и другие ограничения, но это уже будем решать вместе.

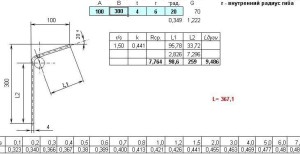
Расчет разверток деталей из листа под углом N°

где каэффициент K определяется по таблице. Он зависит от отношения внутреннего радиуса гибки и толщины материала r/t

Lдуги = pi * G/180 * Rср

Как мы видим r/t (на рисунке r/s) равно1,5.Выбираем из таблицы 1,5 получаем K=0,441

Ну вот получилась прожка.Данный файл xlРасчет разверткиВы можете скачать прямо с сайта.Он сам все расчитает.Нужно только ввести размеры. Если хотите посмотреть как работают формулы,снимите защиту с листа.Пароля нет.

Источник