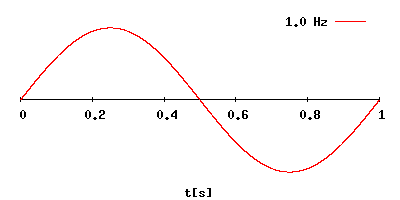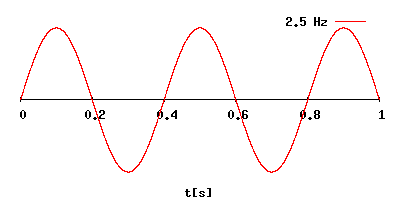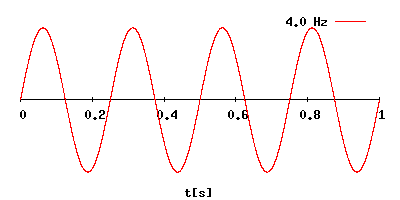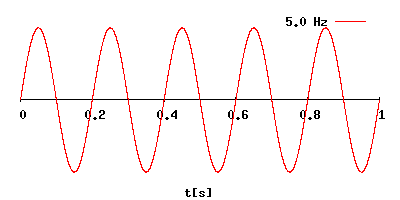
Как посчитать частоту в герцах
Как связаны между собой частота колебаний и период?
Онлайн калькуляторы: перевод частоты колебаний в период и, наоборот –
перевод периода в частоту
Частота (F) в физическом смысле этого слова – это характеристика, равная количеству повторений некого периодического (в нашем случае колебательного) процесса за единицу времени.
Рассчитывается частота, как отношение количества колебаний (повторений) к промежутку времени, за которое они совершены.
Период колебаний (T) – это промежуток времени, за которое совершается 1 полное колебание.
Формула, связывающая эти параметры, крайне проста и в системе СИ выглядит следующим образом:
F(Гц) = 1/T(с) и соответственно: T(с) = 1/F(Гц)
Однако, как показывает практика, не всегда удобно делить единицу на некое число, которое может оказаться довольно громоздким, а параллельно ещё – манипулировать нулями при переводе величин из одних единиц измерений в другие. Поэтому давайте-ка сдобрим пройденный материал парой простых онлайн калькуляторов.
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ПЕРИОДА КОЛЕБАНИЙ ПО ЧАСТОТЕ
А теперь всё то же самое, но наоборот:
ОНЛАЙН КАЛЬКУЛЯТОР РАСЧЁТА ЧАСТОТЫ ПО ПЕРИОДУ КОЛЕБАНИЙ
В некоторых прикладных электротехнических расчётах (для удобства восприятия) используется дополнительная величина – циклическая (круговая, радиальная, угловая) частота, обозначаемая буквой ω. В системе СИ угловая частота выражается в радианах в секунду, а её численное значение равно: ω (рад/с) = 2πF(Гц) .
Формула частоты
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
Единицей измерения частоты в Международной системе единиц (СИ) служат в герцы или обратные секунды:
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами ($<\nu >_1\ и\ <\nu >_2$) равна:
Еще одно величиной характеризующей колебательный процесс является циклическая частота ($<\omega >_0$), связанная с частотой как:
Циклическая частота измеряется в радианах, деленных на секунду:
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
Физический маятник совершает колебания с частотой:
Формулы для вычисления частоты дискретных событий, частота вращения
Единицей измерения частоты дискретных событий является обратная секунда:
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Примеры задач с решением
Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?
Характеристики колебаний
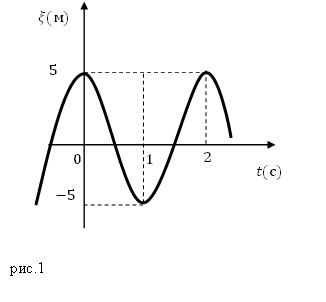
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени \(\large \Delta t\), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина \( \large x \). Тогда символом \( \large x_ <0>\) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
\( \large T \left( c \right) \) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Что такое частота
Обозначают ее с помощью греческой буквы «ню» \( \large \nu \).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
\( \large \nu \left( \frac<1>
Иногда в учебниках встречается такая запись \( \large \displaystyle \nu \left( c^ <-1>\right) \), потому, что по свойствам степени \( \large \displaystyle \frac<1>
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол \(\large 2\pi\) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный \(\large 2\pi\) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
\( \large \displaystyle \omega \left( \frac<\text<рад>>
Примечание: Величину \( \large \omega \) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за \(\large 2\pi\) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный \(\large 2\pi\) секунд?».
Обычная \( \large \nu \) и циклическая \( \large \omega \) частота колебаний связаны формулой:
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину \( \large \omega \), нужно сначала найти период T.
Затем, воспользоваться формулой \( \large \displaystyle \nu = \frac<1>
И только после этого, с помощью формулы \( \large \omega = 2\pi \cdot \nu \) посчитать циклическую \( \large \omega \) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину \( \large \omega \) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный \(\large 2\pi\), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, \(\large \varphi_ <0>\).
\(\large \varphi_ <0>\left(\text <рад>\right) \) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рассмотрим теперь, как величина \(\large \varphi_ <0>\) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы \(\large \varphi_ <0>\) принимаем равной нулю.
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время \(\large \Delta t\), начальный угол \(\large \varphi_ <0>\) будет отличаться от нулевого значения.
Определим угол \(\large \varphi_ <0>\) с помощью графика колебаний.
Обратим внимание (рис. 8) на то, что время, лежащее на горизонтальной оси, измеряется в секундах, а величина \(\large \varphi_ <0>\) — в радианах. Значит, нужно связать формулой кусочек времени \(\large \Delta t\) и соответствующий ему начальный угол \(\large \varphi_ <0>\).
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
\[\large T = 5 – 1 = 4 \left( \text <сек>\right)\]
Из графика следует, что период T = 4 сек.
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
Для этого используем формулу:
\(\large \displaystyle \frac<1> <4>\cdot 2\pi = \frac<\pi > <2>=\varphi_ <0>\)
Значит, интервалу \(\large \Delta t\) соответствует угол \(\large \displaystyle \frac<\pi > <2>\) – это начальная фаза для красной кривой на рисунке.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол \(\large \displaystyle \frac<\pi > <2>\) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая \(\large \varphi_ <0>= 0 \).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину \(\large \varphi_ <0>\) записываем со знаком «-».
Примечания:
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают \(\varphi\).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной \( \varphi_<0>\) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто \( \varphi\) фазой (рис. 10б) – это величина переменная.
Как на графике колебаний отметить фазу
На графике колебаний фаза \(\large \varphi\) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины \(\large \omega\) — циклическая частота и \(\large \varphi_<0>\) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу \(\large \varphi\), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
\( \large \varphi_<01>\) – для первого процесса и,
\( \large \varphi_<02>\) – для второго процесса.
Определим разность фаз между первым и вторым колебательными процессами:
Величина \(\large \Delta \varphi \) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
\( \large T \left( c \right) \) – время одного полного колебания (период колебаний);
\( \large N \left( \text <шт>\right) \) – количество полных колебаний;
\( \large t \left( c \right) \) – общее время для нескольких колебаний;
\(\large \nu \left( \text <Гц>\right) \) – частота колебаний.
\(\large \displaystyle \omega \left( \frac<\text<рад>>
\(\large \varphi_ <0>\left( \text <рад>\right) \) — начальная фаза;
\(\large \varphi \left( \text <рад>\right) \) – фаза (угол) в выбранный момент времени t;
\(\large \Delta t \left( c \right) \) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Частота, период сигнала, изменения напряжения, силы тока. Периодический. Единицы измерения. Герц, Гц, Hz. Hertz. Доли. килогерц, кгц, мегагерц, мгц
Понятие частоты и периода периодического сигнала. Единицы измерения. (10+)
Частота и период сигнала. Понятие. Единицы измерения
Материал является пояснением и дополнением к статье:
Единицы измерения физических величин в радиоэлектронике
Единицы измерения и соотношения физических величин, применяемых в радиотехника.
В природе нередко встречаются периодические процессы. Это означает, что какой-то параметр, характеризующий процесс, изменяется по периодическому закону, то есть верно равенство:
Определение частоты и периода
Понятно, что если верно предыдущее равенство, то верно и такое:
В радиоэлектронике мы исследуем силу тока и напряжение, так что периодическими сигналами будем считать сигналы, для напряжения или силы тока в которых верно соотношение 1.
Вашему вниманию подборка материалов:
Практика проектирования электронных схем Искусство разработки устройств. Элементная база. Типовые схемы. Примеры готовых устройств. Подробные описания. Онлайн расчет. Возможность задать вопрос авторам
Единицы измерения частоты и периода
Частота измеряется, соответственно, в 1 / секунда. Эту единицу измерения еще называют Герц (Hertz) и обозначают Гц (Hz). В зарубежной литературе можно встретить и такое обозначение ‘cycles per second’ (cps).
В природе много видов периодических сигналов. Наиболее распространены синусоидальные, прямоугольные (меандр), треугольные, пилообразные и т. д. Распространены и непериодические сигналы: шум, затухающие колебания, модулированные сигналы.
Частота и период непериодических сигналов
Вообще говоря понятия периода и частоты применимы только к периодическим сигналам. Но в электронике иногда их условно применяют к непериодическим сигналам, например, к затухающим колебаниям, сигналам с амплитудной и широтно-импульсной модуляцией. Это возможно, когда функция зависимости напряжения сигнала от времени может быть представлена, как суперпозиция двух функций, периодической (U2) и непериодической (U1):
Тогда считают, что частота и период итогового сигнала равны частоте и периоду U2.
Например, для затухающих синусоидальных колебаний, амплитуда которых падает обратно-пропорционально времени, формула будет иметь вид:
Единицы измерения, кратные Герцу (Hertz)
Приведем единицы измерения, кратные Герц, чаще всего применяемые в электронике.
| Гигагерц | ГГц | GHz | 1E9 Гц | 1000000000 Гц |
| Мегагерц | МГц | MHz | 1E6 Гц | 1000000 Гц |
| Килогерц | кГц | kHz | 1E3 Гц | 1000 Гц |
К сожалению в статьях периодически встречаются ошибки, они исправляются, статьи дополняются, развиваются, готовятся новые. Подпишитесь, на новости, чтобы быть в курсе.
Если что-то непонятно, обязательно спросите!
Задать вопрос. Обсуждение статьи.
Мобильное управление освещением. Звуковое реле. Включение / выключение.
Звуковое реле и схемы для включения освещения с помощью звонка на мобильный теле.
Частота электрического тока — определение, физический смысл
Переменный ток имеет ряд важных характеристик, влияющих на его физические свойства. Одним из таких параметров является частота переменного тока. Если говорить с точки зрения физики, то частота – это некая величина, обратная периоду колебания тока. Если проще – то это количество полных циклов изменения ЭДС, произошедших за одну секунду.
Известно, что переменный ток заставляет электроны двигаться в проводнике сначала в одну сторону, потом — в обратную. Полный путь «туда-обратно» они совершают за некий промежуток времени, называемый периодом переменного тока. частота же является количеством таких колебаний за 1 секунду.
В республиках бывшего СССР стандартной считается частота тока в 50 Гц.
Это значит, что синусоида тока движется в течение 1 секунды 50 раз в одном направлении, и 50 — в обратном, 100 раз проходя чрез нулевое значение. Получается, что обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.
Для измерения частоты переменного тока применяют приборы, называемые частотомерами. Частотомеры используют несколько основных способов измерения, а именно:
Метод дискретного счета основывается на подсчете импульсов необходимой частоты за конкретный промежуток времени. Его наиболее часто используют цифровые частотомеры, и именно благодаря этому простому методу можно получить довольно точные данные.
Более подробно о частоте переменного тока Вы можете узнать из видео:
Метод перезаряда конденсатора тоже не несет в себе сложных вычислений. В этом случае среднее значение силы тока перезаряда пропорционально соотносится с частотой, и измеряется при помощи магнитоэлектрического амперметра. Шкала прибора, в таком случае, градуируется в Герцах.
Погрешность подобных частотомеров находится в пределах 2%, и поэтому такие измерения вполне пригодны для бытового использования.
Резонансный способ измерения базируется на электрическом резонансе, возникающем в контуре с подстраиваемыми элементами. Частота, которую необходимо измерить, определяется по специальной шкале самого механизма подстройки.
Такой метод дает очень низкую погрешность, однако применяется только для частот больше 50 кГц.
Метод сравнения частот применяется в осциллографах, и основан на смешении эталонной частоты с измеряемой. При этом возникают биения определенной частоты. Когда же частота этих биений достигает нуля, то измеряемая частота становится равной эталонной. Далее, по полученной на экране фигуре с применением формул можно рассчитать искомую частоту электрического тока.
Ещё одно интересное видео о частоте переменного тока: