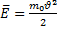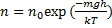газ в поле тяжести
2.1.4. Идеальный газ в поле силы тяжести
Каково поведение идеального газа в поле внешней силы? Для определенности в качестве внешней силы возьмем хорошо известную силу тяжести mg. Под действием внешней силы механическая система частиц приобретает импульс и перемещается как целое поступательно в направлении силы. В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.
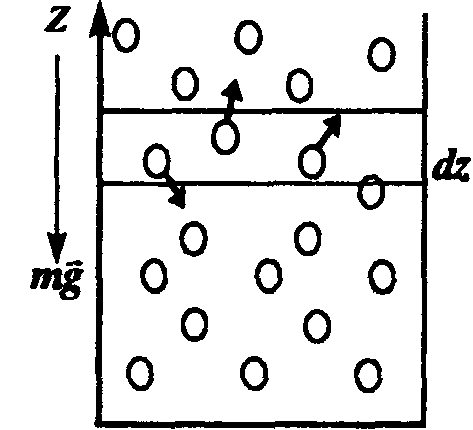
Пусть разность давлений есть dP. Давление газа с ростом высоты уменьшается, поэтомуdP равно весу слоя со знаком минус. Вес газа в объеме слояdV =dz·S равен ρ·g·dV, где ρ — плотность газа,g — ускорение силы тяжести. Таким образом,
По определению 
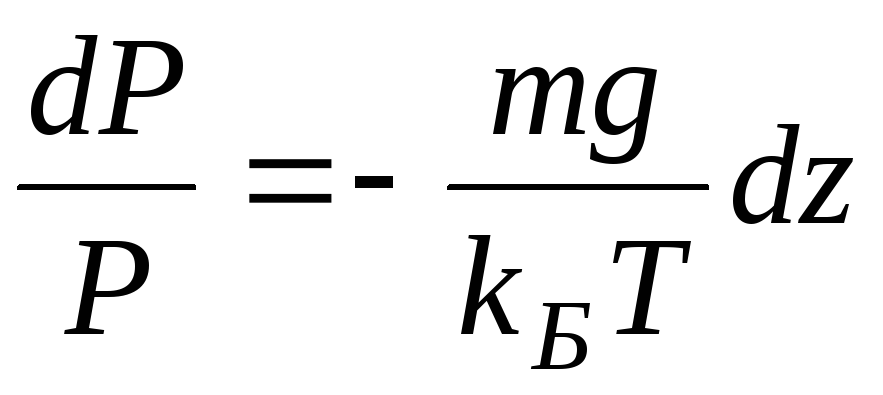
Интегрируя это соотношение, получим 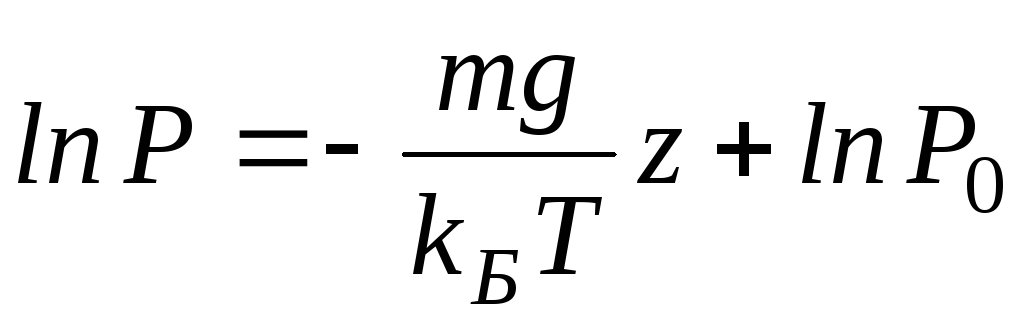
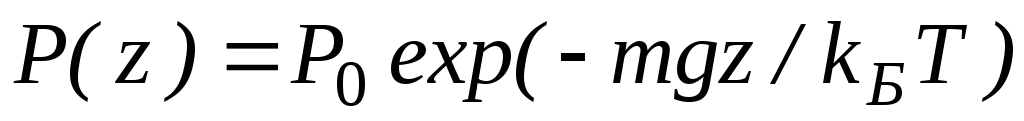
Здесь P0 — давление приz = 0. т. е. у основания столба. Аналогично с высотой изменяется и плотность частиц
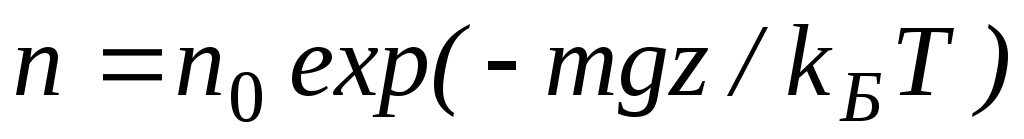
Давление и плотность газа распределены по объему газа неоднородно, они принимают максимальные значения у основания столба и убывают с высотой.
Величина, входящая в показатель экспоненты в формулах (2.9) и (2.10), есть потенциальная энергия частицы в поле тяжести U =mgz-Таким образом, распределение молекул в произвольном потенциальном внешнем поле, в котором частицы обладают потенциальной энергиейU(r), может быть описано формулой:
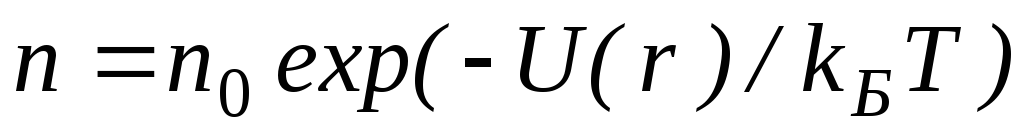
Эта формула называется распределением Больцмана. Здесь n0 — плотность частиц в точках пространства, для которых потенциальная энергия принята равной нулю.
Согласно распределению Больцмана число частиц, обладающих определенными значениями потенциальной энергии определяется отношением величины потенциальной энергии U к тепловой энергии частицыkБT. Чем больше энергия теплового движения, тем более разупорядочена система частиц, значит, тем более однородно распределены частицы в пространстве. В самом деле, еслиkБT >>U,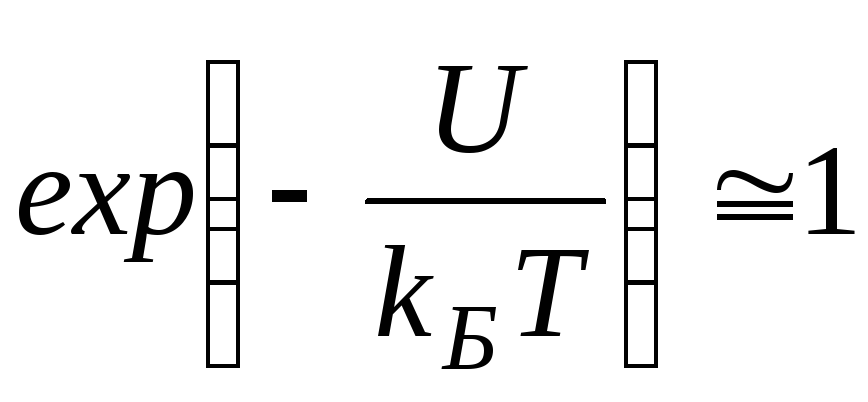
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Идеальный газ в поле силы тяжести. Барометрическая формула.Распределение Больцмана.
Макроскопическая система, макроскопические параметры. Идеальный газ, уравнение состояния идеального газа.
Макроскопические параметры – параметры значения, которых можно определить с помощью приборов, ничего не зная об атомно-молекулярном строении вещества (давление, объем, температура).
Идеальным называют газ, взаимодействием, между молекулами которого можно пренебречь.
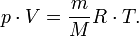
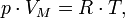
Законы идеальных газов: Бойля-Мариотта, Гей-Люссака, Авогадро, Дальтона.
Закон Бойля-Мариотта: При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно. Формула: pV = const
Закон Гей-Люссака:при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Формула: V/T=const
Закон Авогадро: в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул.
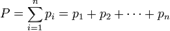
Внутренняя энергия идеального газа. Степени свободы. Теорема о равномерном распределении кинетической энергии по степеням свободы.
В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Формула:
Степени свободы — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных, необходимых для полного описания движения механической системы.
В состоянии термодинамического равновесия на каждую степень свободы движения частиц вещества приходится кинетическая энергия в среднем, равная kT/2.
Основное уравнение молекулярно-кинетической теории. Средняя кинетическая энергия молекул, молекулярно-кинетический смысл температуры.
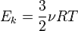
Средняя кинетическая энергия молекул:
Температура определяется через микроскопические характеристики системы и служит мерой энергии неупорядоченного движения частиц.
5. 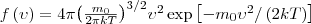
Идеальный газ в поле силы тяжести. Барометрическая формула.Распределение Больцмана.
В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.
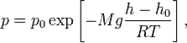
В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана:
Идеальный газ в поле силы тяжести
Каково поведение идеального газа в поле внешней силы? Для определенности в качестве внешней силы возьмем хорошо известную силу тяжести mg. Под действием внешней силы механическая система частиц приобретает импульс и перемещается как целое поступательно в направлении силы. В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.

Пусть разность давлений есть dP. Давление газа с ростом высоты уменьшается, поэтому dP равно весу слоя со знаком минус. Вес газа в объеме слоя dV = dz·S равен ρ·g·dV, где ρ — плотность газа, g — ускорение силы тяжести. Таким образом,
По определению 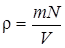
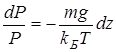
Интегрируя это соотношение, получим 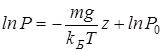
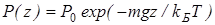
Здесь P0 — давление при z = 0. т. е. у основания столба. Аналогично с высотой изменяется и плотность частиц
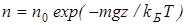
Давление и плотность газа распределены по объему газа неоднородно, они принимают максимальные значения у основания столба и убывают с высотой.
Величина, входящая в показатель экспоненты в формулах (2.9) и (2.10), есть потенциальная энергия частицы в поле тяжести U = mgz-Таким образом, распределение молекул в произвольном потенциальном внешнем поле, в котором частицы обладают потенциальной энергией U(r), может быть описано формулой:
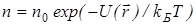
Эта формула называется распределением Больцмана. Здесь n0 — плотность частиц в точках пространства, для которых потенциальная энергия принята равной нулю.
Согласно распределению Больцмана число частиц, обладающих определенными значениями потенциальной энергии определяется отношением величины потенциальной энергии U к тепловой энергии частицы kБT. Чем больше энергия теплового движения, тем более разупорядочена система частиц, значит, тем более однородно распределены частицы в пространстве. В самом деле, если kБT >> U, 
Дата добавления: 2015-08-08 ; просмотров: 1327 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Барометрическая формула. Рассмотрим поведение идеального газа в поле силы тяжести



Рассмотрим поведение идеального газа в поле силы тяжести. Как известно, по мере подъема от поверхности Земли давление атмосферы уменьшается. Найдем зависимость давления атмосферы от высоты над уровнем моря, используя следующую упрощенную модель.
1. Температура газа и его молекулярный состав не зависят от высоты.
2. Ускорение свободного падения на всех высотах, где существует атмосфера, постоянно.
Известно, что давление жидкости высотой h на дно сосуда определяется формулой P=rgh, где r – плотность жидкости, а g – ускорение свободного падения. Эта формула справедлива, если r=const. Для жидкостей это условие хорошо выполняется, т.к. жидкость мало сжимаема. С другой стороны, для воздуха это условие нарушается, т.к. с ростом высоты r уменьшается.
Выделим на некоторой высоте h над поверхностью моря объем газа высотой dh и сечением S (рис. 8.6). Тогда давление воздуха на нижнее основание выделенного цилиндра будет
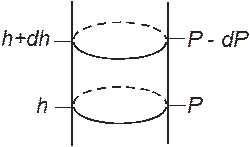 Рис. 8.6. Рис. 8.6. |
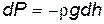 , , | (8.20) |
где r – плотность воздуха на высоте h, а знак «минус» указывает, что с ростом высоты, давление атмосферы падает.
Найдём плотность воздуха r из уравнения Менделеева–Клапейрона
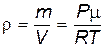 |
и подставим в (8.20). После разделения переменных получим:
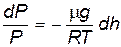 . . |
Интегрируя последнее выражение в пределах от h0 до h, получаем
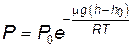 , , | (8.21) |
где P и P0 – давление атмосферы на высоте соответственно h и h0.
Последняя формула выражает зависимость давления атмосферы от высоты над уровнем моря и называется барометрической формулой.
Если в выражении (8.21) положить h0=0 (т.е. высоту отсчитывать от уровня моря), то барометрическая формула примет вид
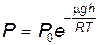 , , | (8.22) |
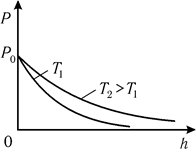 Рис. 8.7. Рис. 8.7. |
Следует отметить, что несмотря на значительное число упрощений, формула (8.22) достаточно хорошо описывает изменения атмосферного давления с высотой и применяется при определении высоты полета.
Нетрудно видеть, что при возрастании температуры зависимость P(h) будет более пологой (рис. 8.7), что может приводить к рассеиванию атмосферы на больших высотах – покиданию более быстрыми молекулами сферы притяжения данной планеты. Дальнейший анализ (8.22) позволяет также сделать ряд важных для астрономии выводов (отсутствие атмосферы на Луне вследствие малости g и т.д.).
Идеальный газ в поле силы тяжести. Барометрическая формула. Распределение Больцмана.
Макроскопическая система, макроскопические параметры. Идеальный газ, уравнение состояния идеального газа.
Макроскопические параметры – параметры значения, которых можно определить с помощью приборов, ничего не зная об атомно-молекулярном строении вещества (давление, объем, температура).
Идеальным называют газ, взаимодействием, между молекулами которого можно пренебречь.


Законы идеальных газов: Бойля-Мариотта, Гей-Люссака, Авогадро, Дальтона.
Закон Бойля-Мариотта: При постоянной температуре и массе идеального газа произведение его давления и объёма постоянно. Формула: pV = const
Закон Гей-Люссака: при постоянном давлении объём постоянной массы газа пропорционален абсолютной температуре. Формула: V/T=const
Закон Авогадро: в равных объёмах различных газов, взятых при одинаковых температуре и давлении, содержится одно и то же число молекул.

Внутренняя энергия идеального газа. Степени свободы. Теорема о равномерном распределении кинетической энергии по степеням свободы.
В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Формула:
Степени свободы — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных, необходимых для полного описания движения механической системы.
В состоянии термодинамического равновесия на каждую степень свободы движения частиц вещества приходится кинетическая энергия в среднем, равная kT/2.
Основное уравнение молекулярно-кинетической теории. Средняя кинетическая энергия молекул, молекулярно-кинетический смысл температуры.

Средняя кинетическая энергия молекул:
Температура определяется через микроскопические характеристики системы и служит мерой энергии неупорядоченного движения частиц.
5. 
Идеальный газ в поле силы тяжести. Барометрическая формула. Распределение Больцмана.
В идеальном газе, находящемся во внешнем поле сил, каждая отдельная частица приобретает импульс в направлении силы, а также соответствующую потенциальную энергию. Однако в газе наряду с упорядоченным движением в направлении действия силы существует хаотическое тепловое движение. В результате конкуренции между этими двумя типами движений возникает неравномерное распределение макроскопических параметров: плотности частиц, давления, температуры по объему, занимаемому газом.

В присутствии гравитационного поля (или, в общем случае, любого потенциального поля) на молекулы газа действует сила тяжести. В результате, концентрация молекул газа оказывается зависящей от высоты в соответствии с законом распределения Больцмана: