если целое число 101100112 записано в дополнительном коде то десятичное значение данного числа равно

Обратный и дополнительный коды двоичных чисел

Пример перевода
x₁=10101-[x₁]_пр=010101
x₂=-11101-[x₂]_пр=111101
x₃=0,101-[x₃]_пр=0,101
x₄=-0,111-[x₄]_пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение. Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.

3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.

Пример перевода
x₁=10101-[x₁]_доп=010101
x₂=-11101-[x₂]_обр=100010+1-[x₂]_доп=100011
x₃=0,101-[x₃]_доп=0,101
x₄=-0,111-[x₄]_обр=1,000+1-[x₄]_доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.

Источник

Ответ неверный

В вычислительной технике за единицу измерения информации выбрано количество информации, необходимое для различения двух равновероятных сообщений («орел-решка», «чет-нечет» и т.п.).
За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Это будет десятичная единица информации – дит.

Ответ неверный!

Термин «бод» используют для описания скорости передачи данных.
Первоначально бод использовался в телеграфии. Число бод равно количеству значащих изменений сигнала (потенциала, фазы, частоты), происходящих в секунду.
Для двоичных сигналов нередко принимают, что бод равен биту в секунду. Однако единого мнения о правильности использования этого термина нет, особенно при высоких скоростях, где число бит в секунду не совпадает с числом бод.

Ответ неверный!

Байт – единица измерения информации, равная восьми битам. Восемь бит требуется для того, чтобы закодировать любой из 256 символов основного компьютерного кода ASCII: в соответствии с формулой Р. Хартли количество информации 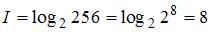(бит).

Задание 8. .

Для кодирования 20 различных состояний достаточно ________ двоичных разрядов.
5

Решение:

Позиции двоичного кода – это 0 или 1.
Воспользуемся формулой количества информации Р. Хартли: 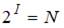, где в данном случае N – количество состояний, которые требуется закодировать, I – искомое число двоичных разрядов.
Имеем: .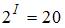
Если будем использовать 4 двоичных разряда, то сможем закодировать 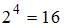различных состояний, чего недостаточно для выполнения условия задачи.
Если будем использовать 5 двоичных разрядов, то сможем закодировать 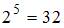различных состояния, то есть кодирование будет даже избыточным, с запасом ещё на 12 состояний.

Задание 9.

С помощью одного байта при двоичном кодировании можно представить целое неотрицательное число от нуля до…
Ответ: 255

Решение:

1 байт равен 8 битам, т.е. 8 двоичным разрядам. Количество различных однобайтовых двоичных кодов (00000000, 00000001, 00000010,…, 00110010,…, 11111111) равно 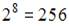. Следовательно, этими кодами можно представить 256 различных чисел, например, числа 0, 1, 2, 3,…, 255. Итак, максимальное число, которое можно представить однобайтовым двоичным кодом «11111111», равно 255.

Задание 10. .

Перевести двоичное число 1100101001101010111 в восьмеричную систему счисления.
ответ:

Задание 11.

Если 8-разрядный дополнительный код равен 10110011₂, то десятичное значение данного числа равно …

Решение:

Источник

Вопрос № 3.1. Оригинальный порядковый номер: 8

Если числа в двоичной системе счисления имеют вид 10101₂ и 1000₂, то их разность в двоичной системе счисления равна …

Вопрос № 3.2. Оригинальный порядковый номер: 13

Результат вычисления выражения 16*8 + 4*4 + 1 в двоичной системе счисления имеет вид …

Вопрос № 3.3. Оригинальный порядковый номер: 38

Вопрос № 3.4. Оригинальный порядковый номер: 42

Среди перечисленных чисел максимальным является.

Вопрос № 3.5. Оригинальный порядковый номер: 49

Среди чисел 1111101₂, 163₈, 78₁₆ превышают десятичное число 118₁₀ …

2. ни одно из чисел

Тема № 4. Кодирование данных в ЭВМ

(Задание с выбором одного правильного ответа из предложенных)

Оригинальное кол-во заданий: 17, в базе представлено: 5

Вопрос № 4.1. Оригинальный порядковый номер: 7

Вопрос № 4.2. Оригинальный порядковый номер: 9

Вопрос № 4.3. Оригинальный порядковый номер: 11

Дополнительный код числа 4₁₀ в однобайтовом формате имеет вид.

Вопрос № 4.4. Оригинальный порядковый номер: 13

Дополнительный код числа 1₁₀ в однобайтовом формате имеет вид.

Вопрос № 4.5. Оригинальный порядковый номер: 16

При байтовом кодировании алфавита максимальная мощность алфавита составляет ________ символов(а).

Тема № 5. Основные понятия алгебры логики

(Задание с выбором одного правильного ответа из предложенных)

Оригинальное кол-во заданий: 56, в базе представлено: 5

Вопрос № 5.1. Оригинальный порядковый номер: 1

Выполните подстановку операции так, чтобы равенство (1 OR 0) ________ 0 = 0 оказалось верным (здесь OR – логическое ИЛИ).

1. логическое ИЛИ (OR)

3. логическое И (AND)

4. исключающее ИЛИ (XOR)

Вопрос № 5.2. Оригинальный порядковый номер: 3

Выполните подстановку операции так, чтобы равенство (1 AND 0) ________ 1 = 0 оказалось верным (здесь AND – логическое И).

1. логическое ИЛИ (OR)

3. логическое И (AND)

4. исключающее ИЛИ (XOR)

Вопрос № 5.3. Оригинальный порядковый номер: 16

Приоритеты выполнения операций в логическом выражении в порядке убывания:

1. дизъюнкция, инверсия, конъюнкция, импликация

2. импликация, инверсия, конъюнкция, дизъюнкция

3. инверсия, конъюнкция, дизъюнкция, импликация

4. конъюнкция, инверсия, дизъюнкция, импликация

Вопрос № 5.4. Оригинальный порядковый номер: 31

1. A=1, B=0, C=1

2. A=0, B=0, C=0

3. A=0, B=0, C=1

4. A=1, B=1, C=1

Вопрос № 5.5. Оригинальный порядковый номер: 47

Для того, чтобы логическое выражение

при любых значениях логических переменных a и b всегда принимало значение “истина”, вместо знака вопроса…

1. можно поставить знак конъюнкции ( ), но не знак дизъюнкции ( )

2. можно поставить как знак дизъюнкции( ), так и знак конъюнкции( )

3. нельзя поставить ни знак дизъюнкции ( ), ни знак конъюнкции ( )

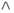
4. можно поставить знак дизъюнкции ( ), но не знак конъюнкции ( )

Источник

Прямой, обратный и дополнительный коды двоичного числа

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

Прямой код

Обратный код

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

Арифметические операции с отрицательными числами в обратном коде:

Дополнительный код

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Арифметические операции с отрицательными числами в дополнительном коде

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

(35 голосов, оценка: 4,69 из 5)

Источник

Прямой, дополнительный и обратный коды

Прямой, дополнительный и обратный код числа (создан по запросу).

Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.

Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.

Прямой, дополнительный и обратный код

Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен

Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.

Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица

А теперь «зачем, зачем это все?» ©

Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.

С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111

А как представить отрицательные числа?

И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)

Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4

-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6

Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.

Примеры где показаны переносы и пятый разряд

00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение

Два последних переноса 01 — переполнение

-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0

Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.

Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.

Источник