два разряда двоичного кода содержат сколько бит
Двоичная система счисления
Двоичный код — понятие, которое кажется сложным большинству людей. Однако на самом деле это одна из самых простых шифровальных систем в мире. Более того, мы сталкиваемся с ней ежедневно в обычной жизни.
Например, в наших компьютерах хранится самая различная информация — текстовые файлы, видеоролики, аудиозаписи и изображения. Но в виде картинок, текстов и мультимедийных файлов эту информацию видим только мы — а сам компьютер воспринимает и обрабатывает любые сведения в форме двоичного кода.
Двоичная система счисления — что это такое?
Двоичный, или, как еще его называют, бинарный код — шифр, состоящий всего из двух символов. Его можно сравнить с азбукой Морзе, где используются только тире и точки в разных комбинациях — морзянкой передают сколь угодно сложные сообщения.
Двоичный код чаще всего представлен нулем и единицей. Но это не обязательно — двоичного кода можно брать и любые другие обозначения, главное, чтобы эти символы были противоположными или взаимоисключающими по сути.
Что такое разрядность двоичного кода?
Одним из важных свойств двоичной системы является понятие разрядности — этим словом называют количество позиций, используемых в конкретном коде для составления комбинаций.
Смысл разрядного двоичного кода заключается в том, что одно и то же число в нем можно обозначить разными комбинациями символов — например, обозначения 0001, 001, 01 и 1 будут подразумевать одно и то же число «1». Читают разряды не так, как текст, а справа налево. Как правило, на практике код бывает 4, 8, 16, 32 и 64 разрядным — в зависимости от объема информации и специфики решаемой задачи.
У неопытного пользователя может возникнуть вопрос — какой смысл в двоичной системе, и не проще ли обходиться без нее? Однако когда речь идет о сложной вычислительной технике, то оперировать огромным множеством простейших элементов для нее удобнее, нежели обращаться с малочисленными, но сложными символами.
Два разряда двоичного кода содержат сколько бит
Информация и её двоичное кодирование
Информация является ключевым понятием в курсе информатики. Слово information латинского происхождения и означает сведение, разъяснение, ознакомление. Можно выделить несколько подходов к определению этого понятия.
В быту слово применяется как «сведения», «сообщения», «осведомления о положении дел».
В кибернетике (науке об управлении) слово используется для характеристики управляющих сигналов.
В философии это понятие тесно связано с таким понятием как «взаимодействие» и «познание».
В информатике понятие «информация» вводится как мера уменьшения неопределённости. Такой подход позволяет количественно измерять информацию.
æ За единицу количества информации принята информация, которая посылает в компьютер один электрический сигнал в виде числа 1 или 0. Такая единица информации названа бит.
Количество двоичных различных чисел можно определить по формуле:
11110000 – код 8-ми разрядный
n = 8, количество таких кодов N = 2 8 = 256,
1. Что принято за единицу измерения количества информации?
2. Какое количество информации несёт один разряд двоичного числа? Два разряда? Три разряда?
3. Какое количество двоичных чисел можно записать с помощью четырёхразрядных кодов?
4. Какое количество кодов используется при кодировании информации 16-, 32- разрядной ЭВМ.
5. При кодировании цвета используют 4- разрядные коды, какое количество цветов при настройке ПК предлагается пользователю?
6. Оттенки цветовой гаммы True Color кодируются 16777216 кодами. Какой разрядности коды используются?
1. Единицы измерения количества информации.
В информатике наиболее употребляемой единицей измерения количества информации является байт, причём 1 байт = 8 бит Компьютер оперирует двоичной системой счисления, поэтому в кратных единицах измерения используется коэффициент 2 10 = 1024.
1 Кбайт = 2 10 байт = 1024 байта
1 Мбайт = 2 10 Кбайт = 1024 Кбайт
1 Гбайт = 2 10 Мбайт = 1024 Мбайт
1. С помощью стандартной программы Windows Калькулятор вычислите:
· Сколько бит в одном килобайте?;
· Сколько байт в одном Гигабайте?
2. Заполните таблицу. Вычисления выполнить с помощью приложения Калькулятор, ответ записать с точностью до сотых.
Гибкий магнитный диск (3,5 дюйм)
3. Сколько страниц формата А4, полностью записанных, можно сохранить на гибком диске, объёмом памяти 1,38 Мбайт?
4. Можно ли 30 страниц курсового проекта сохранить в памяти на жёстком диске вашего компьютера?
2. Двоичное кодирование информации.
Компьютер может обрабатывать числовую, текстовую, графическую, звуковую и видео информацию.
Все виды информации кодируются в последовательности электрических импульсов, т.е. в последовательность нулей и единиц.
Числовую информацию компьютер обрабатывается двоичной системе счисления. Таким образом, числа в компьютере представлены в виде последовательности нулей и единиц (0, 1) или битов. Восьми разрядная ЭВМ может обрабатывать максимальное число – 11111111 2 (вычислите какому числу в десятичной системе счисления соответствует данное двоичное число).
В настоящее время большая часть ПК занято обработкой текстовой информацией.
æ При двоичном кодировании текстовой информации каждому символу ставится в соответствии своя уникальная последовательность из 0 и 1, свой уникальный двоичный код от 00000000 до 11111111 (десятичный код от 0 до 255).
Графическая информация на экране монитора представлена в виде изображения, которое формируется из (пикселей) точек. Чёрно-белое изображение без градаций серого цвета может иметь два состояния – «черная» или «белая». Для хранения состояния необходим 1бит.
Цветные изображения могут иметь различную глубину цвета (бит на точку: 4, 8, 16, 24).
Количество отображаемых цветов (N)
æ Графический режим вывода изображения на экран определяется разрешающей способностью экрана и глубиной цвета. Полная информация обо всех точках, хранящихся в видеопамяти, называется битовой картой изображения.
Современные компьютеры обладают такими техническими характеристиками, которые позволяют обрабатывать и выводить на экран, так называемое «живое видео», т.е. видеоизображение естественных объектов. Видео формируется из отдельных кадров. Частота кадров 25 герц, т.е. за одну секунду сменяется 25 кадров.
С начала 90-х годов ЭВМ получили возможность работать со звуковой информацией. Звуковой сигнал – это непрерывная волна с изменяющейся амплитудой и частотой. Непрерывный звуковой сигнал превращают в последовательность электрических сигналов.
Современные звуковые карты могут обеспечить кодирование 65536 различных уровней сигнала или состояний, обеспечивают 16 – битное кодирование звука. При каждой выборке значении амплитуды звукового сигнала присваивается 16 – битный код.
2. Какое максимальное число в десятизначной системе счисления может обрабатывать 16 – разрядная ЭВМ?
3. Как кодируются символы текста?
4. Используя Таблицу символов, запишите последовательность десятичных числовых кодов в кодировке Windows ( CP 1251) для слова компьютер.
5. Используя Блокнот, определите какие слова в кодировке Windows ( CP 1251) заданы последовательностью числовых кодов:
· 11011101, 11000010, 11001100.
6. Закодируйте двоичными кодами своё полное имя, используя Таблицу символов и Блокнот.
7. Найдите объём видеопамяти для различных графических режимов. Заполните таблицу.
Бит | Байт | Системы счисления
Для полноты понимания работы микроконтроллера необходимо четко знать, что такое бит и байт, а также уметь применять различные системы счисления.
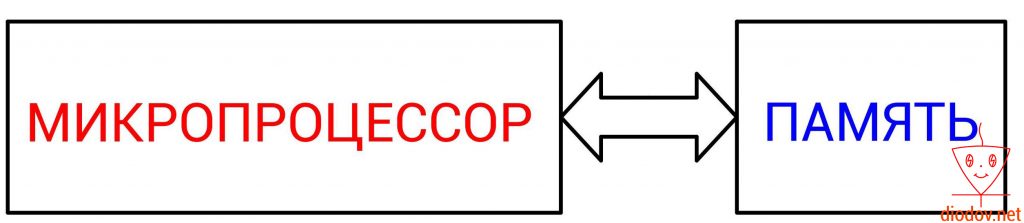
Основным вычислительным ядром любого микроконтроллера является микропроцессор. Именно он выполняет обработку команд или же кода, написанного программистом.
Упрощенно работу микропроцессора можно представить следующим образом. Сначала выполняется считывание данных из определенной ячейки памяти, далее выполняется их обработка и затем возвращение результата назад в ячейку памяти. Следовательно, для того, чтобы микропроцессор мог выполнять свои функции необходимо наличие памяти. Иначе ему неоткуда будет считывать данные, а затем некуда помещать результаты вычислений.
Давайте кратко рассмотрим алгоритм работы микропроцессора (МП) на примере сложения двух цифр.
Вот такой монотонной работой занимаются микропроцессоры. Для выполнения одной команды ему необходимо выполнить четыре операции. Однако современные МП выполняют более 1 000 000 000 операций за одну секунду. Микроконтроллеры же выполняют более 1 000 000 операций, чего, как правило, предостаточно для такого крохотного устройства.
Данные, с которыми оперирует микропроцессор, представляют собой набор цифр. Поэтому нашей целью является рассмотреть, какие цифры, а точнее системы счисления “понимает” микроконтроллер.
Десятичная система счисления
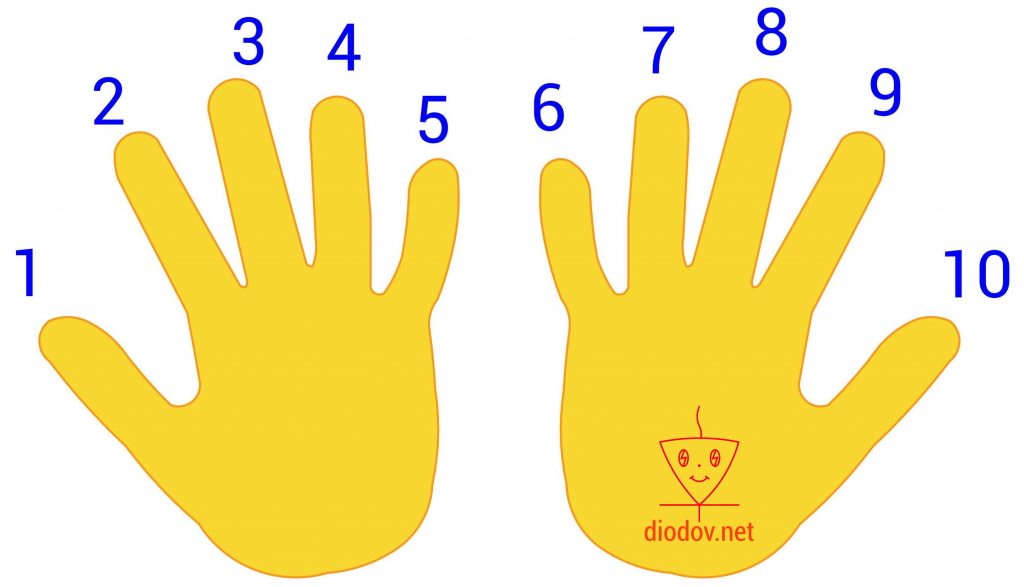
Десятичная система счисления нам очень близка и понятна. Возникла она очень давно, когда у людей впервые возникал необходимость подсчета чего-либо, например количества дней или определённых событий. Поскольку в те давние времена не было каких-либо технических устройств, то люди использовали для счета пальцы рук. Загибая или разгибая пальцы можно получить десять комбинаций, что очень просто и наглядно.
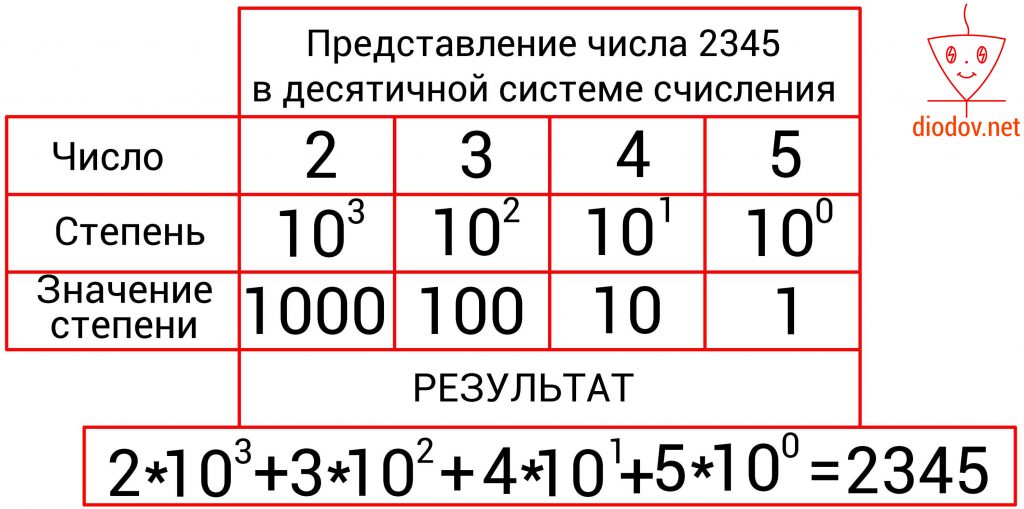
Математически данная она состоит из десяти разных символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, поэтому она и называется десятичной. С помощью указанных символов легко отобразить любое число.
Основанием десятичной системы является 10. Когда при счете использованы все знаки от 0 до 9, то, чтобы продолжить дальнейший счет, необходимо вместо символа 9 поставить символ 0, т. е. обнулить предыдущее значение, а слева от нуля записать символ 1. И так можно продолжать счет до бесконечности, прибавляя слева от текущей позиции цифры последующую.
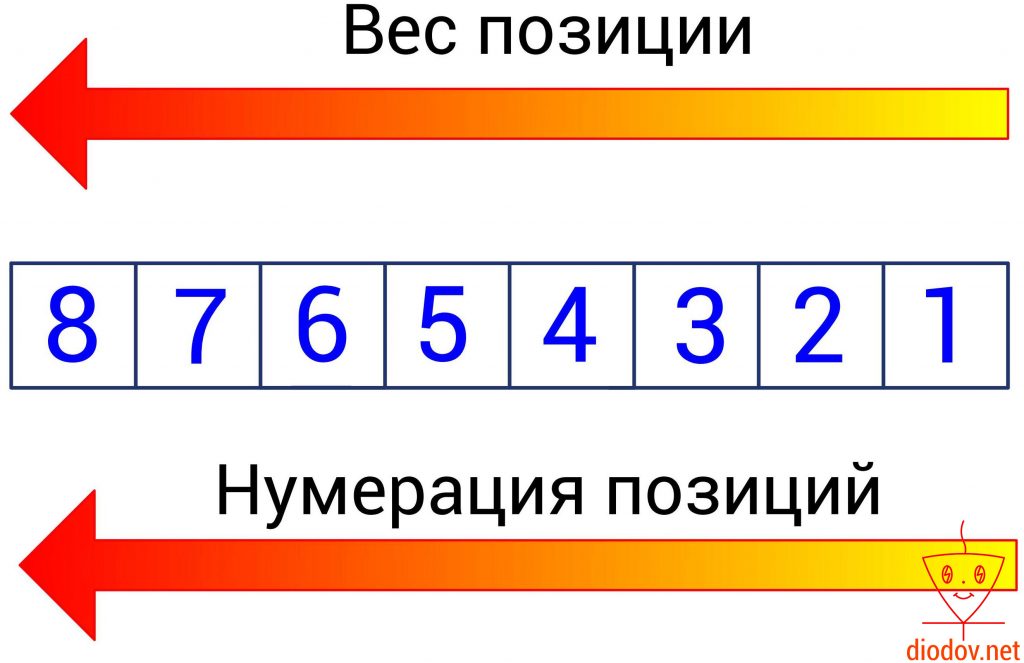
Каждая позиция цифры имеет свой вес. Наименьший вес имеет позиции, находящаяся в крайнем правом положении. По мере перемещения слева на право, вес позиции возрастает.
Например, число 2345 имеет 4 позиции. В крайней левой позиции отображаются единицы, в данном случае 5 единиц, а степень 10 имеет нулевое значение. Далее вес позиции увеличивается. Следующее значение, расположенное слева от предыдущего, уже содержит десятки, а 10 имеет степень 1, поэтому во второй позиции числа 2345 четыре десятка.
Двоичная система счисления
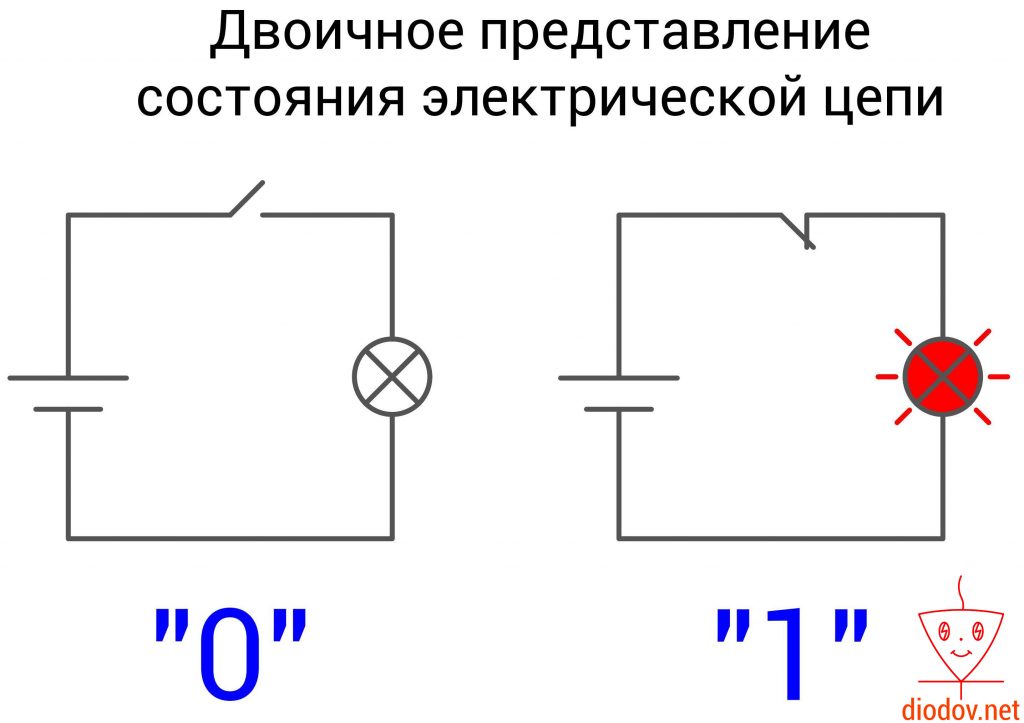
Двоичная система счисления оперирует всего лишь двумя символами 0 и 1. Она повсеместно применяется в цифровой технике, поскольку очень удачно сочетается с двумя устойчивыми состояниями электрической цепей: включено и выключено либо есть сигнал и нет сигнала. Также нулем еще обозначают сигнал низкого уровня, а единицей – высокого.
Порядок записи двоичного числа полностью соответствует десятичному. Веса позиций также возрастают справа налево. Только основанием является 2, а не 10.
Чтобы отличать двоичную систему от десятичной в цифровой технике используют индекс 2 и 10 соответственно:
110110 – десятичное.
При написании кода программы для обозначения двоичного значения перед ним ставится префикс 0b, например 0b11010101. Если записывается десятичное, то перед ним ничего не ставится.
0b11010101 – двоичное;
11010101 – десятичное.
Бит и байт
Двоичная система счисления также используется при хранении и обработке информации.
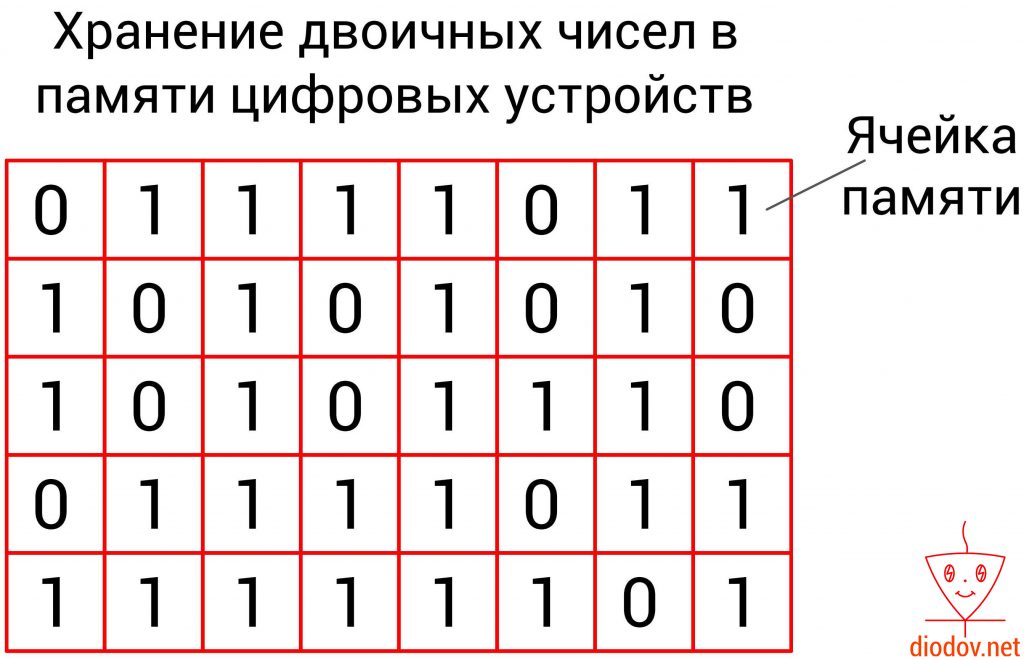
Вся информация цифровых запоминающих устройств хранится в памяти. Память представляет собой набор ячеек.
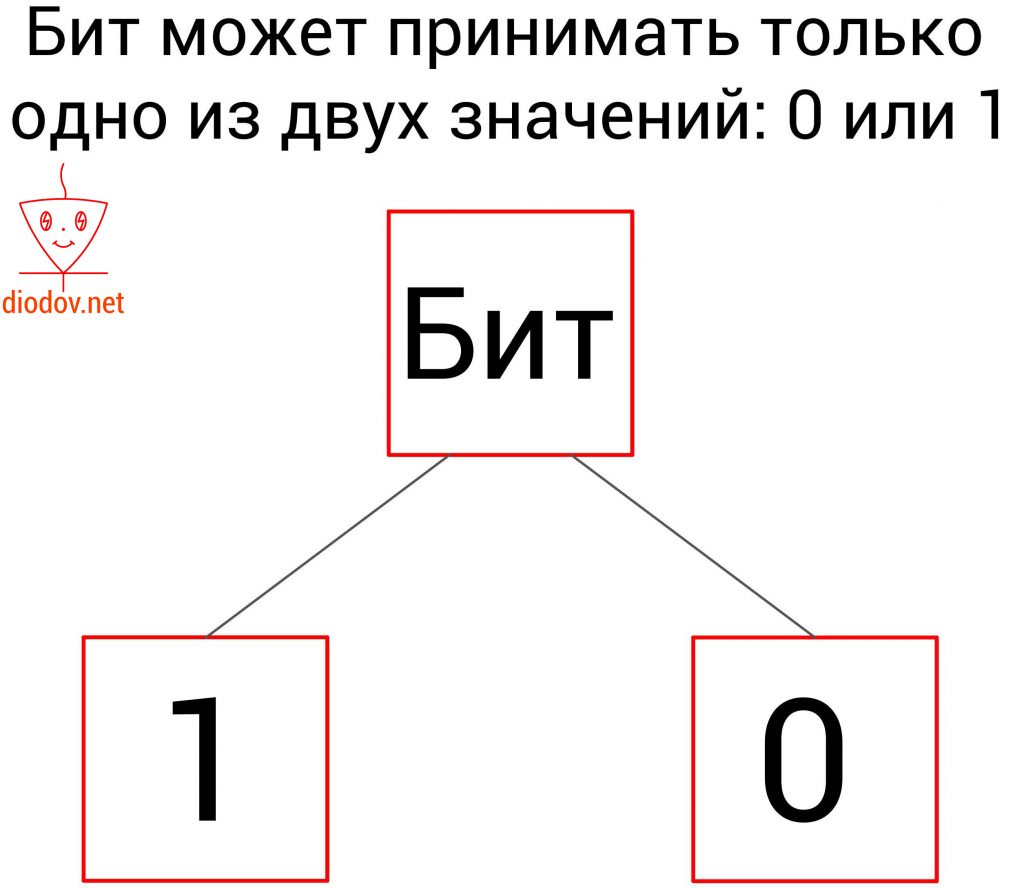
Каждая ячейка содержит один бит данных. Бит – это единица измерения объема памяти. В одном бите можно запоминать максимум два значения: 0 – это одно значение, а 1 – второе.
Bit происходит от двух английских слов Binary Digit (двоичное число).
При работе с битами регистров микроконтроллера мы будем часто обращаться к таким понятиям, как старший и младший биты. Эти понятия строго регламентированы. В двоичной системе разряд, который имеет самую правую позицию, получил название младший значащий бит (МЗБ). В англоязычной литературе его называют Least Significant Bit (LSB). Именно с него начинается нумерация битов.
Наибольший вес имеет бит, находящийся в самой левой ячейке памяти. Его принято называть старший значащий бит (СЗБ) или Most Significant Bit – MSB.
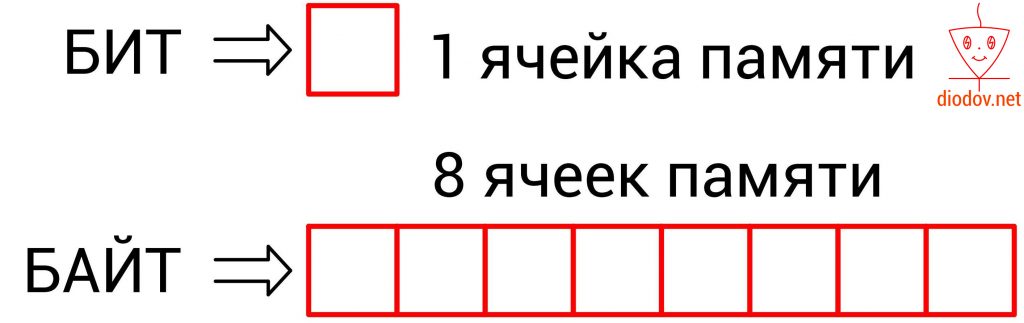
Более емкой единицей информации является байт (byte). Он равен 8 битам, т. е. восемь элементарных ячеек памяти составляют один байт.
1 байт = 8 бит
В одном бите можно хранить только два разных значения или две комбинации. А в 1 байте можно хранить 256 различных комбинаций. Ровно столько же символов содержится в таблице кодировки ASCII. Но об этом в другой раз.
На практике пользуются большими значениями объёма памяти килобайтами, мегабайтами, гигабайтами и терабайтами.
1 килобайт (кБ) = 1024 байт
1 мегабайт (МБ) = 1024 кБ
1 гигабайт (ГБ) = 1024 МБ
1 терабайт (ТБ) = 1024 ГБ
Преобразование десятичного числа в двоичное
На практике программисты часто пользуются несколькими системами счисления. Поэтому следует научиться переводить числа из десятичной системы в двоичную. Здесь можно выделить два простых способа. Рассмотрим их по порядку.
Первый способ заключается в том, что десятичное число непрерывно делится на два. При этом учитывается полностью ли оно разделилось или с остатком. Если значение делится без остатка, как например 4/2 = ровно 2 или 6/2 = ровно 3, то записывается ноль, а если с остатком, как 3/2 или 5/2, то записывается единица.
Теперь давайте переведем число 125 в двоичную форму.
125/2 = 62 остаток 1
Получаем двоичное число 11111012
Я надеюсь здесь понятно, что если 1 разделить на 2, то математически ноль никак не получится, однако такой подход позволяет объяснить данный алгоритм.
Второй способ
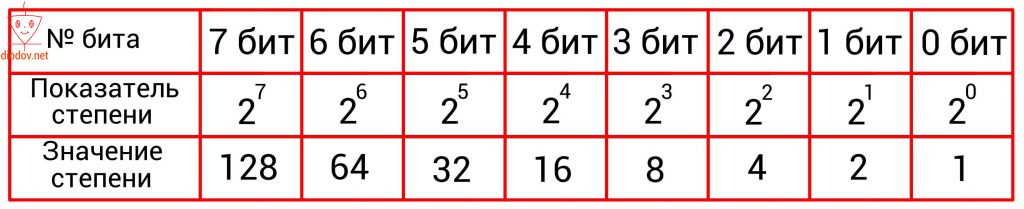
Второй способ имеет такую идею. С изначального числа нужно вычесть число в степени два, которое будет меньше заданного значения. Для ускорения процесса преобразования воспользуемся следующей таблицей.
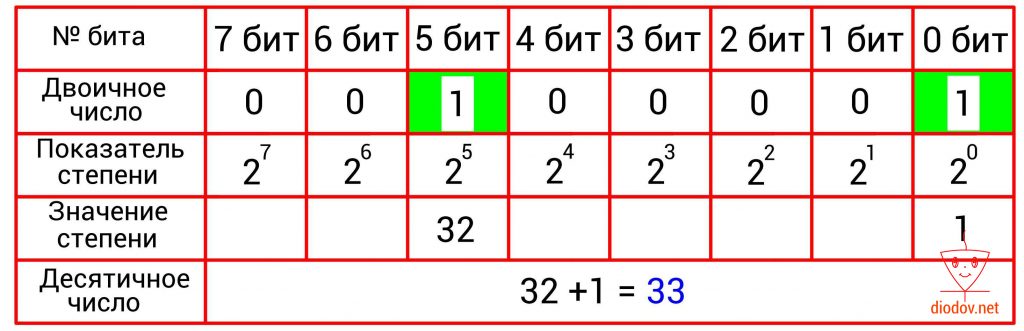
Давайте преобразуем 125.
Следует обратить особое внимание на то, что нумерация битов, во-первых, выполняется справа налево, а во-вторых начинается с нуля! Это несколько непривычно, поскольку в десятичной системе счисления счет принято начинать с единицы. Однако в цифровой технике счет всегда идет с нуля! К этому следует приучить себя заранее, так как при написании программ для микроконтроллеров мы все время будем начинать счет битов с нуля. В дальнейшем вы такому счету быстро привыкнете, поскольку и в техническом описании МК строго соблюдается данное правило.
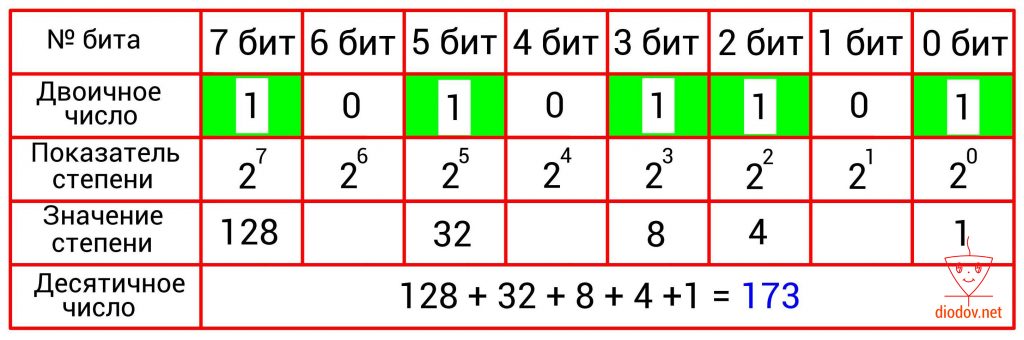
Преобразование двоичного числа в десятичное
Преобразование двоичного числа в десятичное выполняется довольно просто. Для этого следует сложить десятичные веса всех двоичных разрядов, в которых имеются единицы. Биты, в которых записан ноль, пропускаются. В качестве примера возьмем такое значение: 10101101. Нулевой, второй, третий, пятый и седьмой биты имеют единицы. Получаем: 2 0 + 2 2 + 2 3 + 2 5 + 2 7 = 1 + 4 +8 + 32 + 128 = 173.
В таблицах, приведенных ниже, наглядно показано перевод чисел из двоичной в десятичную систему счисления.
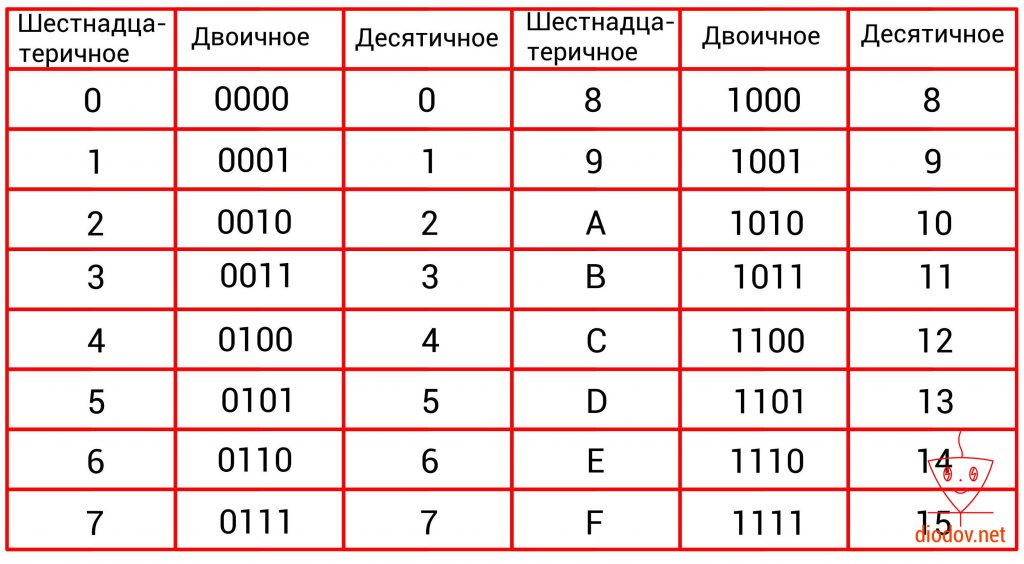
Шестнадцатеричная система счисления
В программировании микроконтроллеров очень часто пользуются шестнадцатеричными числами. Данная система счисления имеет основание 16, соответственно и 16 различных символов. Первые десять символов 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 заимствованы из десятеричной системы. В качестве оставшихся шести символов применяются буквы A, B, C, D, E, F.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Высокая популярность шестнадцатеричной системы счисления поясняется тем, что при отображении одного и того же значения используется меньше разрядов по сравнению с десятичной системой и тем более с двоичной. Например, при отображении 100 используется три десятичных разряда 10010 или 7 двоичных разрядов 11001002 и только 2 шестнадцатеричных разряда 6416.
А если записать 1000000, то разница в количестве занимаемых разрядов буде еще более ощутима:
1 000 00010 = 1111 0100 0010 0100 00002 = F424016
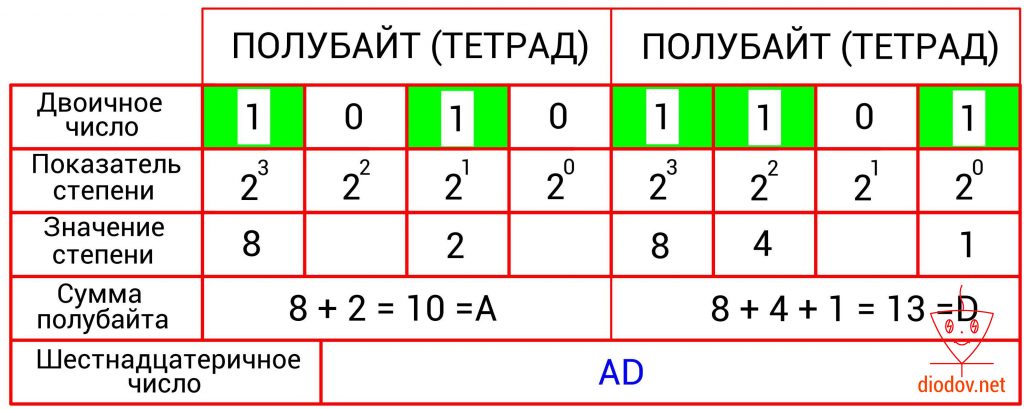
Преобразование двоичного числа в шестнадцатеричное
Еще одним положительным свойством шестнадцатеричного числа является простота получение его из двоичного. Такое преобразование выполняется следующим образом: сначала двоичное число разбивается на группы по четыре быта или на полубайты, которые еще называют тетрадами. Если количество битов не кратно четырем, то их дополняют нулями. Далее следует сложить значение всех битов в каждом полубайте. Сумма каждого полубайта даст значение отдельной цифры шестнадцатеричного числа.
Другие системы счисления
В цифровой технике также применяется восьмеричная система счисления, но она не нашла применения в микроконтроллерах.
Теоретические можно получить бесконечное значение систем счисления: троичную, пятиричную и даже сторичную, т.е. с любым основанием. Однако практической необходимости в этом пока что нет.
Наиболее простой и быстрый способ преобразования чисел с одной системы счисления в другую – это применение встроенного в операционную систему калькулятора. Найти его можно следующим образом: Пуск – Все программы – Стандартные – Калькулятор.
Чтобы перейти в «нужный» режим следует кликнуть по вкладке Вид и выбрать Программист или нажать комбинацию клавиш Alt+3.
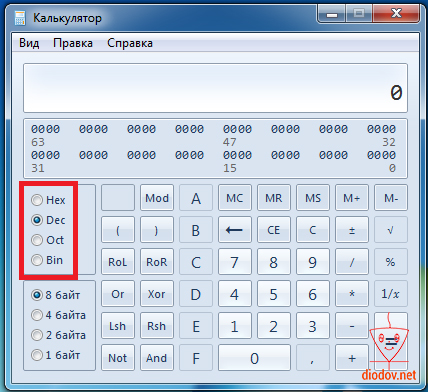
В открывшемся окне можно вводить двоичные, восьмеричные, шестнадцатеричные и десятичные числа, выбрав соответствующий режим. Кроме того можно выполнять различные математические операции между ними.
В дальнейшем, при написании кода программы мы часто будем обращаться к данному калькулятору. Кроме того, опытные программисты любят использовать шестнадцатеричные числа, а нам проще будет понять двоичный код, поэтому калькулятор в помощь)
Двоичный код
Двоичный код — это способ представления данных в одном разряде в виде комбинации двух знаков, обычно обозначаемых цифрами 0 и 1. Разряд в этом случае называется двоичным разрядом.
В случае обозначения цифрами «0» и «1», возможные состояния двоичного разряда наделяются качественным соотношением «1» > «0» и количественными значениями чисел «0» и «1».
Двоичный код может быть непозиционным и позиционным.
Из комбинаторики известно, что, в случае непозиционного кода, количество комбинаций (кодов) n-разрядного кода является числом сочетаний с повторениями, равно биномиальному коэффициенту:



В двоичной системе кодирования (n=2) количество возможных состояний (кодов) равно :



Например, в одном 8-ми битном байте (k=8) количество возможных состояний (кодов) равно:

В случае позиционного кода, число комбинаций (кодов) n-разрядного двоичного кода равно числу размещений с повторениями:


Используя два двоичных разряда можно закодировать четыре различные комбинации: 00 01 10 11, три двоичных разряда — восемь: 000 001 010 011 100 101 110 111, и так далее.
При увеличении разрядности позиционного двоичного кода на 1, количество различных комбинаций в позиционном двоичном коде удваивается.
Двоичные коды являются комбинациями двух элементов и не являются двоичной системой счисления, но используются в ней как основа. Двоичный код также может использоваться для кодирования чисел в системах счисления с любым другим основанием. Пример: в двоично-десятичном кодировании (BCD) используется двоичный код для кодирования чисел в десятичной системе счисления.
При кодировании алфавитноцифровых символов (знаков) двоичному коду не приписываются весовые коэффициенты, как это делается в системах счисления, в которых двоичный код используется для представления чисел, а используется только порядковый номер кода из множества размещений с повторениями.
В системах счисления n-разрядный двоичный код, (n-1)-разрядный двоичный код, (n-2)-разрядный двоичный код и т. д. могут отображать одно и то же число. Например, 0001, 001, 01, 1 — одно и то же число — «1» в двоичных кодах с разным числом разрядов — n.
Содержание
Таблица двоичных кодов
Пример «доисторического» использования кодов
Инки имели свою счётную систему кипу, которая физически представляла собой верёвочные сплетения и узелки. Генри Эртан обнаружил, что в узелках заложен некий код, более всего похожий на двоичную систему счисления. [1]
Примечания
См. также
Полезное
Смотреть что такое «Двоичный код» в других словарях:
двоичный код — Код, основание которого равно двум. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] Тематики теория передачи информации EN binary code … Справочник технического переводчика
двоичный код — dvejetainis kodas statusas T sritis automatika atitikmenys: angl. binary code vok. binärer Kode, m; Binärkode, m; dualer Kode, m; Dualkode, m rus. двоичный код, m pranc. code binaire, m … Automatikos terminų žodynas
двоичный код — Код, основание которого равно двум … Политехнический терминологический толковый словарь
двоичный код с исправлением ошибок — Двоичный код, избыточность которого обеспечивает автоматическое обнаружение и исправление ошибок некоторых типов в передаваемых данных. [Домарев В.В. Безопасность информационных технологий. Системный подход.] Тематики защита информации EN вinаry… … Справочник технического переводчика
двоичный код с обнаружением ошибок — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN binary error detecting code … Справочник технического переводчика
Двоичный код Голея — У этого термина существуют и другие значения, см. Код Голея. Двоичный код Голея один из двух тесно связанных друг с другом исправляющих ошибки линейных кодов: совершенный двоичный код Голея (англ. perfect binary Golay code) … … Википедия
арифметический двоичный код — обычный двоичный код — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы обычный двоичный код EN natural binary code … Справочник технического переводчика
натуральный двоичный код ИКМ — Код, при котором кодовые слова, соответствующие квантованным отсчетам сигнала электросвязи при ИКМ, расположенным в порядке возрастания амплитуд, представляют собой неотрицательные целые двоичные числа, взятые в том же порядке. [ГОСТ 22670 77]… … Справочник технического переводчика
сбалансированный двоичный код — код без преобладания — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы код без преобладания EN zero disparity code … Справочник технического переводчика
симметричный двоичный код ИКМ — Код, при котором полярность квантованного отсчета сигнала электросвязи при ИКМ выражается одним символом цифрового сигнала электросвязи, а остальные символы выражают двоичное число, представляющее абсолютную величину отсчета этого сигнала.… … Справочник технического переводчика