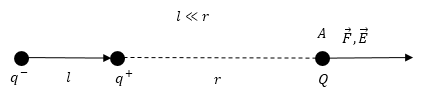диполь в однородном поле

3.1.1. Диполь в однородном электрическом поле

При внесении электрического диполя в однородное внешнее электрическое поле на каждый из его зарядов со стороны поля будут действовать равные по величине, но противоположные по направлению силы:

.

Силы создают вращающий момент:

или , (3.4)

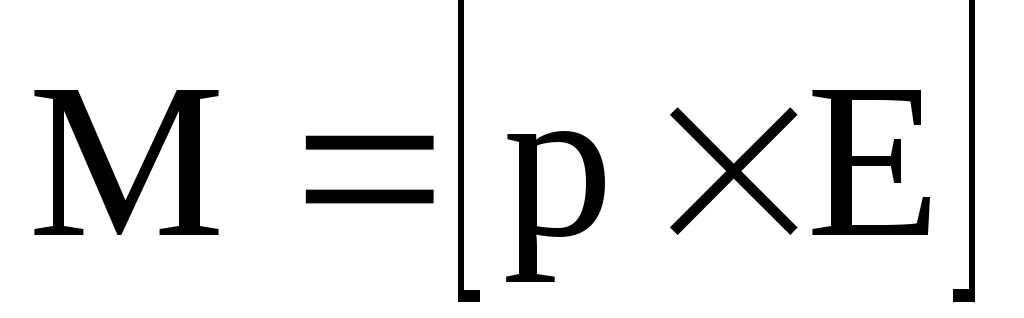
который будет стремиться повернуть диполь так, чтобы его электрический дипольный момент был направлен по направлению внешнего электрического поля (рис. 3.2).

3.1.2. Диполь в неоднородном внешнем электрическом поле

Если диполь помещен в неоднородное внешнее электрическое поле, то силы, действующие на заряды q₊ и q_—, не равны по величине и направлению, так как напряженность электрического поля в точках расположения зарядов не одинакова по величине, отличается на величину

, (3.5)

В этом случае на отрицательный заряд действует сила

.

На положительный заряд действует сила

.

Результирующая сила, действующая на диполь,

(3.6)

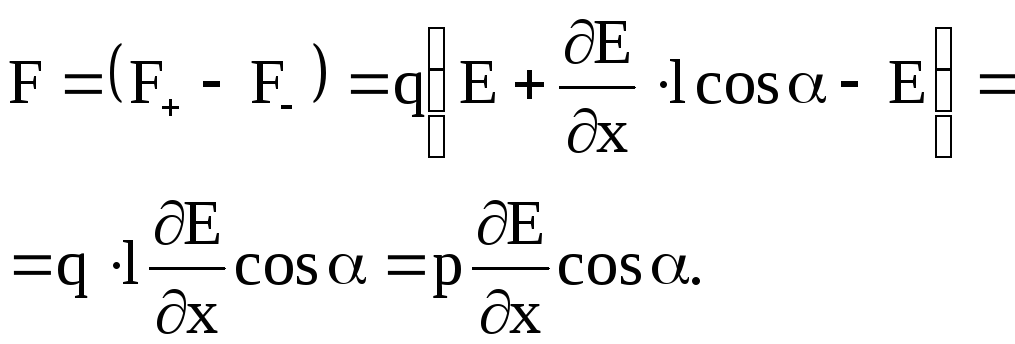
Под действием этой силы диполь будет либо втягиваться в область более сильного поля (), либо выталкиваться из него () (рис. 3.4).

Такое же действие оказывает электрическое поле на молекулы диэлектрика.

3.2. Свободные и связанные (поляризационные) заряды в диэлектриках. Поляризация диэлектриков. Вектор поляризации (поляризованность)

Процесс «появления» зарядов на диэлектриках во внешнем электрическом поле называют поляризацией диэлектрика. «Появившиеся» заряды называют связанными (поляризационными).

Различные вещества поляризуются по-разному в зависимости от их строения. Наиболее часто встречаются следующие виды поляризации диэлектриков:

а) деформационная поляризация – это поляризация диэлектриков, при которой у атомов возникает (индуцируется) дипольный момент за счет деформации электронных орбит. Наблюдается у диэлектриков, состоящих из неполярных молекул у веществ, молекулы которых имеют симметричное строение (N₂, H₂, O₂, CO_2, CH₄);

б) ориентационная, или дипольная поляризация, которая заключается в ориентации имеющихся дипольных моментов молекул по направлению электрического поля. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрического поля и теплового движения) возникает преимущественная ориентация дипольных моментов по полю. Ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура. Она характерна для диэлектриков, состоящих из полярных молекул веществ, молекулы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. К таким веществам, например, относятся H₂O, NH₃, SO₂, CO;

При помещении диэлектрика во внешнее электрическое поле он поляризуется, т.е. приобретает отличный от нуля электрический дипольный момент:

, (3.7)

где p_i – дипольный момент одной молекулы.

Для количественной характеристики поляризации диэлектриков вводится в рассмотрение физическая величина, численно равная электрическому дипольному моменту единицы объема диэлектрика:

. (3.8)

Эта величина называется вектором поляризации, или поляризованностью. Если поле или диэлектрик однородны, то вектор поляризации одинаков по всему объему. Такую поляризацию называют однородной. Если эти условия не выполняются, то поляризацию называют неоднородной.

У большинства диэлектриков, кроме так называемых сегнетоэлектриков, вектор поляризации пропорционален напряженности внешнего электрического поля:

, (3.9)

где  – диэлектрическая восприимчивость вещества, не зависящая от напряженности внешнего электрического поля.

Между вектором поляризации P и поверхностной плотностью связанных зарядов  ‘ имеется связь

, (3.10)

т. е. поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности диэлектрика.

Внутри диэлектрика в этом случае существует результирующее электрическое поле с напряженностью

, (3.14)

где – напряженность внешнего электрического поля;

–напряженность электрического поля связанных зарядов.

. (3.15)

Вне диэлектрика напряженность внешнего поля равна напряженности результирующего электрического поля.

Так как поле перпендикулярно граням пластины и плоскостям, то E_n = E, а с учетом того, что 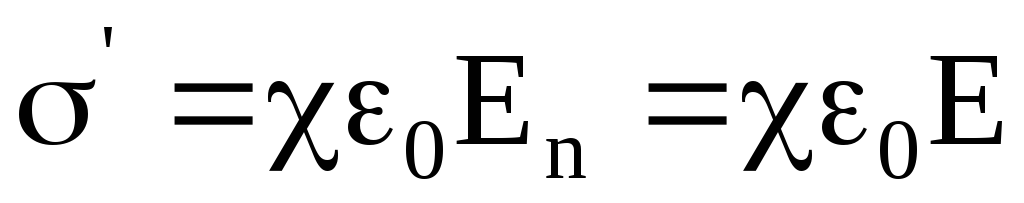, выражение (3.15) можно переписать так:

. (3.16)

Из формулы (3.16) имеем

,

,

. (3.17)

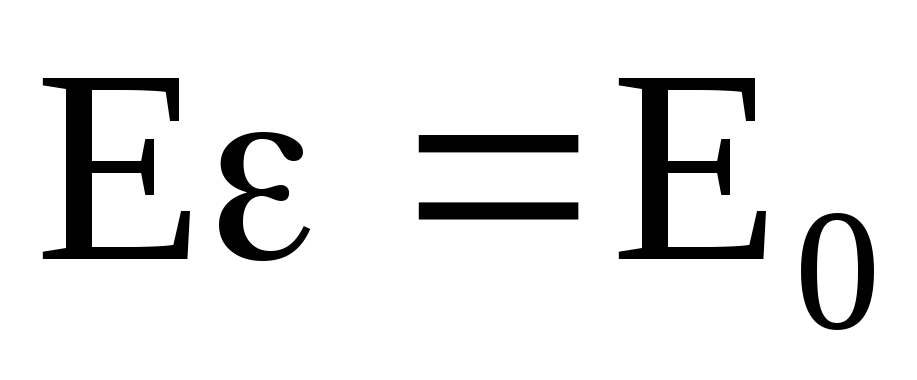
Следовательно, относительная диэлектрическая проницаемость среды показывает, во сколько раз электрическое поле ослабевает за счет диэлектрика.

Индукция электрического поля D внутри диэлектрика и вне диэлектрика одинакова, т.к. при умножении на₀ имеем

, или , (3.18)

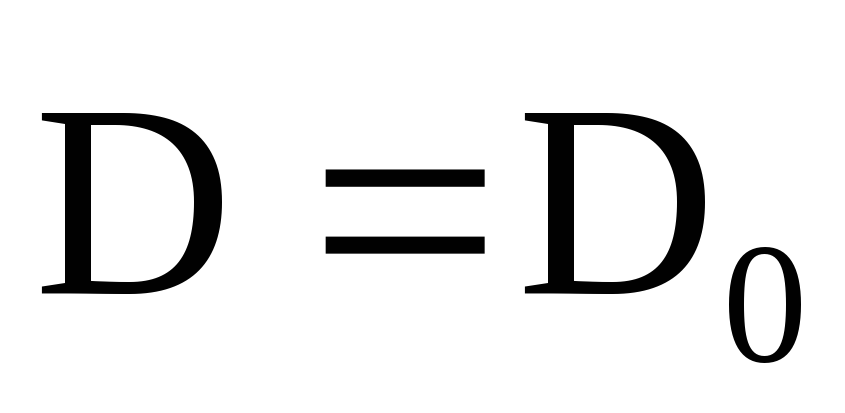
где D = ₀E – индукция (электрическое смещение) электрического поля внутри диэлектрика;

D_o = ₀E – индукция (электрическое смещение) электрического поля вне диэлектрика.

Таким образом, индукция электрического поля в диэлектрике изменяет свое направление, но не изменяет свою величину, в то время как напряженность электрического поля E  E_o. Полученный результат справедлив для любых электрических полей.

Следовательно, на границе раздела двух сред происходит изменение вектора напряженности электрического поля E (уменьшается число силовых линий вектора E), а вектор индукции электрического поля не изменяется (изменяется лишь вид силовых линий вектора D). Отсюда вывод: поток вектора индукции электрического поля через любую замкнутую поверхность остается величиной постоянной.

Для потока вектора индукции электрического поля D справедлива теорема Остроградского-Гаусса: поток вектора индукции электрического поля через любую замкнутую поверхность равен алгебраической сумме электрических зарядов, заключенных внутри этой замкнутой поверхности.

Математически эту теорему можно записать так:

. (3.19)

Источник

3.1.1. Диполь в однородном электрическом поле

При внесении электрического диполя в однородное внешнее электрическое поле на каждый из его зарядов со стороны поля будут действовать равные по величине, но противоположные по направлению силы:

.

Силы создают вращающий момент:

или , (3.4)

который будет стремиться повернуть диполь так, чтобы его электрический дипольный момент был направлен по направлению внешнего электрического поля (рис. 3.2).

3.1.2. Диполь в неоднородном внешнем электрическом поле

Если диполь помещен в неоднородное внешнее электрическое поле, то силы, действующие на заряды q₊ и q_—, не равны по величине и направлению, так как напряженность электрического поля в точках расположения зарядов не одинакова по величине, отличается на величину

, (3.5)

В этом случае на отрицательный заряд действует сила

.

На положительный заряд действует сила

.

Результирующая сила, действующая на диполь,

(3.6)

Под действием этой силы диполь будет либо втягиваться в область более сильного поля (), либо выталкиваться из него () (рис. 3.4).

Такое же действие оказывает электрическое поле на молекулы диэлектрика.

3.2. Свободные и связанные (поляризационные) заряды в диэлектриках. Поляризация диэлектриков. Вектор поляризации (поляризованность)

Процесс «появления» зарядов на диэлектриках во внешнем электрическом поле называют поляризацией диэлектрика. «Появившиеся» заряды называют связанными (поляризационными).

Различные вещества поляризуются по-разному в зависимости от их строения. Наиболее часто встречаются следующие виды поляризации диэлектриков:

а) деформационная поляризация – это поляризация диэлектриков, при которой у атомов возникает (индуцируется) дипольный момент за счет деформации электронных орбит. Наблюдается у диэлектриков, состоящих из неполярных молекул у веществ, молекулы которых имеют симметричное строение (N₂, H₂, O₂, CO_2, CH₄);

б) ориентационная, или дипольная поляризация, которая заключается в ориентации имеющихся дипольных моментов молекул по направлению электрического поля. Естественно, что тепловое движение препятствует полной ориентации молекул, но в результате совместного действия обоих факторов (электрического поля и теплового движения) возникает преимущественная ориентация дипольных моментов по полю. Ориентация тем сильнее, чем больше напряженность электрического поля и ниже температура. Она характерна для диэлектриков, состоящих из полярных молекул веществ, молекулы которых имеют асимметричное строение, т. е. центры «тяжести» положительных и отрицательных зарядов не совпадают. К таким веществам, например, относятся H₂O, NH₃, SO₂, CO;

При помещении диэлектрика во внешнее электрическое поле он поляризуется, т.е. приобретает отличный от нуля электрический дипольный момент:

, (3.7)

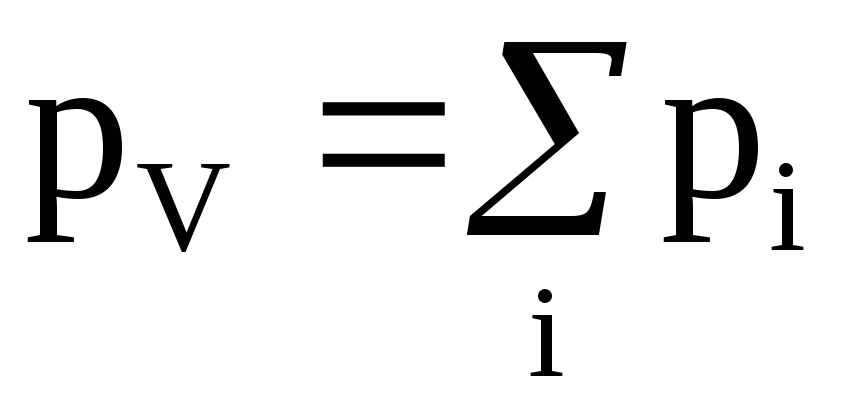
где p_i – дипольный момент одной молекулы.

Для количественной характеристики поляризации диэлектриков вводится в рассмотрение физическая величина, численно равная электрическому дипольному моменту единицы объема диэлектрика:

. (3.8)

Эта величина называется вектором поляризации, или поляризованностью. Если поле или диэлектрик однородны, то вектор поляризации одинаков по всему объему. Такую поляризацию называют однородной. Если эти условия не выполняются, то поляризацию называют неоднородной.

У большинства диэлектриков, кроме так называемых сегнетоэлектриков, вектор поляризации пропорционален напряженности внешнего электрического поля:

, (3.9)

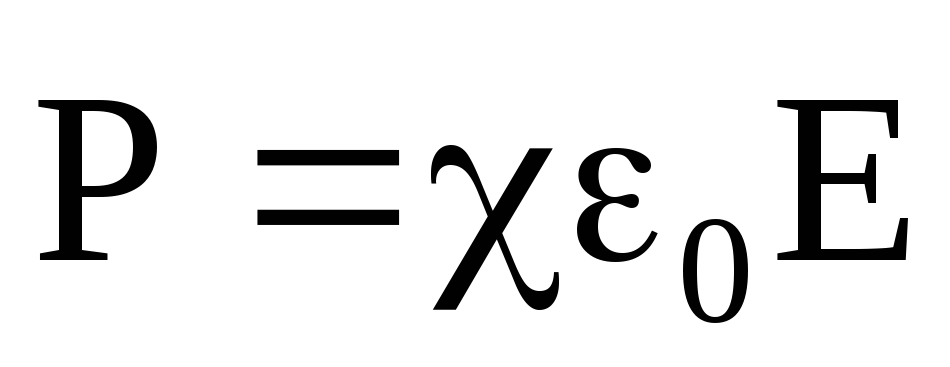
где  – диэлектрическая восприимчивость вещества, не зависящая от напряженности внешнего электрического поля.

Между вектором поляризации P и поверхностной плотностью связанных зарядов  ‘ имеется связь

, (3.10)

т. е. поверхностная плотность связанных зарядов равна нормальной составляющей вектора поляризации в данной точке поверхности диэлектрика.

Внутри диэлектрика в этом случае существует результирующее электрическое поле с напряженностью

, (3.14)

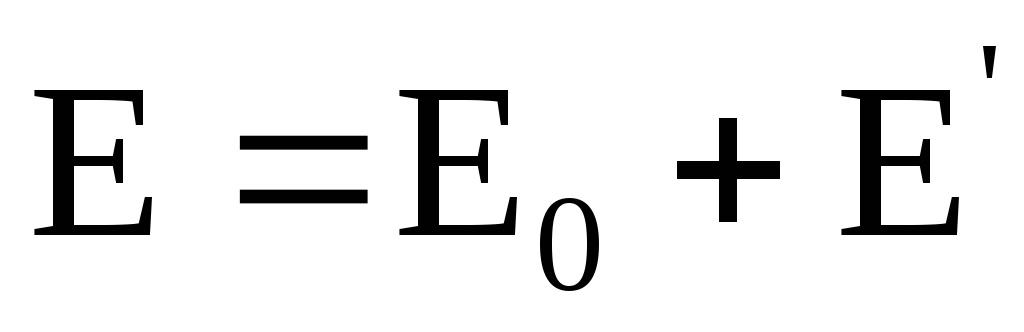
где – напряженность внешнего электрического поля;

–напряженность электрического поля связанных зарядов.

. (3.15)

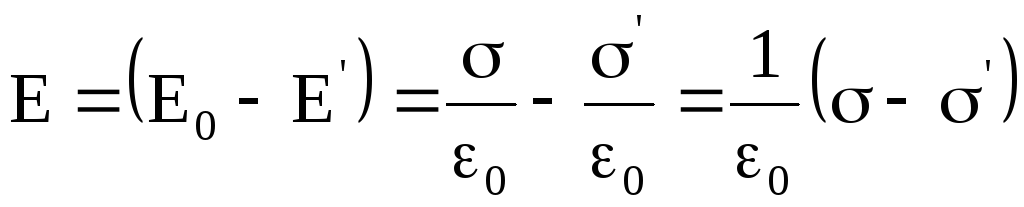
Вне диэлектрика напряженность внешнего поля равна напряженности результирующего электрического поля.

Так как поле перпендикулярно граням пластины и плоскостям, то E_n = E, а с учетом того, что , выражение (3.15) можно переписать так:

. (3.16)

Из формулы (3.16) имеем

,

,

. (3.17)

Следовательно, относительная диэлектрическая проницаемость среды показывает, во сколько раз электрическое поле ослабевает за счет диэлектрика.

Индукция электрического поля D внутри диэлектрика и вне диэлектрика одинакова, т.к. при умножении 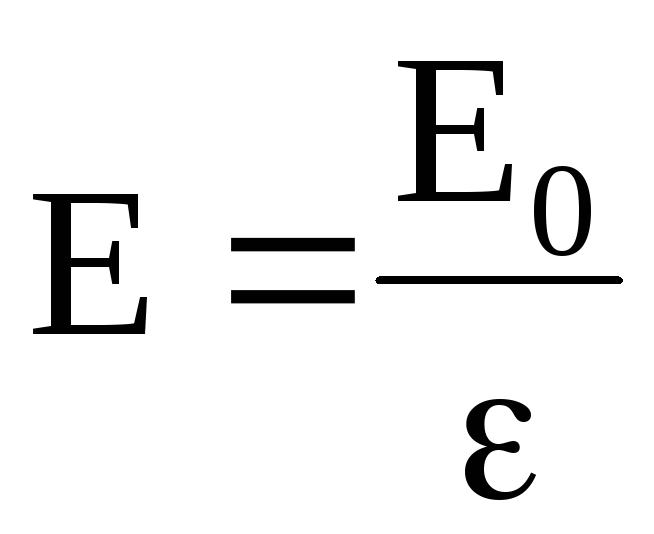на₀ имеем

, или , (3.18)

где D = ₀E – индукция (электрическое смещение) электрического поля внутри диэлектрика;

D_o = ₀E – индукция (электрическое смещение) электрического поля вне диэлектрика.

Таким образом, индукция электрического поля в диэлектрике изменяет свое направление, но не изменяет свою величину, в то время как напряженность электрического поля E  E_o. Полученный результат справедлив для любых электрических полей.

Следовательно, на границе раздела двух сред происходит изменение вектора напряженности электрического поля E (уменьшается число силовых линий вектора E), а вектор индукции электрического поля не изменяется (изменяется лишь вид силовых линий вектора D). Отсюда вывод: поток вектора индукции электрического поля через любую замкнутую поверхность остается величиной постоянной.

Для потока вектора индукции электрического поля D справедлива теорема Остроградского-Гаусса: поток вектора индукции электрического поля через любую замкнутую поверхность равен алгебраической сумме электрических зарядов, заключенных внутри этой замкнутой поверхности.

Математически эту теорему можно записать так:

. (3.19)

Источник

Электрический диполь

Вы будете перенаправлены на Автор24

Что такое электрический диполь

Электрическим диполем называется система из двух точечных зарядов, величина которых одинакова, но противоположна по знаку, при чем, эти точечные заряды разнесены на небольшое расстояние друг от друга. Вектор, соединяющий отрицательный заряд с положительным (направление от минуса к плюсу), называется плечом диполя.

Тогда векторная величина, равная:

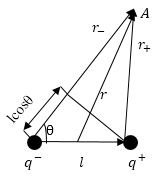
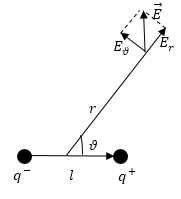
Электрическое поле диполя складывается из напряжённостей зарядов, которые составляют диполь. Так как плечо диполя мало, поэтому можно считать, что оно много меньше, чем расстояние до точек, в которых рассчитывается напряженность поля. Найдем потенциал диполя. В точке А (рис.1) формула для потенциала будет иметь вид:

При этом местоположение точки A можно характеризовать вектором$\overrightarrow<\ r>$ с началом в любой точке диполя, ввиду малых геометрических размеров диполя. В таком случае формулу (2) можно записать в виде:

запишем формулу для напряженности поля диполя, которая будет иметь вид:

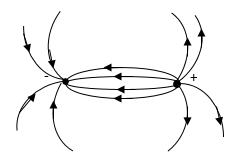
Согласно формуле (6) напряженность поля диполя убывает быстрее, чем напряженность кулоновского поля одиночного заряда, пропорционально третьей степени расстояния. Силовые линии электростатического поля около диполя изображены на рис. 2.

Модуль вектора сопряженности

В таком случае модуль вектора напряженности равен:

Вычисление момента сил

В однородном поле сила, которая действует на диполь со стороны поля ($\overrightarrow$), равна нулю, так как к зарядам приложены одинаковые по модулю и противоположные по направлению силы:

Момент этих сил равен:

Если поле не однородно, то сила (сумма сил действующих на положительный и отрицательный заряд) не равна нулю.$\ \overrightarrow=<\overrightarrow>_++<\overrightarrow>_-\ne 0$. В этом случае сила равна:

В том случае, если мы имеем дело с точечным диполем (плечо диполя очень мало), то сила, действующая на диполь, может быть записана как:

или, что то же самое, но короче:

Задание: Ответьте на вопрос: может ли точечный заряд двигаться с постоянной скоростью вокруг неподвижного точечного диполя?

Напряженность поля, которое создает диполь в точке А (где помещен заряд q) равна:

Тогда силу с которой поле диполя действует на заряд, который помещен в точку А найдем как:

\[F=Q\cdot E\ \left(2.3\right).\]

В результате получаем:

Источник

Диполь в однородном и неоднородном электрических полях

Если диполь поместить в однородное электрическое поле, образующие диполь заряды +q и –q окажутся под действием равных по величине, но противоположных по направлению сил и .

Эти силы образуют пару, плечо которой равно l·sina, т.е. зависит от ориентации диполя относительно поля. Модуль каждой из сил равен q×E. Умножив его на плечо, получим величину момента пары сил, действующей на диполь:

, (14.1)

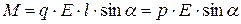
где р – электрический момент диполя.

Формулу (14.1) можно записать в векторном виде:

. (14.2)

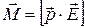
Вращающий момент 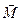стремится повернуть диполь так, чтобы его дипольный момент установился по направлению поля.

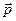
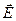
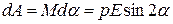
Чтобы увеличить угол между векторами и на 2a, нужно совершить против работу сил, действующих на диполь в электрическом поле:

.

Эта работа идет на увеличение потенциальной энергии W, которой обладает диполь в электрическом поле:

. (14.3)

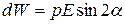
Интегрируя (14.3) получим выражение для энергии диполя в электрическом поле:

.

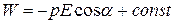
Наконец, полагая const равной нулю, получаем

. (14.4)

В неоднородном поле силы, действующие на заряды диполя, не одинаковые по величине. При малых размерах диполя силы и можно считать коллинеарными. Предположим, что поле быстрее всего изменяется в направлении х, совпадающем с направлением в том месте, где расположен диполь. Положительный заряд диполя смещен относительно отрицательного в направлении х на величину .

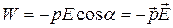
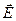
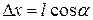
Поэтому напряженность поля в точках, где помещаются заряды, отличается на .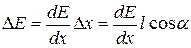

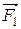
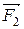
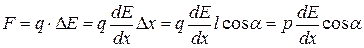
Следовательно, результирующая + сил, действующих на диполь, будет отлична от нуля. Проекция этой результирующей на ось х, очевидно равна:

. (14.5)

Таким образом, в неоднородном поле на диполь кроме вращательного момента (14.2) действует сила (14.5), под действием которой диполь либо втягивается в область более сильного поля (угол a острый), либо выталкивается из нее (угол a тупой).

Дата добавления: 2016-01-29 ; просмотров: 1021 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник